ลำดับ Farey และ วงกลม Ford

Monday, February 25, 2013, 06:44 PM

ปีที่แล้วเล่น Project Euler ไปได้หลายข้อ แล้วก็สะดุดตากับข้อที่น่าสนใจ เลยเอาไปปรึกษาป้ามัลและขยายผลต่อจนได้เรื่องนี้ไปใช้ในวิชาสัมมนา

อธิบายสั้นๆ คือลำดับ Farey เป็นลำดับของเศษส่วนอย่างต่ำตั้งแต่ $\frac{0}{1}$ ไปจนถึง $\frac{1}{1}$ เพราะฉะนั้นตัวเลขอย่าง $\frac{2}{4}$ จึงไม่นับ (หรือถ้าจะนับ ก็ทำให้มันเป็น $\frac{1}{2}$ ก่อน)

อย่างไรก็ดี ถ้านิยามอย่างนี้เราจะมีปัญหาว่าลำดับ Farey มันดันเป็นลำดับอนันต์ซะหนิ ดังนั้นเลยเพิ่มข้อจำกัดไปว่า ลำดับ Farey อันดับ $n$ จะบรรจุเศษส่วนอย่างต่ำ ที่ตัวส่วนมีค่าน้อยกว่าเท่ากับ $n$ เท่านั้น

พอมันเป็นลำดับจำกัดแล้ว ก็สามารถเพิ่มข้อกำหนดสุดท้ายได้ว่า สมาชิกแต่ละตัวในลำดับนี้ ต้องเรียงค่าจากน้อยไปมากด้วย

ส่วนวงกลม Ford ก็เป็นวงกลมที่นำเอาลำดับ Farey ไปวาดแสดงผลได้อย่างสวยงาม 😉

ไม่ต้องกลัวว่าเป็นภาษาคณิตศาสตร์แล้วจะเข้าใจยาก เพราะมีโปรแกรมที่เขียนด้วย Python ให้ไปแกะโค้ดเล่นกันด้วย

ลำดับ Farey

นิยาม 1 ลำดับ Farey อันดับ $n$ เรียกย่อว่า $F_n$ คือลำดับของเศษส่วนอย่างต่ำในช่วง $[0, 1]$ ซึ่งตัวส่วนนั้นมีค่าน้อยกว่าเท่ากับ $n$ และสมาชิกแต่ละตัวเรียงลำดับจากน้อยไปมาก

ตัวอย่าง

\[\begin{align} F_1 &= \left\lbrace \frac01, \frac11 \right\rbrace \\ F_2 &= \left\lbrace \frac01, \frac12, \frac11 \right\rbrace \\ F_3 &= \left\lbrace \frac01, \frac13, \frac12, \frac23, \frac11 \right\rbrace \\ F_4 &= \left\lbrace \frac01, \frac14, \frac13, \frac12, \frac23, \frac34, \frac11 \right\rbrace \\ F_5 &= \left\lbrace \frac01, \frac15, \frac14, \frac13, \frac25, \frac12, \frac35, \frac23, \frac34, \frac45, \frac11 \right\rbrace \\ F_6 &= \left\lbrace \frac01, \frac16, \frac15, \frac14, \frac13, \frac25, \frac12, \frac35, \frac23, \frac34, \frac45, \frac56, \frac11 \right\rbrace \\ F_7 &= \left\lbrace \frac01, \frac17, \frac16, \frac15, \frac14, \frac27, \frac13, \frac25, \frac37, \frac12, \frac47, \frac35, \frac23, \frac57, \frac34, \frac45, \frac56, \frac67, \frac11 \right\rbrace \\ F_8 &= \left\lbrace \frac01, \frac18, \frac17, \frac16, \frac15, \frac14, \frac27, \frac13, \frac38, \frac25, \frac37, \frac12, \frac47, \frac35, \frac58, \frac23, \frac57, \frac34, \frac45, \frac56, \frac67, \frac78, \frac11\right\rbrace \end{align}\]

สมบัติ 1.1 $F_n$ จะบรรจุสมาชิกทุกตัวจาก $F_k$ สำหรับทุกๆ $k \le n$

สมบัติ 1.2 สมาชิกที่เพิ่มเข้ามาใน $F_n$ จาก $F_{n−1}$ คือ $\lbrace a/n \mid 0 < a < n, \gcd(a, n) = 1 \rbrace$

สมบัติ 1.3 ให้ $\abs{F_n}$ แทนจำนวนสมาชิกของ $F_n$ จะได้ว่า $\abs{F_n} = \abs{F_{n-1}} + \phi(n)$

สมบัติ 1.4 จาก $\abs{F_1} = 2$ ดังนั้น $\abs{F_n} = 1 + \sum\limits_{k=1}^n \phi(k)$

สมบัติ 1.5 สมาชิกตัวที่สองของ $F_n$ มีค่าเท่ากับ $1/n$

ออยเลอร์ทอเทียนต์ (Euler’s totient) สัญลักษณ์ $\phi(n)$ คือฟังก์ชันแสดงจำนวนนับในช่วง $[1, n]$ ที่เป็นจำนวนเฉพาะสัมพัทธ์กับ $n$ มีสูตรทั่วไปคือ
\[\begin{align} \phi(1) &= 1 \\ \phi(p^kq) &= p^{k-1}(p - 1)\phi(q), \quad\quad \gcd(p^k, q) = 1 \end{align}\]

ขั้นตอนวิธี 1 การสร้างลำดับ Farey ด้วยการไล่ทุกเศษส่วนที่เป็นไปได้ แล้วเก็บเฉพาะเศษส่วนอย่างต่ำ

จากสมบัติ 1.2 สามารถเขียนฟังก์ช้นในภาษา Python สำหรับหา $F_n$ ได้ดังนี้

def farey(n):
    sequence = [Fraction(0), Fraction(1)]
    for b in range(1, n+1):
        for a in range(1, b):
            if gcd(a, b) == 1:
                sequence += [Fraction(a, b)]
    return sorted(sequence)

นิยาม 2 ค่า mediant มีค่าเท่ากับ $\frac{a+c}{b+d}$ สำหรับเศษส่วนอย่างต่ำ $\frac{a}{b}, \frac{c}{d}$

ทฤษฎีบท 2.1 ถ้า $\frac{a}{b} < \frac{c}{d}$ แล้ว $\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}$

พิสูจน์ จาก $\frac{a}{b} < \frac{c}{d}$ จะได้ว่า

\[\begin{align} \frac{ad}{b} &< c \\ a + \frac{ad}{b} &< a + c \\ \frac{a(b+d)}{b} &< a + c \\ \frac{a}{b} &< \frac{a+c}{b+d} \end{align}\]

\[\begin{align} a &< \frac{cb}{d} \\ a + c &< \frac{cb}{d} + c \\ a + c &< \frac{c(b+d)}{d} \\ \frac{a+c}{b+d} &< \frac{c}{d} \end{align}\]

ทฤษฎีบท 2.2 พจน์ใดๆ ใน $F_n$ จะเป็น mediant ของสองพจน์ที่อยู่ก่อนและหลัง หรือเป็นพจน์ขอบของ $F_n$

พิสูจน์ ให้ $\frac{a}{b}$ เป็นสมาชิกของ $F_n$ ใดๆ

กรณีแรก ถ้า $\frac{a}{b} = \frac01$ หรือ $\frac{a}{b} = \frac11$ แล้ว $\frac{a}{b}$ จะเป็นพจน์ขอบของ $F_n$
กรณีสอง จากอัตลักษณ์ของเบซู ได้สมการ $ax - bz = 1$ ที่สามารถหาคำตอบ $x,z$ ซึ่ง $0 \le z < x$ พิจารณา $x < b, z < a$ จะเห็นว่า $\frac{z}{x}, \frac{a-z}{b-x}$ อยู่ใน $F_k$ ที่ $k \le n$ และทำให้ $\frac{a}{b}$ เป็น mediant ของ $\frac{z}{x}, \frac{a-z}{b-x}$ ใน $F_n$

อัตลักษณ์ของเบซู (Bézout’s identity) กล่าวว่า สมการ $ax + by = \gcd(a, b)$ มีคำตอบ $x, y \in \mathbb{Z}$ หลายค่า (หาคำตอบได้โดยใช้ Extended Euclidean Algorithm) เนื่องจากในที่นี้ $\gcd(a,b) = 1$ และ $0 \le a < b$ สนใจคำตอบที่ $x > 0$ และ $y \le 0$ ให้ $z = -y$ จะได้ $az − bz = 1$ ที่ $0 \le z < x$

ทฤษฎีบท 2.3 สำหรับ $\frac{a}{b}, \frac{c}{d}$ ที่อยู่ติดกันใน $F_n$ แล้ว $bc - ad = 1$

พิสูจน์ เลือก 3 พจน์ติดกันใน $F_n$ คือ $\frac{a}{b}, \frac{c}{d}, \frac{e}{f}$ จะได้ว่า $bc - ad = de - cf$ เนื่องจากสมการนี้จริงสำหรับทุกๆ 3 พจน์ใดๆ ที่ติดกันใน $F_n$ ดังนั้น $1 = 1\cdot1 - n\cdot0 = \dots = bc - ad = de - cf = \dots$

ทฤษฎีบท 2.4 สำหรับ $\frac{a}{b},\frac{c}{d}$ ที่อยู่ติดกันใน $F_n$ แล้ว $\gcd(a+c,b+d) = 1$

พิสูจน์ เพราะ $1 = bc - ad = (a+c)b - (b+d)a$ หรือสามารถเขียนได้อีกอย่างว่า $1 = (a+c)x-(b+d)z$ โดยอัตลักษณ์ของเบซู จะได้ว่า $\gcd(a+c,b+d)=1$

ขั้นตอนวิธี 2 การสร้างลำดับ Farey ด้วยการสร้างลำดับ Farey (ด้วยการสร้างลำดับ Farey (…))

อย่างไรก็ตาม วิธีที่ 1 เป็นการหาสมาชิกทุกตัวแล้วนำมาเรียงลำดับ แต่วิธีที่ 2 นั้น จะเป็นการหาสมาชิกของลำดับไปพร้อมๆ กับการกำหนดตำแหน่งในลำดับ ดังนั้นจะหา $F_n$ โดยอาศัยทฤษฎีบทที่ 2.2 และ 2.4

def farey(n):
    if n == 1:
        return [Fraction(0), Fraction(1)]
    sequence = []
    for g in farey(n-1):
        if sequence:
            b = f.denominator + g.denominator
            if b == n:
                a = f.numerator + g.numerator
                sequence += [Fraction(a, b)]
        f = g
        sequence += [g]
    return sequence

ทฤษฎีบท 2.5 สำหรับ $\frac{a}{b}, \frac{c}{d}$ ที่อยู่ติดกันใน $F_n$ จะได้ว่าพจน์ถัดไปคือ $\frac{kc-a}{kd-b}$ โดยที่ $k = \left\lfloor \frac{n+b}{d} \right\rfloor$

พิสูจน์ ให้พจน์ถัดไปที่ต้องการหาคือ $\frac{e}{f}$ จะได้ว่า $\frac{c}{d} = \frac{a+e}{b+f}$ แต่เนื่องจาก $\gcd(a+e,b+f) = k \ge 1$ ดังนั้น $kc = a + e$ และ $kd = b + f$ โดยที่ $kd - b = f \le n$ และทำให้ได้ว่า $k = \left\lfloor \frac{n+b}{d} \right\rfloor \le \frac{n+b}{d}$

ขั้นตอนวิธี 3 การสร้างลำดับ Farey ด้วยการเพิ่มสมาชิกลงในลำดับไปเรื่อยๆ โดยใช้ข้อมูลจากสมาชิกที่มี

อาศัยสมบัติ 1.5 และทฤษฎีบทที่ 2.5 การสร้าง $F_n$ ด้วยวิธีนี้ เพียงแต่ทราบ 2 เทอมแรกในลำดับก็สามารถหาสมาชิกที่เหลือของลำดับได้

def farey(n):
    sequence = [f, g] = [Fraction(0), Fraction(1, n)]
    while g < 1:
        k = (n + f.denominator) // g.denominator
        a = k * g.numerator - f.numerator
        b = k * g.denominator - f.denominator
        f, g = g, Fraction(a, b)
        sequence += [g]
    return sequence

วงกลม Ford

นิยาม 3 สำหรับเศษส่วนอย่างต่ำ $p/q$ นิยามวงกลม Ford ด้วยสัญลักษณ์ $C(p,q)$ คือวงกลมที่มีจุดศูนย์กลางที่ $\left( \frac{p}{q}, \frac1{2q^2} \right)$ และมีรัศมี $\frac1{2q^2}$

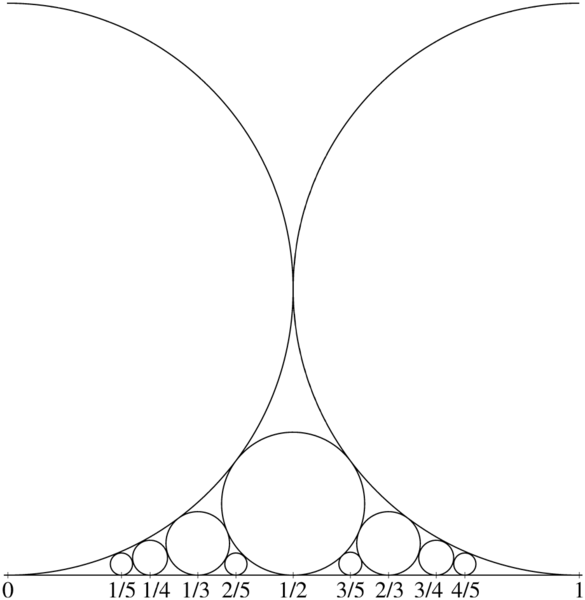
ภาพ 1: วงกลม Ford ที่สร้างจากเศษส่วนของลำดับ Farey อันดับ 5

ทฤษฎีบท 3.1 ไม่มีวงกลม Ford คู่ใดเลยที่ซ้อนกัน

พิสูจน์ ให้ $R$ แทนระยะห่างระหว่างจุดศูนย์กลางของ $C(a,b), C(c,d)$ และให้ $r_{C(a,b)}, r_{C(c,d)}$ แทนรัศมีของวงกลมทั้งสองตามลำดับ

\[\begin{align} R &= \sqrt{ \left( \frac{c}{d}-\frac{a}{b} \right)^2 + \left( \frac1{2d^2} - \frac1{2b^2} \right)^2 } \\ &= \frac1{2b^2d^2} \sqrt{4b^2d^2(bc-ad)^2 + (b^2-d^2)^2} \\ &\ge \frac1{2b^2d^2} \sqrt{4b^2d^2 + (b^2-d^2)^2} \\ &= \frac1{2b^2} + \frac1{2d^2} \\ &= r_{C(a,b)} + r_{C(c,d)} \end{align}\]

เพราะระยะห่างจากศูนย์กลางของสองวงกลม มีค่ามากกว่ารัศมีรวมกัน ดังนั้นจึงไม่มีวงกลม Ford คู่ใดซ้อนกัน

ทฤษฎีบท 3.2 วงกลม $C(a,b), C(c,d)$ ที่สัมผัสกันและ $\frac{a}{b} < \frac{d}{c}$ มีจุดสัมผัสที่ $\left( \frac{a}{b} + \frac1{b^2+d^2}\frac{d}{b}, \frac1{b^2+d^2} \right)$

พิสูจน์ จากสูตร $(x,y) = \left( \frac{mx_2+nx_1}{m+n}, \frac{my_2+ny_1}{m+n} \right)$

วงกลม $C(a,b)$ มีจุดศูนย์กลางอยู่ที่ $(x_1,y_1) = (\frac{a}{b}, \frac1{2b^2})$ และ $m = r_1 = \frac1{2b^2}$
วงกลม $C(c,d)$ มีจุดศูนย์กลางอยู่ที่ $(x_2,y_2) = (\frac{c}{d}, \frac1{2d^2})$ และ $n = r_2 = \frac1{2d^2}$

ดังนั้น จุดสัมผัสของวงกลม $C(a,b), C(c,d)$ จะอยู่ที่

\[\begin{align} (x,y) &= \left( \frac{r_1x_2+r_2x_1}{r_1+r_2}, \frac{r_1y_2+r_2y_1}{r_1+r_2} \right) \\ &= \left( \frac{r_2}{r_1+r_2}\frac{a}{b} + \frac{r_1}{r_1+r_2}\frac{c}{d}, \frac{r_1r_2+r_2r_1}{r_1+r_2} \right) \\ &= \left( \frac{r_1+r_2}{r_1+r_2}\frac{a}{b} + \frac{r_1}{r_1+r_2}(\frac{c}{d}-\frac{a}{b}), \frac{2r_1r_2}{r_1+r_2} \right) \\ &= \left( \frac{a}{b} + \frac1{2b^2}\frac{2b^2d^2}{b^2+d^2}\frac{bc-ad}{bd}, 2\frac1{2b^2}\frac1{2d^2}\frac{2b^2d^2}{b^2+d^2} \right) \\ &= \left( \frac{a}{b} + \frac1{b^2+d^2}\frac{d}{b}, \frac1{b^2+d^2} \right) \end{align}\]

ทฤษฎีบท 3.3 $C(a+c, b+d)$ จะเป็นวงกลม Ford ที่ใหญ่ที่สุดระหว่างวงกลม Ford $C(a,b), C(c,d)$ ที่สัมผัสกัน

พิสูจน์ สมมติให้ $C(a+c, b+d)$ ไม่ใช่วงกลม Ford ที่ใหญ่ที่สุด ดังนั้น จะมี $C(p,q)$ ที่ $q < b + d$ ซึ่งเป็นวงกลม Ford ที่ใหญ่ที่สุด เนื่องจาก $C(p,q)$ อยู่ระหว่าง $C(a,b), C(c,d)$ ดังนั้น $\frac{a}{b} < \frac{p}{q} < \frac{c}{d}$ แต่เพราะ $\gcd(a+c,b+d) = 1$ จากทฤษฎีบท 2.4 ดังนั้น $q \ge b + d$ เกิดเป็นข้อขัดแย้ง เพราะ $q < b + d$ และ $q \ge b + d$ พร้อมกันไม่ได้ ดังนั้น $C(a+c,b+d)$ จะเป็นวงกลม Ford ที่ใหญ่ที่สุดระหว่าง $C(a,b), C(c,d)$