อัลกอริทึมเส้นกวาดเพื่อหาส่วนของเส้นตรงที่ตัดกัน
ตอนก่อนเราได้พิจารณาการตัดกันของส่วนของเส้นตรงหนึ่งคู่ไปแล้ว ถึงแม้อัลกอริทึมจะมีการคำนวณที่ค่อนข้างซับซ้อน แต่เพราะมันมีจำนวนขั้นตอนวิธีที่คงที่ไม่ว่าข้อมูลนำเข้าจะเป็นอย่างไร (เพราะเราดันกำหนดให้ข้อมูลนำเข้าที่เป็นไปได้มีแค่ส่วนของเส้นตรงเพียงสองเส้น) ดังนั้นเราอาจมองง่ายๆ ว่าอัลกอริทึมดังกล่าวกินเวลาเป็น $O(1)$ ได้เลย
คำถามที่น่าสนใจกว่าก็คือ ถ้าข้อมูลนำเข้าไม่ได้เป็นส่วนของเส้นตรงแค่เพียงสองเส้น แต่มีมากถึง $n$ เส้นหละ ความเร็วในการคำนวณจะเป็นเท่าไหร่? สามารถทำได้ดีกว่า $O(n^2)$ ที่เป็นการตรวจสอบทุกรูปแบบการจับคู่ส่วนของเส้นตรงทุกวิธีได้หรือไม่?
อัลกอริทึมที่จะมาตอบปัญหานี้คืออัลกอริทึมแบบเส้นกวาด ซึ่งมีหัวใจการทำงานอยู่ที่การสร้างสมมติเส้นในจินตนาการขึ้นมา (หรืออาจเป็นระนาบหากพิจารณาในมิติที่สูงขึ้น) แล้วเลื่อนเส้นนั้นผ่านชุดข้อมูลที่สนใจ พร้อมสังเกตเหตุการณ์สำคัญว่าส่งผลอย่างไรบ้าง
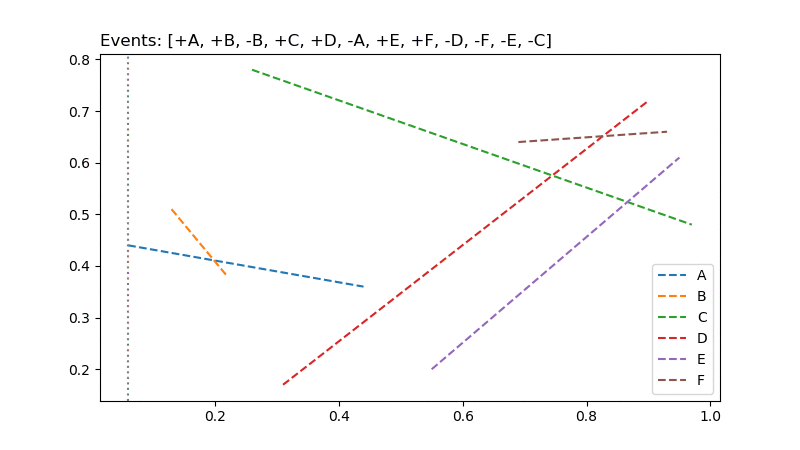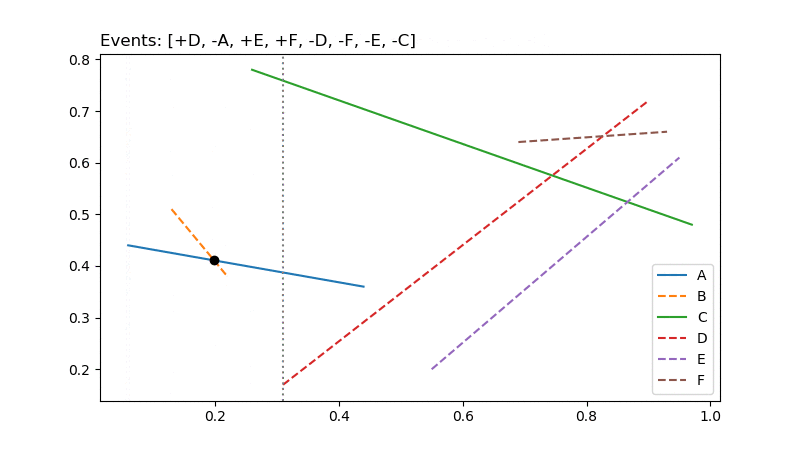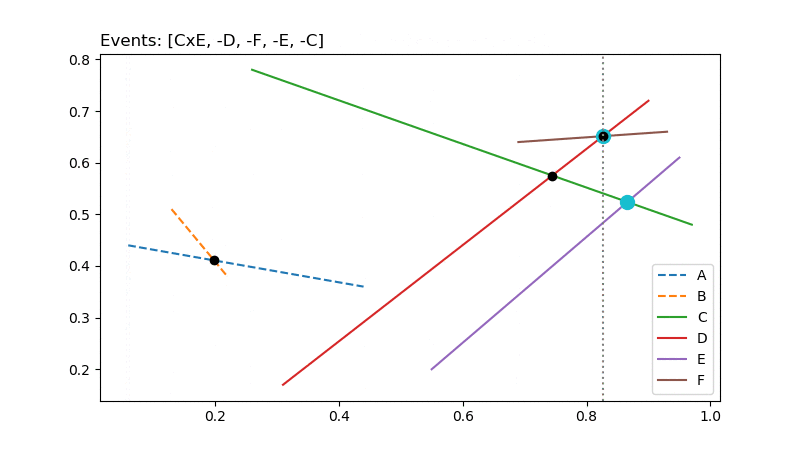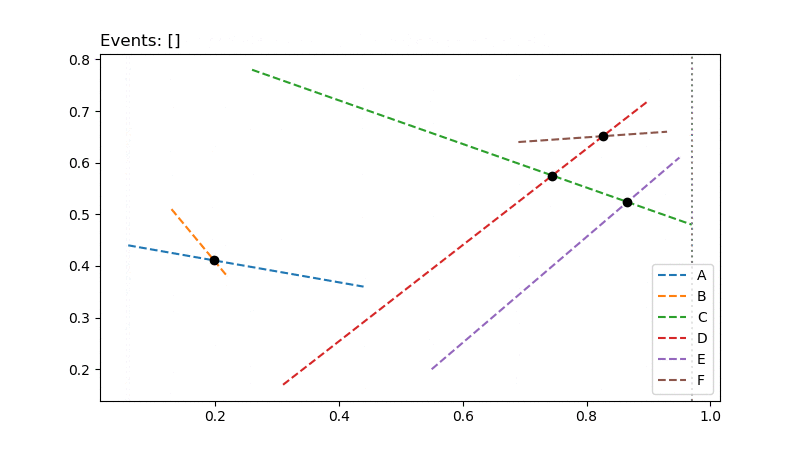
อนิเมชันอัลกอริทึมเส้นกวาดเพื่อหาการตัดกันของส่วนของเส้นตรง1
สำหรับอัลกอริทึมเส้นกวาดเพื่อหาการตัดกันของส่วนของเส้นตรง มีหลักการทำงานง่ายๆ โดยเริ่มจากสร้างเส้นกวาดที่ขนานกับแกน Y และอยู่ทางซ้ายสุดก่อนหน้าส่วนของเส้นตรงทั้งหมด ซึ่งเส้นกวาดนี้จะใช้จดจำสถานะว่าขณะนั้นกำลังมองเห็นส่วนของเส้นตรงใดอยู่ (เรียงลำดับจากล่างขึ้นบน) หลังจากนั้นจึงเลื่อนเส้นกวาดดังกล่าวไปทางขวาเรื่อยๆ จนเจอเหตุการณ์ที่น่าสนใจดังนี้ (เหตุการณ์ในตอนเริ่มต้น จะประกอบด้วยจุดปลายของส่วนของเส้นตรงทั้งหมด เรียงลำดับจากซ้ายไปขวา)
- เมื่อถึงจุดเริ่มของส่วนของเส้นตรงใหม่:
- แทรกส่วนของเส้นตรงเส้นใหม่ลงไปในสถานะ
- คำนวณจุดตัดของส่วนของเส้นตรงใหม่กับส่วนของเส้นตรงที่อยู่ติดกันในสถานะ แล้วเพิ่มลงในเหตุการณ์
- เมื่อถึงจุดจบของส่วนของเส้นตรงเดิม:
- ลบส่วนของเส้นตรงนั้นทิ้งไป
- คำนวณจุดตัดระหว่างส่วนของเส้นตรงที่อยู่ก่อนหน้าและตามหลังส่วนของเส้นตรงที่เพิ่งลบไป แล้วเพิ่มลงในเหตุการณ์
- เมื่อถึงจุดตัดระหว่างส่วนของเส้นตรง:
- รายงานจุดตัดที่พบ
- สลับตำแหน่งในสถานะของส่วนของเส้นตรงที่ตัดกัน
- คำนวณจุดตัดของส่วนของเส้นตรงที่ติดกับส่วนของเส้นตรงที่เพิ่งสลับที่ไป แล้วเพิ่มลงในเหตุการณ์
สังเกตว่าที่ตำแหน่งอื่นๆ ที่อยู่นอกเหนือเหตุการณ์ที่น่าสนใจ ไม่ส่งผลกระทบต่อสถานะและเหตุการณ์เลย
หากเลือกใช้โครงสร้างข้อมูลที่มีประสิทธิภาพเหมาะสมในการเก็บสถานะและเหตุการณ์ (เช่น ต้นไม้ค้นหาแบบทวิภาค) เราจะสามารถเพิ่ม ลบ และค้นหาข้อมูลได้ในเวลา $O(\log n)$ ซึ่งนี่คือความเร็วในการทำงานแต่ละครั้งที่เส้นกวาดเลื่อนไปพบกับเหตุการณ์ที่สนใจ เนื่องจากเรามีเหตุการณ์ที่สนใจเริ่มต้นอยู่ $2n$ เหตุการณ์ (จุดเริ่มและจุดจบของส่วนของเส้นตรง) และมีเหตุการณ์เพิ่มมาอีก $k$ เหตุการณ์เมื่อส่วนของเส้นตรงใดๆ เกิดการตัดกัน ดังนั้นเวลารวมทั้งหมดของอัลกอริทึมจึงกลายเป็น $O((n+k)\log n)$ … พอเห็นแบบนี้แล้วก็แน่นอนว่า ความเร็วของอัลกอริทึมนี้เป็นแบบขึ้นกับขนาดคำตอบ
และเมื่อวิเคราะห์ต่อไปจะพบว่า ส่วนของเส้นตรงใดๆ ตัดกับส่วนของเส้นตรงอื่นได้มากที่สุด $n-1$ ครั้ง ดังนั้นจึงมีจุดตัดทั้งหมดได้มากที่สุดเป็น $k=O(n^2)$ หรือกลับกลายเป็นว่าอัลกอริทึมนี้จะใช้เวลามากกว่าการทดสอบทุกคู่ส่วนของเส้นตรงเสียอีก แต่ข้อมูลในโลกจริงส่วนของเส้นตรงมักมีการกระจายตัวอย่างประปราย ไม่ได้ถูกสุ่มกระจายตัดกันมากมายแบบงานศิลป์ของ Jackson Pollock ทำให้โดยทั่วไปแล้ว อัลกอริทึมนี้ไม่ควรใช้เวลาแย่กว่าการทดสอบทุกคู่นั่นเอง
ตัวอย่างข้อมูลนำเข้าที่มีความหนาแน่นเป็นหย่อมๆ แต่ในภาพรวมแล้วยังมีความโปร่งอยู่ ทำให้อัลกอริทึมแบบเส้นกวาดยังคงทำงานได้ดีกว่าอัลกอริทึมแบบทดสอบเส้นตรงทุกคู่2
… อธิบายจบแล้ว แปะโค้ดได้ 😜
from collections import namedtuple
from blist import blist, sortedlist # pip install blist
Point = namedtuple('Point', 'x y')
Segment = namedtuple('Segment', 'p q')
Segment.from_floats = lambda x0, y0, x1, y1: Segment.from_points(Point(x0, y0), Point(x1, y1))
Segment.from_points = lambda p, q: Segment(*sorted([p, q]))
Segment.ccw = lambda self, p: Triangle(p, *self).ccw()
Segment.cut = lambda self, other: self.ccw(other.p) ^ self.ccw(other.q)
Segment.det = lambda self: self.p.x*self.q.y - self.p.y*self.q.x
Segment.dx = lambda self: self.p.x - self.q.x
Segment.dy = lambda self: self.p.y - self.q.y
Pair = namedtuple('Pair', 's t')
Pair.from_segments = lambda s, t: Pair(*sorted([s, t]))
Pair.denominator = lambda self: self.s.dx()*self.t.dy() - self.s.dy()*self.t.dx()
Pair.is_intersect = lambda self: self.s.cut(self.t) and self.t.cut(self.s)
Pair.intersect_coord = ( lambda self:
None if not self.is_intersect() else
Point( (self.s.det()*self.t.dx() - self.s.dx()*self.t.det()) / self.denominator(),
(self.s.det()*self.t.dy() - self.s.dy()*self.t.det()) / self.denominator() ))
Triangle = namedtuple('Triangle', 'u v w')
Triangle.ccw = lambda self: round(self.det(), 9) > 0
Triangle.det = lambda self: ( self.u.x*self.v.y - self.u.y*self.v.x +
self.v.x*self.w.y - self.v.y*self.w.x +
self.w.x*self.u.y - self.w.y*self.u.x )
AddEvent = namedtuple('AddEvent', 'p s t') # dummy 3rd attr
AddEvent.from_segment = lambda s: AddEvent(s.p, s, s)
DelEvent = namedtuple('DelEvent', 'p s t') # dummy 3rd attr
DelEvent.from_segment = lambda s: DelEvent(s.q, s, s)
IntersectEvent = namedtuple('IntersectEvent', 'p s t')
IntersectEvent.from_segments = lambda s, t: IntersectEvent.from_pair(Pair.from_segments(s, t))
IntersectEvent.from_pair = lambda ps: IntersectEvent(ps.intersect_coord(), *ps)
def init_events(segments):
events = sortedlist()
for s in segments:
events.add(AddEvent.from_segment(s))
events.add(DelEvent.from_segment(s))
return events
def add_intersect_event(i, j, status, events):
if 0 <= i < len(status) and 0 <= j < len(status):
intersection = IntersectEvent.from_segments(status[i], status[j])
if ( intersection.p is not None
and intersection not in events
and events[0].p <= intersection.p <= events[-1].p ):
events.add(intersection)
def ccw_bin_search(event, status):
lo = 0
hi = len(status)
while lo < hi:
i = (lo+hi) // 2
if status[i].ccw(event.p):
lo = i + 1
else:
hi = i
return lo
def sweep(segments):
intersections = set()
status = blist()
events = init_events(segments)
while events:
i = ccw_bin_search(events[0], status)
if isinstance(events[0], AddEvent):
status.insert(i, events[0].s)
add_intersect_event(i, i-1, status, events)
add_intersect_event(i, i+1, status, events)
elif isinstance(events[0], DelEvent):
del status[i]
add_intersect_event(i-1, i, status, events)
else:
intersections.add(Pair(events[0].s, events[0].t))
status[i], status[i+1] = status[i+1], status[i]
add_intersect_event(i-1, i-0, status, events)
add_intersect_event(i+1, i+2, status, events)
del events[0]
return intersections
-
สคริปต์ Python สำหรับสร้างอนิเมชัน ↩
-
สคริปต์ Python สำหรับสร้างงานศิลป์ชิ้นนี้ 🤪 ↩

author