ปรกติไม่ได้ตามการแข่งขันโอลิมปิกวิชาการลึกถึงขั้นหยิบโจทย์มาวิเคราะห์ กระทั่งวันก่อน @vacharapat เอาโจทย์โอลิมปิกคณิตศาสตร์ปีนี้มาหลอกถามให้ดูเล่น ตอนแรกกะจะไม่ทำเพราะโจทย์พวกนี้มักจะยากเกินกำลังที่จะคิดออก แต่ไม่รู้ทำไมยิ่งพยายามลืมเท่าไหร่โจทย์มันก็ยิ่งวนเวียนหลอกหลอนในหัวจนนอนไม่หลับ สุดท้ายเลยกลั้นใจลุกขึ้นมาลุยกับมันดูซักตั้ง

Problem 3. There are $4n$ pebbles of weights $1, 2, 3, \dots, 4n$. Each pebble is coloured in one of $n$ colours and there are four pebbles of each colour. Show that we can arrange the pebbles into two piles so that the following two conditions are both satisfied:

• The total weights of both piles are the same.
• Each pile contains two pebbles of each colour.

International Mathematical Olympiad, 2020

โจทย์ขอแค่ให้แสดงซักวิธีที่เป็นไปได้ในการจัดกลุ่มก้อนกรวดให้เป็นไปตามเงื่อนไข ซึ่งเราแอบโกงนิดหน่อยด้วยการเขียนโปรแกรมทุ่นแรงเพื่อดูรูปแบบคำตอบ แม้คำตอบที่เป็นไปได้จะมีมากมายมหาศาล แต่หลังจากมองหารูปแบบไปซักพักก็พบว่ามีอยู่รูปแบบหนึ่งที่ง่ายและเป็นระเบียบสวยงามพอที่จะนำมาอธิบาย

เราเริ่มจากลองมองโจทย์ให้ง่ายลงโดยตัดเงื่อนไขให้เหลือเพียงข้อแรก ซึ่งก็คือแบ่งกรวดเป็น $2$ กอง โดยที่แต่ละกองมีน้ำหนักรวมเท่ากัน สังเกตว่าเรายังสามารถแบ่งได้หลายแบบอยู่ดี แต่เราควรจะแบ่งยังไงให้เป็นระบบเหมาะสมกับโจทย์ข้อนี้หละ?

วิธีหนึ่งที่สวยงามน่าสนใจและเหมาะสม คือ เราจะจับคู่ก้อนกรวดให้เหลือ $2n$ คู่ก่อน โดยที่ทุกคู่มีน้ำหนักรวมเท่ากัน ซึ่งก็คือจับคู่กรวดน้ำหนัก $i$ กับ $4n{+}1{-}i$ เข้าด้วยกัน ดังนั้นกรวดแต่ละคู่ก็จะมีน้ำหนัก $4n{+}1$ นั่นเอง¹ เมื่อแต่ละคู่น้ำหนักเท่ากันแล้ว เราก็ไม่ต้องสนใจน้ำหนักอีก สนใจเพียงแค่หยิบกรวดออกมา $n$ คู่เป็นกองที่หนึ่ง และให้กรวดที่เหลืออีก $n$ คู่เป็นกองที่สอง ก็จะเห็นว่าทั้งสองกองมีน้ำหนักเท่ากันแล้ว

ต่อมาพิจารณาเพิ่มเงื่อนไขข้อที่สองเข้าไป โดยเราจะเริ่มจากจับคู่กรวด $2n$ คู่ตามวิธีข้างต้น สิ่งที่เพิ่มมาคือคราวนี้คือเราสนใจสีของกรวดแต่ละคู่ด้วย ให้กรวดก้อนที่น้ำหนัก $i$ มีสีเป็น $c_i$ จะเห็นว่าหากเราเลือกหยิบกรวดคู่ที่น้ำหนัก $(i,4n{+}1{-}i)$ เราก็จะต้องหยิบกรวดสองสีคือ $(c_i,c_{4n+1-i})$ มาพร้อมกัน

สร้างมัลติกราฟโดยให้แต่ละจุดยอดแทนสีทั้งหมด แล้วลากเส้นเชื่อมโดยเชื่อมจุดยอดทั้งสองสีจากก้อนกรวดแต่ละคู่ ถึงตอนนี้จะเห็นว่ากราฟมีจุดยอด $n$ จุด มีเส้นเชื่อม $2n$ เส้น และแต่ละจุดยอดมีดีกรีเท่ากับ $4$ พอดี

สมมติว่ากราฟที่ได้มีเพียงคอมโพเนนท์เดียว (หากมีหลายคอมโพเนนท์ก็พิจารณาแบบอุปนัยลงไป) เนื่องจากทุกจุดยอดมีดีกรีคู่ เราสามารถหาวงจรออยเลอร์ที่มีขนาด $2n$ ได้ หากเราหยิบเส้นเชื่อมตามทางเดินในวงจรสลับกัน ซึ่งก็คือ ให้เส้นเชื่อมในวงจรตำแหน่งคี่ไปอยู่กลุ่มที่หนึ่ง ในทำนองเดียวกันให้เส้นเชื่อมตำแหน่งคู่ไปอยู่กลุ่มที่สอง จะได้ว่าแต่ละกลุ่มจะมีเส้นเชื่อม $n$ เส้นเท่ากัน เมื่อแปลงเส้นเชื่อมเหล่านั้นกลับเป็นคู่ของก้อนกรวด ก็จะได้ว่าน้ำหนักรวมของกรวดแต่ละกลุ่มมีค่าเท่ากันด้วย

และการหยิบเส้นเชื่อมสลับกันไปแบบนี้ ก็ยังรับประกันด้วยว่าจะแบ่งกลุ่มก้อนกรวดให้มีสีเท่ากันด้วย เพราะเมื่อพิจารณาที่จุดยอดสีใดๆ เนื่องจากจุดยอดมีดีกรีเป็น $4$ เมื่อเดินตามวงจรออยเลอร์ที่คำนวณไว้ จะมีการวิ่งเข้าและวิ่งออกอย่างละ $2$ ครั้ง ซึ่งการวิ่งเข้าและวิ่งออกแต่ละครั้งจะจัดกลุ่มเส้นเชื่อมเป็นกลุ่มที่แตกต่างกันเสมอ ดังนั้นแต่ละจุดยอดจะจัดแบ่งเส้นเชื่อมออกไปเป็นสองกลุ่มเท่ากันพอดี

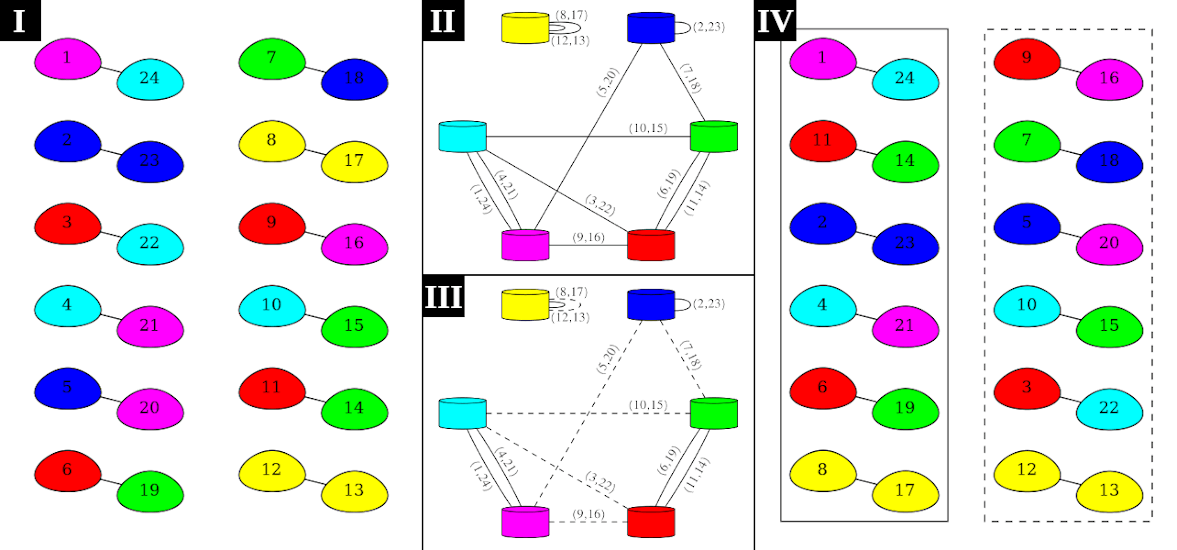
ตัวอย่างเมื่อ $n=6$ เริ่มจากจับคู่ก้อนกรวด แปลงเป็นกราฟเพื่อหาวงจรออยเลอร์ แล้วหยิบเส้นเชื่อมสลับกันเป็นคำตอบ

โอ้ว เป็นโจทย์ที่สนุกอะไรอย่างนี้! เริ่มมาเป็นปัญหาเชิงการจัด ไปยืมเทคนิคจากทฤษฎีจำนวน แล้วแปลงไปจบที่ทฤษฎีกราฟซะได้ แก้เสร็จแล้วยูเรก้ามากๆ 🎉🎉🎉 ขอบคุณพี่ท็อปผู้เปิดโลกคำถามสนุกๆ และเพื่อนร่วมแลปที่มาช่วยขัดเกลาคำตอบให้สมบูรณ์ ณ ที่นี้ด้วย

neizod

author, illustrator

Nonthaphat Wongwattanakij

coauthor