Hacker Cup 2020: น้องเต่าในบ่อน้ำ
โจทย์จากรอบชิงขนะเลิศของ Facebook Hacker Cup ปี 2020 ที่แม้จะไม่ใช่ข้อที่ยากที่สุด แต่ก็มีความน่าสนใจในหลายระดับ (และหากไล่ให้ถูกทางก็จะคิดคำตอบได้ง่ายกว่าที่คิด) ได้แก่ข้อ Pond Precipitation ที่โจทย์ให้แผนที่บ่อน้ำแห่งหนึ่งที่น้องเต่าอาศัยอยู่ แล้วถามหาค่าคาดหวังว่าฝนต้องตกเป็นจำนวนกี่หยดจึงจะทำให้น้องเต่าจมน้ำ โดยคำนึงว่าฝนแต่ละหยดมีโอกาสตกลงยังแต่ละตำแหน่งในบ่อน้ำเท่าเท่ากัน
นั่นก็คือ หากให้ $X$ เป็นตัวแปรสุ่มแทนน้ำฝนหยดที่ทำให้น้องเต่าจมน้ำ โจทย์ให้เราหา
\[E(X) = \sum_{d \in \mathbb{N}} d \cdot P(X=d)\]แปลงปัญหาให้เหมาะสม
แม้ข้อมูลนำเข้าของโจทย์ข้อนี้ (ความกว้างของบ่อน้ำ) จะเล็กเพียง $n=30$ และโจทย์รับประกันว่าฝนตกไม่เกิน $n^2$ หยดก็จะท่วมน้องเต่า แต่หากเลือกใช้ขั้นตอนวิธีแบบทดลองหยดน้ำฝนทุกรูปแบบ จะเห็นว่าความซับซ้อนของขั้นตอนวิธีพุ่งสูงเป็น $O(n^{n^2})$ นั่นหมายความว่ามันไม่มีทางทำงานทันแน่นอน อย่างไรก็ตาม หากใครคุ้นเคยกับการแข่งขันเขียนโปรแกรมที่เน้นประสิทธิภาพของขั้นตอนวิธี ก็จะเดาได้ทันทีว่าโจทย์ข้อนี้ต้องเลือกใช้ขั้นตอนวิธีที่มีความซับซ้อนไม่เกิน $O(n^6)$ และเทคนิคที่ไม่นึกถึงไม่ได้สำหรับความซับซ้อนตระกูลนี้ ก็คงหนีไม่พ้นการใช้กำหนดการพลวัตนั่นเอง
ถึงกระนั้น เราจะมองโจทย์ดังกล่าวให้สามารถถูกแก้โดยกำหนดการพลวัตได้อย่างไร เพราะแนวคิดพื้นฐานของการใช้เทคนิคนี้ คือ เราจะแบ่งปัญหาตั้งต้นออกเป็นปัญหาชิ้นเล็กๆ ที่เหลื่อมกันเป็นลำดับขั้น แล้วเริ่มแก้ปัญหาชิ้นเล็กที่สุด (ที่ไม่เหลื่อมกับปัญหาชิ้นอื่นใด) ไล่ขึ้นมาเรื่อยๆ โดยเมื่อต้องแก้ปัญหาชิ้นใหญ่ที่เหลื่อมกับปัญหาชิ้นเล็กที่เคยแก้ไว้แล้ว เราก็จะประหยัดเวลาโดยการนำผลลัพธ์ของการแก้ปัญหาเล็กมาช่วยได้เลยโดยไม่ต้องเริ่มแก้ปัญหาทั้งหมดตั้งแต่ต้น
แต่โจทย์ข้อนี้มีกฎว่าหยดน้ำฝนเมื่อตกกระทบพื้นแล้วสามารถไหลไปได้ทั้งทางซ้ายและขวา ทำให้มองเผินๆ เหมือนกับว่าเราจะไม่สามารถใช้เทคนิคกำหนดการพลวัตได้ เพราะปัญหาย่อยนั้นจะเหลื่อมกันไปหมดจนไม่มีปัญหาที่ไม่เหลื่อมกับปัญหาอื่นให้เริ่มต้นแก้
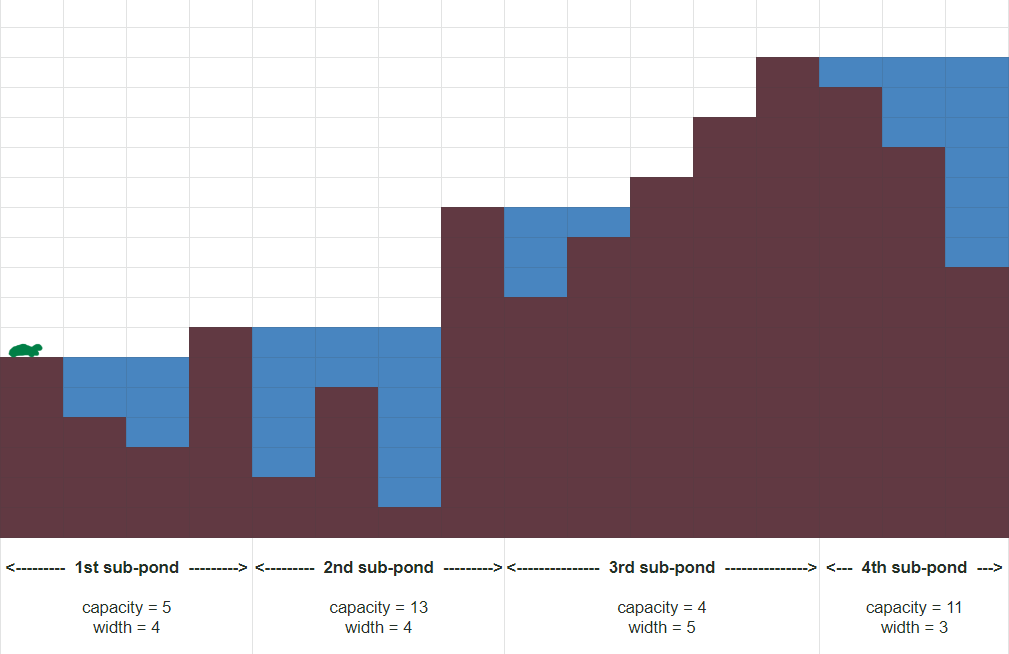
อย่างไรก็ตาม เราสามารถแปลงข้อมูลความสูงต่ำของตำแหน่งต่างๆ บนแผนที่ในโจทย์ ให้กลายเป็นบ่อน้ำย่อยๆ หลายบ่อเรียงกัน ที่แต่ละบ่อถูกนิยามผ่านความจุและความกว้าง พร้อมวางรากฐานกฎใหม่ไว้ว่าเมื่อแต่ละบ่อรองรับน้ำจนเต็มแล้ว น้ำที่ล้นออกมาจะไหลไปยังบ่อทางซ้ายเท่านั้น และถือว่าน้องเต่าจมน้ำเมื่อน้ำล้นออกจากบ่อซ้ายสุด การแปลงนี้ค่อนข้างง่ายและขอฝากไว้เป็นการบ้านสำหรับคนอ่าน 😜
ตัวอย่างการแปลงแผนที่บ่อน้ำให้กลายเป็นบ่อน้ำย่อยๆ ที่เมื่อน้ำล้นจะล้นไปยังบ่อทางซ้ายเท่านั้น
ดังนั้น จากบ่อน้ำตั้งต้นที่มีความกว้าง $n$ หน่วย เราจะแปลงมันเป็นบ่อน้ำย่อยๆ จำนวน $m \le n$ บ่อ โดยบ่อที่ $i$ สามารถจุน้ำฝนได้ $c_i$ หยด และมีความกว้าง $w_i$ หน่วย
สังเกตว่า บ่อซ้ายสุด (เรียกว่าบ่อที่ $1$) อาจจะมีความจุเท่ากับศูนย์ก็ได้ หากทุกตำแหน่งทางขวาในบ่อย่อยนั้นมีความสูงมากกว่าปากบ่อด้านซ้าย และที่บ่อขวาสุด (ซึ่งก็คือบ่อที่ $m$) อาจจะไม่มีขอบบ่อด้านขวาก็ได้ โดยถือว่าขอบขวาของบ่อนี้สูงอย่างน้อยเท่ากับขอบซ้ายได้เลย
กำหนดการพลวัตตรงไปตรงมา
ใจความของการใช้กำหนดการพลวัตมาช่วยแก้ปัญหาข้อนี้ เราจะสนใจว่าเมื่อน้ำฝนหยดมาแล้ว $d$ หยด จะมีกี่วิธีที่แตกต่างกันที่น้ำฝนล้นออกมาท่วมน้องเต่า ซึ่งเมื่อนำไปหารกับวิธีที่น้ำฝนสามารถตกได้ทั้งหมด ก็จะได้ค่า $P(X=d)$ ออกมานั่นเอง
ให้ $S(i,d)$ เป็นจำนวนวิธีที่น้ำฝนจะเริ่มท่วมน้องเต่าเมื่อฝนตกมา $d$ หยดพอดี โดยพิจารณาเฉพาะบ่อน้ำตั้งแต่บ่อซ้ายสุดจนถึงบ่อที่ $i$ สังเกตว่าเราจะมีน้ำฝนที่อิสระในการเลือกตก $d-1$ หยด ส่วนหยดสุดท้ายเป็นหยดที่บังคับตกลงมาแล้วทำให้น้ำล้นจนท่วมน้องเต่า
ดังนั้นจะเห็นว่า หากต้องการเพิ่มบ่อน้ำทางขวาเข้ามา โดยใช้ความรู้ของ $S(i, d)$ ที่คำนวณไว้แล้วก่อนหน้ามาช่วย เราจะเพิ่มน้ำฝนอิสระชุดใหม่เข้าไปสลับตำแหน่งกับน้ำฝนอิสระชุดเดิมที่มีอยู่แล้วโดยที่ไม่ทำให้น้องเต่าจมน้ำและไม่ทำให้ทุกบ่อเต็ม แล้วอาศัยน้ำฝนที่ไม่อิสระหยุดสุดท้ายของชุดเก่าเป็นหยดที่ทำให้น้องเต่าจมน้ำ อย่างไรก็ตาม หากน้ำฝนอิสระทั้งสองชุดตกมาจนเต็มแลทุกบ่อแล้วยังไม่ทำให้น้องเต่าจมน้ำ ก็จะเข้ากรณีพิเศษที่ฝนหยดสุดท้ายจะตกตรงไหนก็ได้ ซึ่งจะเปลี่ยนไปคูณกับวิธีที่น้ำฝนตกมา $d$ หยดแล้วเต็มบ่อพอดีโดยที่ไม่เคยท่วมน้องเต่าแทน
ให้ $H(i,d)$ เป็นจำนวนวิธีที่น้ำฝนจะไม่ท่วมน้องเต่าเมื่อฝนตกมาแล้ว $d$ หยด โดยพิจารณาเฉพาะบ่อน้ำตั้งแต่บ่อซ้ายสุดจนถึงบ่อที่ $i$ เราจะเขียนสมการสำหรับหา $S$ และ $H$ ได้ดังนี้
\[\begin{align} S(i, d+1) &= \begin{cases} \displaystyle \left( \sum_{k = 1}^i w_k \right) \cdot H(i, d) & \displaystyle \text{if } d = \sum_{k=1}^i c_k \\ \displaystyle \sum_{\substack{a, b \in \mathbb{N}_0 \\ a+b = d}} \binom{d}{b} \cdot w_i^b \cdot S(i, a+1) & \displaystyle \text{if } d \lt \sum_{k=1}^i c_k \\ 0 & \text{otherwise} \end{cases} \\ \\ H(i, d) &= \begin{cases} 1 & \text{if } i = 0 \text{ and } d = 0 \\ \displaystyle \sum_{\substack{a, b \in \mathbb{N}_0 \\ a+b = d}} \binom{d}{b} \cdot w_i^b \cdot H(i, a) & \displaystyle \text{if } d \le \sum_{k=1}^i c_k \\ 0 & \text{otherwise} \end{cases} \end{align}\]และทำให้ได้ว่าคำตอบคือ
\[E(X) = \sum_{d \in \mathbb{N}} d \cdot \frac{S(m, d)}{n^d}\]ใช้เทคนิคความน่าจะเป็นเข้าช่วย
วิธีคำนวณข้างต้นแม้จะตรงไปตรงมาแต่ก็มีความซับซ้อนสูง แถมยังต้องใช้กำหนดการพลวัตเก็บตัวแปรถึงสองตัว อย่างไรก็ตามเราอาจแปลงโจทย์ให้คำนวณได้ง่ายยิ่งขึ้น โดยสังเกตว่าค่าคาดหวังมีสมบัติดังนี้
\[\begin{align} E(X) &= \sum_{d \in \mathbb{N}} d \cdot P(X=d) \\ &= 1 \cdot P(X=1) + 2 \cdot P(X=2) + 3 \cdot P(X=3) + \cdots \\ &= \begin{pmatrix} P(X=1) &+& P(X=2) &+& P(X=3) &+& \cdots \\ &+& P(X=2) &+& P(X=3) &+& \cdots \\ & & &+& P(X=3) &+& \cdots \\ & & & & &+& \ddots \end{pmatrix} \\ &= P(X \ge 1) + P(X \ge 2) + P(X \ge 3) + \cdots \\ &= \sum_{d \in \mathbb{N}} P(X \ge d) \end{align}\]ดังนั้นเราจะมาแปลความหมายของ $P(X \ge d)$ กัน เพราะว่า $X$ เป็นตัวแปรสุ่มแทนน้ำฝนหยดที่ทำให้น้องเต่าจมน้ำ นั่นก็แปลว่า $X \ge d$ จะหมายถึงเหตการณ์ที่น้ำฝนหยดใดก็ได้ตั้งแต่หยดที่ $d$ ขึ้นไป (จนถึง $\infty$) ที่ทำให้น้องเต่าจมน้ำ หรืออีกนัยหนึ่งก็คือ น้ำฝนตั้งแต่หยดที่ $0$ ถึง $d-1$ นั้นไม่ทำให้น้องเต่าจมน้ำนั่นเอง
ให้ $Y$ เป็นตัวแปรสุ่มแทนจำนวนน้ำฝนที่หยดลงไปแล้วยังไม่ทำให้น้องเต่าจมน้ำ เราจะเห็นทันทีว่า
\[P(X \ge d) = P(Y = d-1)\]เนื่องจาก $P(Y=d)$ สามารถคำนวณได้จาก ${H(m,d)}$ นี่ทำให้เราสามารถลดการคำนวณเหลือเพียงเท่านี้
\[\begin{align} E(X) &= \sum_{d \in \mathbb{N}_0} P(Y=d) \\ &= \sum_{d \in \mathbb{N}_0} \frac{H(m,d)}{n^d} \end{align}\]เพื่อหาคำตอบได้เช่นกันโดยไม่ต้องง้อการคำนวณตัวแปร $S$ ที่ยุ่งยากอีกต่อไป
โค้ด
from fractions import Fraction
from itertools import count
def composition(n):
for i in range(n+1):
yield i, n-i
def choose(n, r, mem={}):
if (n,r) not in mem:
if r == 0 or r == n:
mem[n,r] = 1
else:
mem[n,r] = choose(n-1, r) + choose(n-1, r-1)
return mem[n,r]
def find_intervals(depths):
k = 0
intervals = []
for i, j in zip(count(0), count(1)):
if j == len(depths):
intervals += [(k, j)]
break
elif depths[i] < depths[k] and depths[i] < depths[j]:
intervals += [(k, i)]
k = i
return intervals
def transform(depths):
intervals = find_intervals(depths)
capacities = [0 for _ in intervals]
for i, (a, b) in enumerate(intervals):
for c in range(a, b):
if depths[c] < depths[a]:
break
capacities[i] += depths[c] - depths[a]
sizes = [b-a for a, b in intervals]
sizes[0] += 1
sizes[-1] -= 1
return capacities, sizes
def calculate_expectation(depths):
capacities, widths = transform(depths)
n = len(depths)
m = len(capacities)
limit = sum(capacities) + 1
hold = [[0 for _ in range(limit)] for _ in range(m+1)]
hold[0][0] = 1
acc_capacity = 0
for i, (capacity, width) in enumerate(zip(capacities, widths)):
acc_capacity += capacity
for d in range(acc_capacity+1):
for a, b in composition(d):
hold[i+1][d] += choose(d, b) * width**b * hold[i][a]
return sum(Fraction(hold[m][d], n**d) for d in range(limit))
def formatting(frac, prime=1_000_000_007):
return frac.numerator * pow(frac.denominator, prime-2, prime) % prime
for t in range(int(input())):
_ = input()
depths = [int(x) for x in input().split()]
answer = calculate_expectation(depths)
print(f'Case #{t+1}: {formatting(answer)}')

author, illustrator

Nonthaphat Wongwattanakij
coauthor, coder