18 สิงหาคมอาจไม่ใช่วันที่สลักสำคัญสำหรับใครหลายคนเท่าไหร่ แต่เมื่อ 153 ปีก่อน ณ ตำแหน่งหนึ่งในอาณาจักรเล็กๆ ทางเอเชียตะวันออกเฉียงใต้ที่ไม่เคยตกเป็นเมืองขึ้นต่อชาติใด ได้ปรากฎเงามืดของดวงจันทร์พาดผ่านลงมายังพื้นโลก ซึ่งถูกทำนายไว้ได้อย่างแม่นยำโดยเจ้าผู้ครองนครในช่วงเวลานั้น จนเรียกได้ว่าเป็นหมุดหมายสำคัญที่วางรากฐานให้กับวิทยาศาสตร์ในประเทศดังกล่าวกันเลยทีเดียว … ว่าแต่ว่าการคำนวณเงาจันทร์เนี่ย เค้าทำได้กันยังไงน้อ?

วงโคจรเอ๋ยจงซับซ้อนขึ้นอีก

มนุษย์โลกเรานั้นตั้งข้อสังเกตมาเนิ่นนานแล้วว่าโลกมีสัณฐานเป็นทรงกลม และเช่นเดียวกับกับเทหวัตถุบนท้องฟ้าทั้งหลายอย่างดวงอาทิตย์และดวงจันทร์ด้วย แต่ในด้านเส้นทางโคจรนั้นเราใช้เวลาไม่น้อยเลยกว่าจะเลิกสำคัญตนผิดคิดว่าโลกเป็นจุดศูนย์กลางของจักรวาล ซึ่งเริ่มจากสังเกตข้อมูลทางเดินของดาวเคราะห์ที่มีรูปแบบการโคจรแตกต่างออกไปจากดาวฤกษ์พื้นหลัง และยอมรับว่าหากให้ดาวเคราะห์ต่างๆ โคจรรอบดวงอาทิตย์เป็นวงกลมแล้วจะทำให้คำอธิบายง่ายลงกว่าเดิมมาก

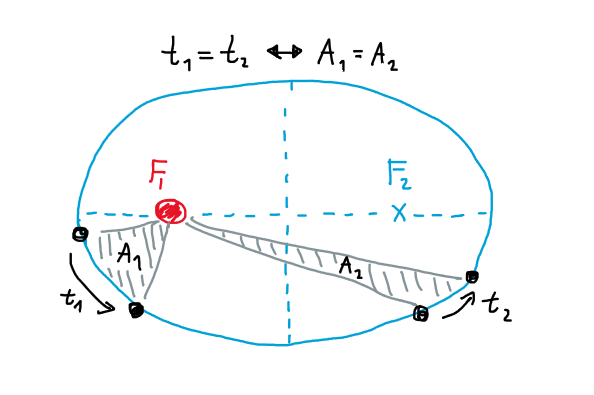
แต่นั่นก็เป็นเพียงคำอธิบายที่ลดทอนให้เรียบง่ายเพื่อบรรจุลงในบทเรียนดาราศาสตร์พื้นฐานในปัจจุบัน เพราะหากดูรายละเอียดให้ลึกลงไปแล้ว การให้วงโคจรดาวเคราะห์เป็นวงกลมและเคลื่อนที่ด้วยความเร็วคงที่ ก็ไม่ได้ช่วยทำนายวงโคจรได้อย่างแม่นยำเสียทีเดียว โลกเรายังต้องรอการเก็บบันทึกข้อมูลเส้นทางดาวอันแม่นยำนับหลายทศวรรษจาก Tycho Brahe และการตีความข้อมูลจากลูกศิษย์ Johannes Kelper จนทำให้เราได้โมเดลที่แม่นยำว่าดาวเคราะห์โคจรเป็นวงรีรอบดวงอาทิตย์ที่อยู่ ณ จุดโฟกัสจุดหนึ่ง โดยเส้นตรงเชื่อมดาวเคราะห์ถึงดวงอาทิตย์จะกวาดพื้นที่ ณ ช่วงใดๆ ได้เท่ากันเมื่อเวลาผ่านไปเท่ากัน ซึ่งแม้เราจะไม่ค่อยเห็นผลชัดเจนสำหรับดาวเคราะห์หลักๆ ที่มีวงโคจรเกือบเป็นวงกลม แต่โมเดลนี้ก็สอดคล้องเป็นอย่างดีกับบรรดาดาวหางที่มีวงโคจรเป็นวงรีอย่างชัดเจน ที่จะเดินทางเร็วขึ้นเมื่อเข้าใกล้ดวงอาทิตย์นั่นเอง

กฎการเคลื่อนที่ดาวเคราะห์ของ Kepler

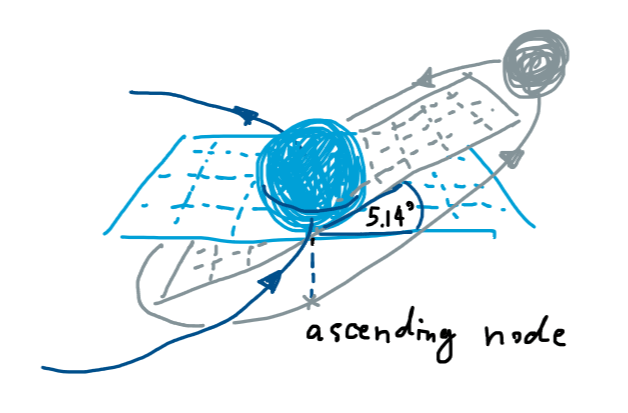
และนอกจากนี้เรายังสังเกตว่าได้อีกว่า วงโคจรของดาวเคราะห์ต่างๆ รอบดวงอาทิตย์ก็ไม่ได้อยู่ในระนาบเดียวกันพอดีเป๊ะอีก แต่จะมีความเอียงของวงโคจรมากบ้างน้อยบ้างตามลักษณะเฉพาะของดาวแต่ละดวง ซึ่งเมื่อนำแนวคิดนี้มาใช้กับข้อมูลที่สังเกตได้จากดวงจันทร์ของโลก โดยให้ระนาบที่โลกโคจรรอบดวงอาทิตย์เป็น 0° จะได้ว่าระนาบสัมพัทธ์ของดวงจันทร์ที่โคจรรอบโลกอยู่ที่ 5.14° ซึ่งดูเผินๆ แม้จะเป็นมุมนิดเดียว แต่อย่าลืมว่าดวงจันทร์นั้นอยู่ห่างจากโลกเป็นระยะทางเฉลี่ยประมาณ 385,00 กิโลเมตร ดังนั้นเมื่อดวงจันทร์อยู่ ณ จุดสูงสุด (หรือต่ำสุด) บนระนาบวงโคจรรอบโลก มันจะอยู่ห่างจากระนาบที่โลกโคจรรอบดวงอาทิตย์ได้สูงถึง 33,000 กิโลเมตรเลยทีเดียว นี่เป็นระยะทางที่สูงกว่าการนำโลกอีกสองใบมาวางเทินบนโลกใบเดิมเสียอีก!

ระนาบวงโคจรของดวงจันทร์ที่เอียง 5.14°

ดังนั้นการจะเกิดสุริยุปราคาได้ เพียงแค่ดวงจันทร์โคจรมาอยู่ระหว่างโลกและดวงอาทิตย์ยังไม่พอ แต่ดวงจันทร์ยังต้องอยู่ในบริเวณที่ระนาบทั้งสองตัดกันอีกด้วย เราเรียกจุดบนวงโคจรที่ระนาบทั้งสองตัดกันว่าโหนด ซึ่งจะมีสองโหนดได้แก่โหนดขึ้นและโหนดลงนั่นเอง และแม้ว่าการที่ดวงจันทร์โคจรรอบโลกหนึ่งรอบจะต้องผ่านโหนดทั้งสองอย่างละหนึ่งครั้ง แต่เพราะโลกก็โคจรรอบดวงอาทิตย์ด้วยเช่นกัน จึงทำให้จังหวะที่โหนดหนึ่งๆ จะอยู่ตรงกลางระหว่างโลกและดวงอาทิตย์พอดีมีเพียงแค่สองครั้งในหนึ่งปี นี่จึงเป็นเหตุผลว่าทำไมโลกเราจึงไม่มีเหตุการณ์สุริยุปราคาอันแสนตื่นเต้นให้ได้ติดตามรับชมทุกเดือน แต่ในหนึ่งปีจะมีเหตุการณ์นี้เกิดขึ้นได้เพียงสองครั้งเท่านั้นนั่นเอง

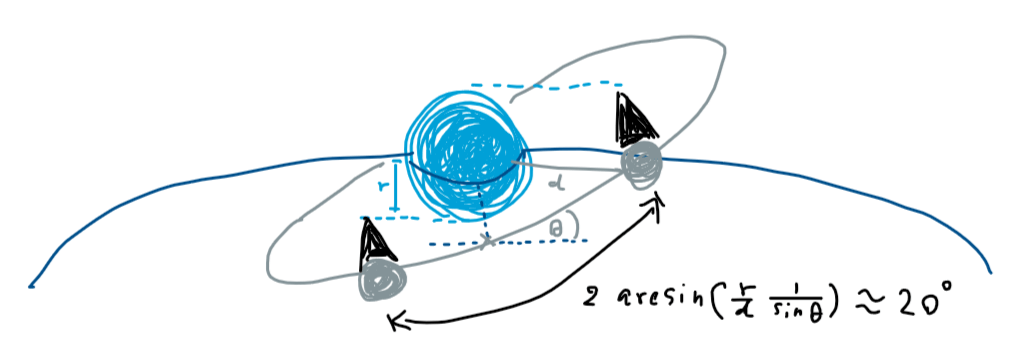
แต่การเกิดสุริยุปราคานี้ดวงจันทร์ไม่จำเป็นต้องอยู่บนโหนดพอดีก็ได้ เพียงแค่อยู่ใกล้เคียงก็พอ เราสามารถประมาณปัญหานี้เป็นโจทย์ตรีโกณมิติอย่างหยาบๆ ได้ กล่าวคือดวงจันทร์ไม่ควรอยู่ห่างจากระนาบที่โลกโคจรรอบดวงอาทิตย์เป็นระยะทางสูง/ต่ำเกินรัศมีของโลก นี่ทำให้ได้ช่วงบนวงโคจรขนาดประมาณ 20° รอบโหนดที่ยังพอมีหวังให้เกิดสุริยุปราคาได้นั่นเอง

ระยะใกล้เคียงกับโหนดที่ใกล้มากพอที่เงาของดวงจันทร์จะยังตกกระทบผิวโลก

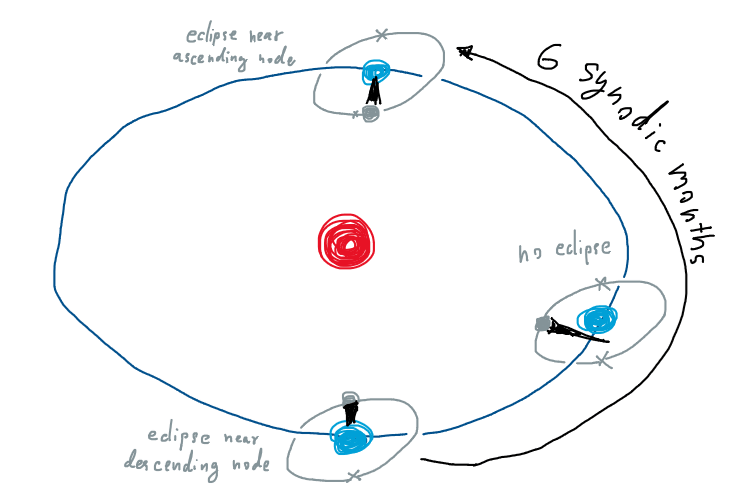
และอันที่จริงเราก็ไม่ได้เห็นสุริยุปราคาปีละสองครั้งพอดีเป๊ะซะทีเดียว เพราะถ้าดูรายละเอียดคาบการโคจรแล้ว จะพบว่าโลกใช้เวลาประมาณ 365.25 วันในการโคจรรอบดวงอาทิตย์หนึ่งรอบ ส่วนดวงจันทร์ใช้เวลาประมาณ 29.53 วันในการโคจรรอบโลกครบหนึ่งรอบเมื่อเทียบดวงอาทิตย์เป็นฉากหลัง (คาบซินอดิก) สังเกตว่า 6 รอบซินอดิกมีค่า 177.18 วัน ซึ่งใกล้เคียงกับระยะเวลาที่โลกใช้เพื่อโคจรรอบดวงอาทิตย์ครึ่งรอบอยู่มาก นั่นหมายความว่าหากมีเหตุการณ์สุริยุปราคาเกิดขึ้นเมื่อดวงจันทร์อยู่ ณ ตำแหน่งโหนดพอดี เมื่อผ่านไปอีก 177 วันกับอีกสี่ชั่วโมงครึ่งนิดๆ ก็จะเกิดสุริยุปราคาได้อีกครั้งเพราะดวงจันทร์ขยับกลับเข้ามาใกล้กับโหนดในด้านตรงกันข้ามนั่นเอง

การวนไปจนเจอโหนดฝั่งตรงข้ามและเกิดสุริยุปราคาอีกครั้ง

แต่ว่าตำแหน่งของโหนดทั้งสองก็ไม่ได้อยู่นิ่งๆ ค้างฟ้าอยู่เรื่อยไป เพราะระนาบวงโคจรของดวงจันทร์นั้นก็หมุนรอบโลกไปเรื่อยๆ ด้วยเช่นกัน โดยมันหมุนไปในทิศทางตรงกันข้ามกับที่ดวงจันทร์โคจรรอบโลก ซึ่งจะหมุนกลับมาครบรอบเดิมทุกๆ 18.6 ปีโลก เราวัดระยะเวลาที่ดวงจันทร์โคจรครบหนึ่งรอบแล้วกลับมายังโหนดเดิม (คาบดราโคนิค) ได้ 27.21 วัน นี่หมายความว่าในเวลา 177.18 วัน ดวงจันทร์จะอยู่ห่างจากโหนดด้านตรงข้ามเพียง 4.0° เท่านั้น แต่ในหนึ่งรอบซินอดิก 29.53 วันนั้นดวงจันทร์โคจรได้ระยะมุมเป็น 29.1° นั่นหมายความว่าโดยประมาณแล้วเมื่อครบ 7 รอบการเกิดสุริยุปราคาที่ทิ้งช่วงกัน 6 เดือน จะมีสุริยุปราคาที่ทิ้งช่วงเพียง 5 เดือนมาคั่นอยู่หนึ่งครั้ง หรือบางครั้งก็เกิดเป็นสุริยุปราคาติดกันสองเดือน เพราะดวงจันทร์โคจรคร่อมระหว่างโหนดในระยะที่เอื้อให้เกิดสุริยุปราคาได้ทั้งคู่พอดี (ตัวอย่างเช่นในปี 2011 เกิดสุริยุปราคาวันที่ 1 มิถุนายน และ 1 กรกฎาคม)

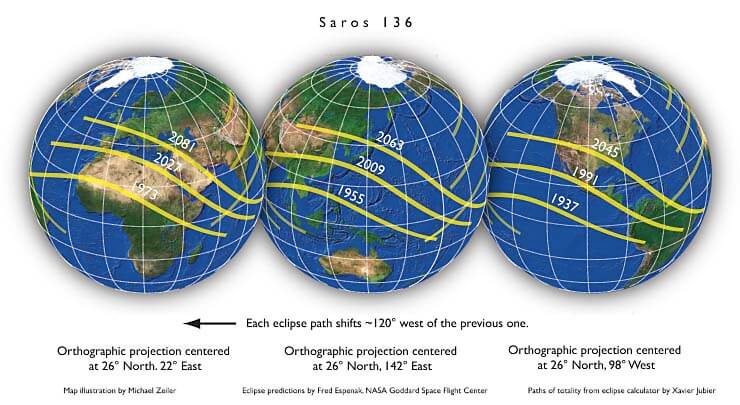
และถ้าเราขยายข้อสังเกตนี้ออกไปเป็นช่วงที่ยาวและละเอียดขึ้น เราก็จะได้คาบแซรอส ซึ่งกินเวลา 18 ปี 10 วันกับอีก 8 ชั่วโมง เพราะว่าคาบซินอดิก (29.53 วัน) จำนวน 223 รอบเท่ากับ 6,585.2 วัน และคาบดราโคนิก (27.21 วัน) จำนวน 242 รอบเท่ากับ 6584.8 วัน ซึ่งนับว่าใกล้เคียงกันมาก ทำให้เมื่อครบคาบแซรอสแล้วตำแหน่งของดวงอาทิตย์โลกและดวงจันทร์จะคล้ายกับถูกรีเซ็ตให้กลับมาอยู่ที่เดิม (ไม่เป๊ะเสียทีเดียวแต่ก็ใกล้เคียงมาก) ทำให้การเกิดสุริยุปราคาครั้งถัดไปแทบจะเรียกได้ว่าซ้ำรอยกับครั้งก่อนหน้าในคาบแซรอสที่แล้ว จะยกเว้นก็เพียงแต่เรื่องเวลา 8 ชั่วโมงที่เกินออกมา ที่บอกว่าสุริยุปราคานั้นเลื่อนไปเกิด ณ ตำแหน่งหนึ่งในสามซีกโลกถัดไปเท่านั้น

พยากรณ์การเกิดสุริยุปราคาในคาบแซรอสหมายเลข 136 ภาพจาก NASA

นั่นหมายความว่า ถ้าเราเก็บข้อมูลสุริยุปราคามาเพียงประมาณสองทศวรรษ เราก็จะพยากรณ์วันเวลาที่จะเกิดสุริยุปราคาในอนาคตถัดๆ ไปได้อย่างไม่น่าเกลียดแล้ว (แต่ความเป็นจริงเราอาจต้องเก็บข้อมูลเป็นศตวรรษ กว่าจะสร้างโมเดลที่ทำนายได้แม่นยำ กว่าจะชักนำสังคมให้หันมาเข้าใจการคำนวณต่างๆ)

ทางของเงา

คำถามต่อมาคือ แล้วเราจะพยากรณ์ตำแหน่งที่เงาของดวงจันทร์จะพาดผ่านบนผิวโลกได้อย่างไร? ก่อนอื่นเราควรมารู้จักเงาที่เกิดจากดวงจันทร์บังดวงอาทิตย์เสียก่อน ซึ่งแบ่งได้เป็น 3 แบบดังนี้

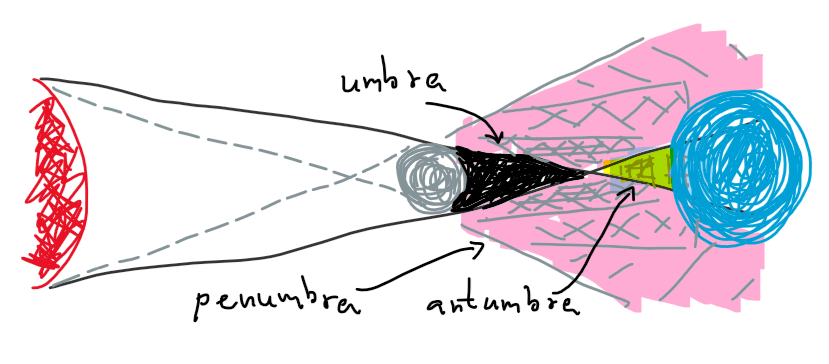
1. เงา umbra เป็นเงามืดสนิทเพราะดวงจันทร์บังดวงอาทิตย์มิด หากอยู่บริเวณนี้เราจะสังเกตเห็นสุริยุปราคาเต็มดวงได้
2. เงา penumbra เป็นเงาที่มีลักษณ์เป็นดวงจันทร์กัดดวงอาทิตย์แหว่งไป ดังนั้นเราจะเห็นสุริยุปราคาบางส่วน (ดวงอาทิตย์เป็นเสี้ยว)
3. เงา antumbra เป็นเงาที่ดวงจันทร์พยายามบังดวงอาทิตย์ด้วยตัวเองทั้งหมด แต่บังไม่มิดเพราะขนาดปรากฏบนท้องฟ้าของดวงจันทร์เล็กกว่าดวงอาทิตย์นั่นเอง นี่ทำให้เราได้สุริยุปราคาวงแหวน

บริเวณเงาทั้งสามแบบที่เกิดขึ้นได้ ระบายสีแยกกันชัดเจนเพื่อป้องกันความสับสนว่าเป็นความเข้มเงา

การจะบอกได้ว่าสุริยุปราคาครั้งใดให้เงาแบบไหน ทำได้ผ่านการคำนวณขนาดปรากฏของทั้งดวงอาทิตย์และดวงจันทร์บนท้องฟ้า ณ เวลาที่จะเกิดสุริยุปราคา ซึ่งจากที่เราทราบแล้วว่าวงโคจรของเทหวัตถุทั้งหลายบนท้องฟ้าล้วนเป็นวงรี จึงทำให้มีช่วงที่เทหวัตถุเหล่านั้นเข้าใกล้หรือห่างไกลจากเรามากกว่าค่าเฉลี่ย แม้การสังเกตด้วยตาเปล่าจะไม่มีทางแยกความแตกต่างได้ (ขนาดของดวงอาทิตย์นั้นถือว่าค่อนข้างคงที่ที่ประมาณ 0.53° ส่วนดวงจันทร์นั้นผันแปรอยู่ในช่วงตั้งแต่ 0.49° ถึง 0.57° เลยทีเดียว) แต่มันก็ส่งผลอย่างมากต่อชนิดของสุริยุปราคาที่เราจะสังเกตได้ อันที่จริงแล้วในคาบแซรอสนั้นเราก็ได้พิจารณาถึงคาบที่ดวงจันทร์เริ่มจากจุดที่อยู่ใกล้โลกที่สุดแล้วโคจรรอบโลกหนึ่งรอบจนกลับมาอยู่ที่จุดใกล้โลกที่สุดอีกครั้ง (คาบวิปริต) ที่มีค่า 27.55 วันอีกด้วย จึงทำให้สุริยุปราคาแต่ละครั้งมีลักษณ์คล้ายกันมาก เพราะดวงจันทร์กลับไปอยู่ในตำแหน่งที่ใกล้/ไกลจากโลกเช่นเดียวกับครั้งก่อนๆ นั่นเอง และเมื่อทราบถึงขนาดเชิงมุมของดวงอาทิตย์และดวงจันทร์ในสุริยุปราคาครั้งนั้นๆ แล้ว เราก็ควรคำนวณรัศมีของเงาแบบต่างๆ ผ่านตรีโกณมิติได้อย่างไม่ยากเย็นอะไร

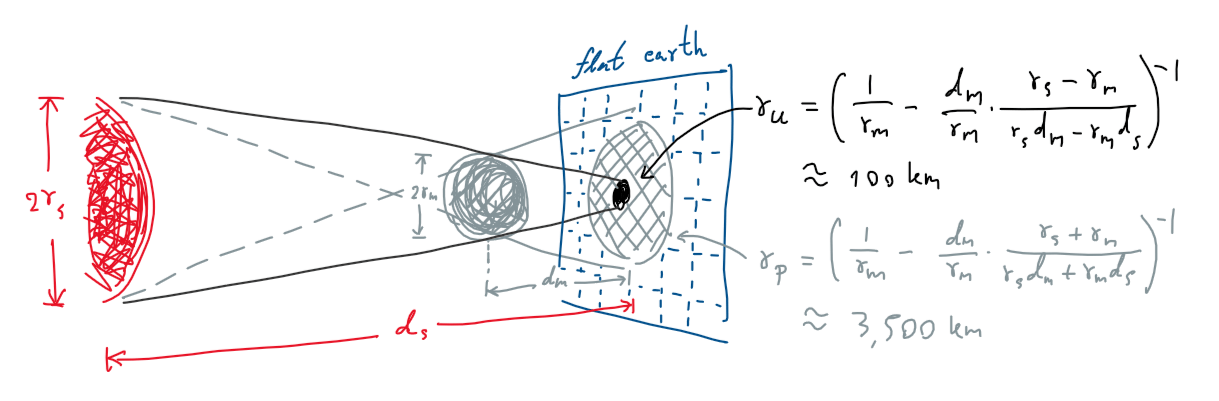
รัศมีของเงาสองประเภทที่ถูกฉายบนพื้นโลก

กลับมาที่การหาบริเวณที่เงาจะพาดผ่าน สังเกตว่ารัศมีของโลกนั้นมีค่าเพียงเล็กน้อยแทบจะเทียบไม่ได้เลยกับระยะห่างจากโลกถึงดวงจันทร์ ดังนั้นเพื่อลดทอนความยุ่งยากในโมเดลพื้นฐาน เราอาจมองว่าโลกแบนและตั้งฉากกับดวงอาทิตย์และดวงจันทร์เลยก็ได้ ซึ่งเมื่อเราจับดวงจันทร์ให้โคจรผ่านหน้าโลกเป็นเพียงระยะเวลาสั้นๆ แล้ว เราก็จะเห็นเส้นทางเงาที่วิ่งจากขอบหนึ่งของโลกไปยังอีกขอบอย่างเรียบง่ายเป็นเส้นตรงได้อย่างไม่ยากเย็นอะไร

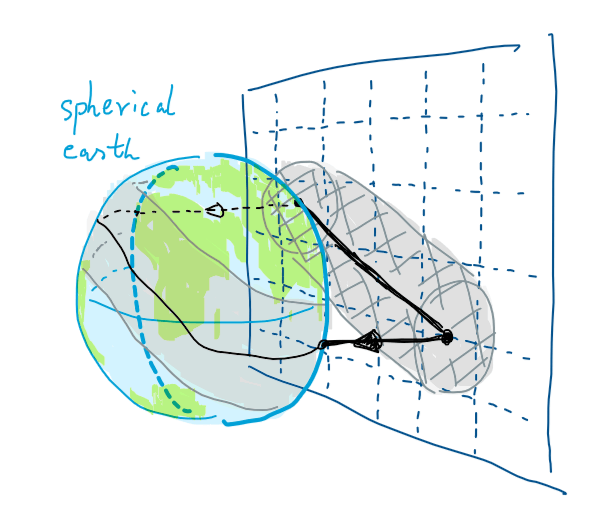
ซึ่งนั่นก็เป็นหัวใจของโมเดลเงาสุริยุปราคาที่ Friedrich Bessel พัฒนาขึ้นมาในปี 1824 และยังถูกใช้จนถึงปัจจุบัน แต่การคำนวณจริงไม่ได้ง่ายดายและจบเพียงเท่านั้นเพราะ 1) โลกไม่ได้แบน 2) แกนหมุนโลกเอียง 23.44° และ 3) โลกหมุนรอบตัวเองตลอดเวลา ดังนั้นเมื่อเราได้เส้นทางของเงาบนระนาบมาแล้ว เราจึงต้องฉายภาพเงากลับไปยังผิวโลกที่เป็นทรงกลมด้วย จึงทำให้ได้เส้นทางเงาที่ดูคดโค้งไม่สามารถคาดเดาได้โดยง่ายเหมือนอย่างตอนฉายลงระนาบนั่นเอง

การฉายภาพเงาจากระนาบสมมติฐานโลกแบนกลับไปยังลูกโลกทรงกลมเหมือนจริง

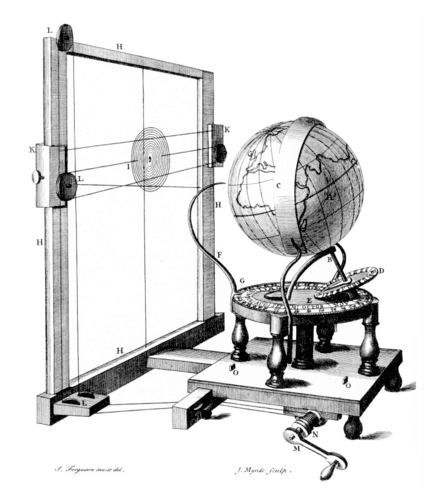
แล้วคนทำแผนที่เค้าต้องมานั่งคำนวณอะไรยุ่งยากเช่นนี้ทุกครั้งหรือ? อย่างที่เราได้รู้จักกับคาบแซรอสไปแล้ว นั่นหมายความข้อมูลการเกิดสุริยุปราคาเมื่อ 18 ปีก่อน (ที่ไม่จำเป็นต้องมาจากการคำนวณแต่เป็นการสังเกตก็ได้) จะช่วยนำทางให้การคำนวณเส้นทางเงาครั้งใหม่ง่ายขึ้นมาก นอกจากนี้ยังมีการประดิษฐ์เครื่องฉายสุริยุปราคามาตั้งแต่ปี 1756 หรือมีการจัดพิมพ์รายงานเส้นทางเงาออกมาเป็นรูปเล่มที่ไม่เพียงเฉพาะสำหรับนักเดินเรือ แต่ยังจับตลาดบุคคลทั่วไปตั้งแต่ 1737 แล้วด้วย

เครื่องฉายสุริยุปราคา eclipseareon ของ James Ferguson ในปี 1756

คำนวณรายละเอียด ณ จุดสังเกตการณ์

แม้การคำนวณที่ผ่านมาจะทำให้ได้เส้นทางที่น่าสนใจเพื่อลงหลักปักฐานสังเกตการณ์ แต่การคำนวณเหล่านั้นก็ยังเป็นแค่การคำนวณหยาบๆ เพื่อให้เห็นภาพรวมของสุริยุปราคาครั้งหนึ่งเท่านั้น ซึ่ง ณ จุดสังเกตการณ์หนึ่งๆ แล้วเรายังสามารถคำนวณเวลาต่างๆ ที่ดวงจันทร์จะเข้าบังดวงอาทิตย์ได้อีก โดยสุริยุปราคาแบบเต็มดวงอาจประกอบด้วย 4 เหตุการณ์สำคัญที่น่าสนใจคือ 1) ดวงจันทร์เริ่มสัมผัสดวงอาทิตย์ 2) ดวงจันทร์บังดวงอาทิตย์ครบ 3) ดวงจันทร์เริ่มคายดวงอาทิตย์ 4) ดวงจันทร์ปล่อยดวงอาทิตย์จนหมด

จังหวะต่างๆ ที่สำคัญในการสังเกตสุริยุปราคา ภาพจาก WikiPedia

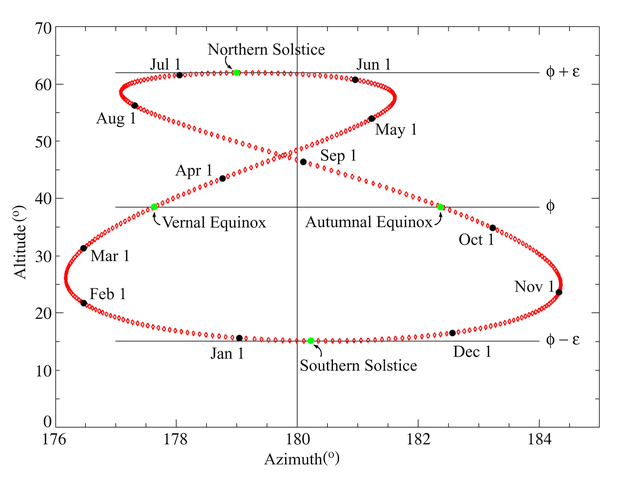
ปัญหาที่เหลือก็เป็นเพียงการหาตำแหน่งของดวงอาทิตย์และดวงจันทร์บนท้องฟ้าในช่วงเวลาต่างๆ สำหรับดวงอาทิตย์แล้วเราสามารถคำนวณตำแหน่งได้ไม่ยาก เพราะหากเราสังเกตดวงอาทิตย์ ณ เวลาเดิมของทุกวัน เราจะพบว่าดวงอาทิตย์ไม่ได้อยู่ในตำแหน่งเดิมบนท้องฟ้าเสียทีเดียว แต่จะมีการเคลื่อนที่เป็นรูปคล้ายสัญลักษณ์ ∞ ที่กินเวลายาวนานหนึ่งปีก่อนจะวนกลับมาที่เดิม ส่วนดวงจันทร์นั้นจะซับซ้อนกว่าเล็กน้อยตรงที่วงมีโคจรเอียง 5.14° เพิ่มขึ้นมานั่นเอง

แอนาเล็มมา ณ หอดูดาวหลวงเมืองเกรนิชตอนเที่ยงวัน

ประเทศไทยอยู่ตรงไหน?

ก่อนที่จะเข้าใจประวัติศาสตร์ตนเองอย่างถ่องแท้ได้ เราควรเข้าใจประวัติศาสตร์โลกควบคู่กันไปด้วย ซึ่งสรุปหลักใหญ่ใจความได้ตามตารางความรู้ของมนุษย์ชาติต่อสุริยุปราคาดังต่อไปนี้

ปี	ใคร	อะไร
22nd BC	ชาวจีน	เรื่องเล่าที่นักดาราศาสตร์ที่พลาดการทำนายสุริยุปราคา
8th BC	ชาวอัสซีเรีย	บันทึกสุริยุปราคามิถุนายน 763 BC ซึ่งเป็นจุดเชื่อมต่อให้เราสามารถเทียบเวลาในประวัติศาสตร์ได้
5th BC	ชาวบาบิโลน	แนวคิดคาบแซรอส
4th BC	Euclid of Alexandria	ศึกษาเรขาคณิตที่สามารถสร้างได้โดยสันตรงและวงเวียน
3rd BC	Eratosthenes of Cyrene	คำนวณขนาดของโลกด้วยตรีโกณมิติ
3rd BC	Apollonius of Perga	ศึกษาภาคตัดกรวย (วงกลม วงรี พาราโบลา ไฮเพอร์โบลา)
2nd BC	Hipparchus of Nicaea	คำนวณระยะจากโลกถึงดวงจันทร์โดยข้อมูลสุริยุปราคาและตรีโกณมิติ
1st BC	ชาวกรีก	ประดิษฐ์กลไก Antikythera ที่หนึ่งในเฟืองมีฟัน 223 ซี่
2nd CE	Claudius Ptolemy	แนวคิดโลกเป็นจุดศูนย์กลาง โดยมีดาวเคราะห์และดวงอาทิตย์โคจรรอบ
1543	Nicolaus Copernicus	แนวคิดดวงอาทิตย์เป็นจุดศูนย์กลาง ดาวเคราะห์โคจรเป็นวงกลม
1572	Tycho Brahe	เริ่มจดบันทึกข้อมูลตำแหน่งดาว ซึ่งต่อมาถูกใช้โดย Kepler
1609	Johannes Kepler	กฎการเคลื่อนที่ของดาวเคราะห์ที่มีวงโคจรเป็นวงรี
1610	Galileo Galilei	พิสูจน์ด้วยกล้องโทรทัศน์ว่าดวงอาทิตย์เป็นจุดศูนย์กลาง
1614	John Napier	ศึกษาเรขาคณิตทรงกลมด้วยฟังก์ชันลอการิทึมของตรีโกณมิติ
1675	John Flamsteed	เริ่มจดบันทึกข้อมูลตำแหน่งดาว ซึ่งต่อมาถูกใช้โดย Newton และ Halley
1687	Isaac Newton	กฎการเคลื่อนที่ของวัตถุและแรงโน้มถ่วง
1715	Edmond Halley	พยากรณ์สุริยุปราคาพฤษภาคม 1715 โดยประยุกต์ใช้ทฤษฎีของ Newton ทำนายพลาดไป 4 นาที
1731	John Hadley, Thomas Godfrey	ประดิษฐ์เครื่องวัดแดด (sextant)
1737	George Smith	ตีพิมพ์พยากรณ์สุริยุปราคาลง The Gentleman’s Magazine ซึ่งเป็นนิตยสารสำหรับผู้อ่านทั่วไป
1756	James Ferguson	ประดิษฐ์เครื่องฉายสุริยุปราคา Eclipsareon
1824	Friedrich Bessel	การคำนวณการฉายเส้นทางเงาสุริยุปราคาบนผิวโลก
1887	Theodor von Oppolzer	ตีพิมพ์ Canon der Finsternisse ที่พยากรณ์สุริยุปราคาและจันทรุปราคาตั้งแต่ 1207 BC ถึง 2161
1919	Albert Einstein	ใช้สุริยุปราคาเพื่อพิสูจน์ความโค้งงอของอวกาศอันเนื่องมาจากแรงโน้มถ่วง
1969	NASA	Apollo 11 ติดตั้งอุปกรณ์เพื่อวัดระยะทางจากดวงจันทร์ถึงโลก ข้อมูลที่ได้ทำให้พยากรณ์ว่าในอนาคตจะไม่มีสุริยุปราคาเต็มดวงอีกต่อไป

จากบทที่ผ่านๆ มาเราคงได้เห็นแล้วว่าการคำนวณสุริยุปราคานั้นมีรายละเอียดมากมายและแบ่งได้หลายระดับขั้น ก็นับว่าเป็นเรื่องน่าเศร้าทางการศึกษาที่ไม่มีการเรียนการสอนลงรายละเอียดเกี่ยวกับสุริยุปราคาที่หว้ากอในวันที่ 18 สิงหาคม 1868 เลย จนทำให้คนทั่วไปเข้าใจผิดคิดว่าเป็นการคำนวณสุริยุปราคาในทุกมิติ ตั้งแต่ประมวลผลข้อมูลนำมาสร้างเป็นโมเดลไปจนคำนวณวันเวลาตำแหน่งของการเกิดสุริยุปราคาแต่ละครั้งออกมา แต่ในความเป็นจริงแล้วเรามีเพียงหลักฐานการคำนวณเวลา ณ จุดสังเกตการณ์เท่านั้น เพราะด้านการสร้างโมเดลขึ้นมาเองด้วยความรู้ดั้งเดิมนั้น เป็นไปไม่ได้เลยเนื่องจากศาสตร์ที่เกี่ยวกับดวงดาวของไทย (เช่น โหร) ไม่เคยมีการจดบันทึกตำแหน่งดาวอย่างละเอียด หนำซ้ำการจดบันทึกตำแหน่งดาวของโหรก็ยังสื่อโดยนัยอีกว่าโลกเป็นศูนย์กลางของจักรวาล ความรู้เกี่ยวกับดาราศาสตร์ทั้งหมดของไทยนั้น “ก้าวกระโดด” ขึ้นมาจากสมัยก่อนหน้า เนื่องจากเรารับเอาหนังสือตำราการคำนวณของตะวันตกมาใช้งานเลยทันที

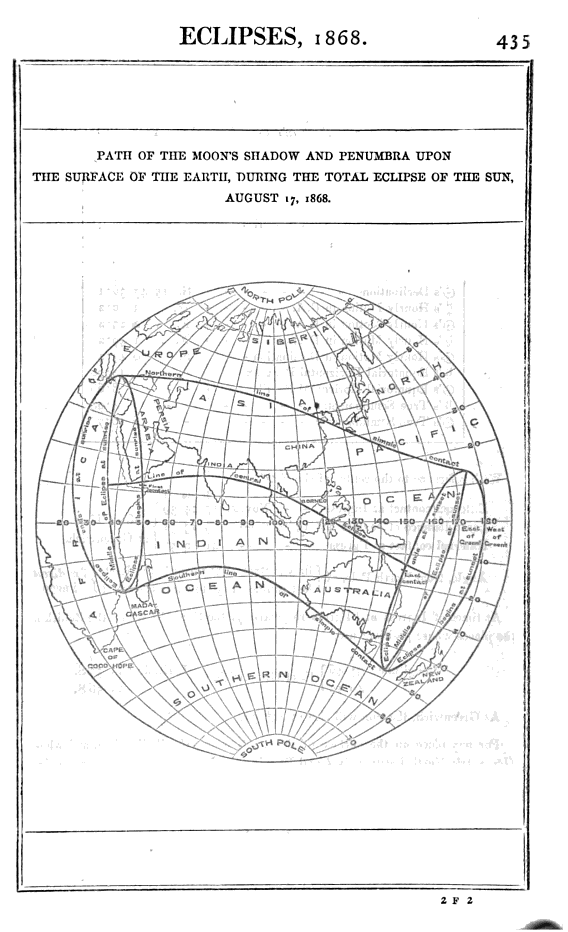
ส่วนการคำนวณเส้นทางเงาที่ยุ่งยากนั้น ก็ไม่พบหลักฐานการคำนวณ ซ้ำยังมีหลักฐานแย้งเต็มไปหมด ตั้งแต่ว่าทำไมสุริยุปราคา 1868 ถึงถูกประกาศว่าจะเกิดล่วงหน้าเพียงแค่ 2 ปีเท่านั้น ทั้งที่วิทยาการในช่วงเดียวกันสามารถคำนวณสุริยุปราคาล่วงหน้าได้นับทศวรรษ หากไม่ก็เป็นศตวรรษเรียบร้อยแล้ว อีกทั้งในเวลานั้นยังมีหนังสือ Nautical Almanac สำหรับปี 1868 ที่ตีพิมพ์ล่วงหน้าถึง 4 ปีโดยภายในมีตารางตัวเลขดวงดาวต่างๆ อย่างมากมาย พร้อมทั้งแผนที่เส้นทางการพาดผ่านของเงาอย่างชัดเจนอีกด้วย

Murray, John. “Nautical Almanac and Astronomical Ephemeris for the year 1868.”, London, (1864): 435.

นอกจากนี้การยกย่องให้ร.4 เป็นบิดาแห่งวิทยาศาสตร์ไทย ก็เพิ่งมีขึ้นตอนครบรอบรัตนโกสินทร์ 200 ปีเมื่อ 1982 ที่ผ่านมานี้เอง ทั้งยังเป็นการยกย่องแบบไม่กล่าวถึงนักวิทยาศาสตร์ที่มาก่อนหน้า หรือศึกษาลงรายละเอียดผลงานเพื่อให้นักวิทยาศาสตร์รุ่นหลังสามารถนำไปสานต่อได้เลย … ซึ่งก็ยิ่งน่าเสียดายเพราะ motto หนึ่งที่สำคัญในแวดวงวิทยาศาสตร์ก็คือ standing on the shoulders of giants นั่นเอง

อ้างอิง

• กุญแจแห่งฟากฟ้า: เรขาคณิตวิเคราะห์ จากกรีกโบราณถึงนิวตัน, ศุภวิทย์ ถาวรบุตร
• พระจอมเกล้าฯ พยากรณ์ : ความย้อนแย้งของ “ดาราศาสตร์” กับ “โหราศาสตร์” ในสังคมไทยสมัยใหม่, สิกขา สองคำชุม
• Eclipses (What Everyone Needs to Know), Frank Close
• Astronomia nova, Johannes Kepler
• Five Millennium Catalog of Solar Eclipses: –1999 to +3000, Fred Espenak and Jean Meeus
• Standford
  • The Antikythera Mechanism: A Shocking Discovery from Ancient Greece.
• Atlas Obscura
  • How Edmond Halley Kicked Off the Golden Age of Eclipse Mapping
  • Was the First Eclipse Prediction an Act of Genius, a Brilliant Mistake, or Dumb Luck?
• Max-Planck-Gesellschaft
  • When the dragon swallows the sun
• The Guardian
  • Halley’s Eclipse: a coup for Newtonian prediction and the selling of science
• Stand-up Maths
  • Solar Eclipse Maths and the Cosmic Coincidence of the Saros Cycle
  • Eclipses can be approximated the same way as π. [ONE TAKE!]
• Vox
  • Why people get so excited about a total solar eclipse
• TED-Ed
  • What creates a total solar eclipse? - Andy Cohen
• National Geographic
  • Solar Eclipse 101 | National Geographic