เจอโจทย์ความน่าจะเป็นที่เคลมว่าง่ายระดับม.ต้น แต่คนแปลโจทย์ดันแปลผิดไปนิดนึง เลยทำให้โจทย์กลายเป็นยากระดับมหา’ลัยไปซะได้ 😂 โดยเนื้อหาโจทย์เวอร์ชันต้นฉบับ (ที่พิมพ์ผิด) คือ “สับไพ่หนึ่งดอกแล้วค่อยๆ เปิดทีละใบ หากเปิดเจอใบที่มีค่าสูงที่สุดเท่าที่เคยเห็นก็จะเก็บไพ่ใบนั้นขึ้นมือ หาความน่าจะเป็นเมื่อเปิดไพ่ครบ $n=13$ ใบแล้วจะมีไพ่ขึ้นมือทั้งหมด $r$ ใบว่าเป็นเท่าไหร่” — ซึ่งจริงๆ แล้วโจทย์ที่พิมพ์ถูกควรจะถามหาแค่โอกาสที่จะเก็บไพ่หมายเลข $r$ ขึ้นมือเท่านั้น (ให้ค่า $r$ ของไพ่ $A=1$ ไล่ขึ้นไปยัง $K=13$)

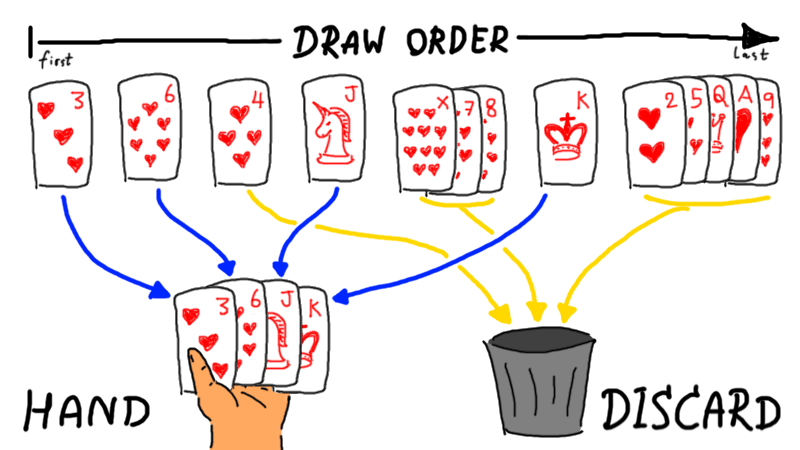
ตัวอย่างการเก็บไพ่ขึ้นมือ เมื่อเปิดเจอ $364JX78K25QA9$ ตามลำดับ จะเก็บได้ 4 ใบคือ $36JK$

งั้นก็มาลองแก้โจทย์เวอร์ชันที่พิมพ์ถูก (โจทย์ง่ายๆ) กันก่อน ว่าเมื่อเปิดไพ่ครบแล้วเราจะมีไพ่หมายเลข $r$ อยู่บนมือด้วยความน่าจะเป็นเท่าไหร่? มองผ่านๆ อาจรู้สึกว่าโจทย์นี้ก็ยังยากเพราะวิธีสับไพ่นั้นสูงถึง $13!$ แต่ถ้าลองพิจารณาจากกรณีสุดขอบเข้ามา ซึ่งในที่นี้จะเริ่มจากสนใจ $K$ จะเห็นว่ายังไงไพ่ใบนี้ก็ต้องถูกหยิบขึ้นมืออย่างแน่นอนไม่ว่าจะปรากฏตอนไหนในลำดับ เพราะว่ามันมีค่าสูงที่สุดไม่มีไพ่ใบไหนมาบังมันได้นั่นเอง

ต่อมาเราจะถอยกลับไปพิจารณาไพ่ $Q$ ซึ่งสามารถลดรูปปัญหาได้ว่า เราจะเจอไพ่ $Q$ ก่อนหรือหลัง $K$ (โดยที่ไม่ต้องสนใจไพ่อื่นๆ ที่มีค่าต่ำกว่ามันเลย) ดังนั้น $Q$ ก็จะถูกหยิบด้วยความน่าจะเป็นเพียงแค่ครึ่งหนึ่งเท่านั้น และถอยกลับไปพิจารณาไพ่ $J$ ได้ในทำนองเดียวกัน ที่เราจะสนเพียงแค่ว่ามันต้องปรากฏก่อน $QK$ จึงทำให้ $J$ มีความน่าจะเป็นหนึ่งในสามที่จะถูกเก็บขึ้นมือ

ไล่ตามแนวคิดนี้ไปเรื่อยๆ จึงสรุปได้ว่าไพ่ใบที่มีค่า $r$ จะถูกหยิบด้วยความน่าจะเป็น $\frac1{1+n-r}$ เพราะต้องหลบไพ่ใบอื่นๆ ที่มีค่ามากกว่ามันเป็นจำนวน $n-r$ ใบเพื่อมาปรากฏก่อนนั่นเอง

ผลพลอยได้ก็คือค่าคาดหวังของจำนวนไพ่บนมือ ซึ่งคำนวณได้ว่าคือ $1+\frac12+\frac13+\cdots+\frac1{13} \approx 3.18$ ใบ

---

งั้นกลับไปที่คำถามเวอร์ชันพิมพ์ผิด ว่าความน่าจะเป็นของการเก็บไพ่บนมือได้ $r$ ใบหลังไล่เปิดไพ่จนหมดกองเป็นเท่าไหร่? เราจะเริ่มอธิบายมันผ่านความสัมพันธ์เวียนเกิด $s$ ที่จะนับวิธีที่แตกต่างกันที่จะหยิบไพ่จำนวน $r$ ใบพอดีขึ้นมือ เมื่อเริ่มจากกองไพ่ขนาด $n$ ใบ

\[\begin{align} s(0,0) &= 1 \\ s(n,r) &= \underbrace{s(n-1,r-1)}_\text{CREATE} + \underbrace{(n-1)\,s(n-1,r)}_\text{APPEND} \\ \end{align}\]

โดยแต่ละพจน์ที่เรียกการเวียนเกิด มีรายละเอียดดังนี้

• CREATE: จาก $s(n-1,r-1)$ ที่บอกว่าเคยเปิดไพ่ $n-1$ ใบและหยิบขึ้นมือแล้ว $r-1$ ใบ ดังนั้นไพ่ใบใหม่จะต้องถูกหยิบขึ้นมือเท่านั้นเพื่อรับประกันว่าตอนจบจะมีไพ่ $r$ ใบตามต้องการ ซึ่งก็ทำได้แค่วิธีเดียวคือไพ่ใบสุดท้ายที่เปิดนี้จะต้องมีค่าสูงกว่าไพ่ทุกใบที่เคยเห็นมาทั้งหมด
• APPEND: จาก $s(n-1,r)$ ที่บอกว่าเคยเปิดไพ่ $n-1$ ใบแต่หยิบขึ้นมือมาครบแล้ว $r$ ใบ นั่นทำให้ไพ่ใบใหม่ที่เปิดต้องมีค่าน้อยกว่าใบที่มีค่าสูงที่สุดที่เคยเห็นมา เนื่องจากเรามีไพ่ทั้งหมด $n$ ใบ (อย่าลืมรวมใบที่กำลังจะเปิดด้วย) แต่ไพ่ที่มีค่าสูงสุดมีอยู่เพียงแค่ใบเดียว ดังนั้นไพ่ใบสุดท้ายนี้จึงมีวิธีหยิบแตกต่างกันได้ถึง $(n-1)$ แบบเลยทีเดียว

หน้าตาสมการเวียนเกิดดูคุ้นๆ … ซึ่งถ้าใครคลุกคลีกับเรื่องการนับ ก็คงจะบอกได้ทันทีว่านี่มันคือตัวเลข Stirling ประเภทที่หนึ่งอย่างไม่มีผิดเพี้ยนเลยนั่นเอง!

แต่คำอธิบายมาตฐานของตัวเลข Stirling ประเภทที่หนึ่งนั้นกล่าวว่ามันคือจำนวนวิธีสลับของ $n$ ชิ้นให้ได้ $r$ วัฏจักร … แล้วมันมาเกี่ยวอะไรกับการหยิบไพ่ขึ้นมือตามกฏนี้หละ???

จริงๆ ถ้าเรามองลำดับการหยิบไพ่เป็นการนิยามวัฏจักรของการสับเปลี่ยน โดยเริ่มวัฏจักรใหม่เมื่อเจอไพ่ใบต้องหยิบขึ้นมือ (และเพิ่มไพ่ลงในวัฏจักรล่าสุดที่มีเมื่อไม่หยิบไพ่ขึ้นมือ) เช่น จากตัวอย่างในรูปเมื่อต้นบทความ เราอาจเปลี่ยนไปเขียนมันในรูปกลุ่มวัฏจักรสับเปลี่ยนได้ว่า

\[\pi = (3)(64)(JX78)(K25QA9)\]

จะเห็นได้ชัดว่ากฏการหยิบไพ่เช่นนี้มีค่าเทียบเท่าได้กับตัวเลข Stirling ประเภทที่หนึ่งนั่นเอง

และจาก $\sum_{r=0}^n s(n,r) = n!$ จึงทำให้ได้ความน่าจะเป็นของการหยิบไพ่ได้ $r$ ใบคือ $s(n,r)/n!$