สามเหลี่ยมปัสกาลนั้นเป็นเครื่องมือสุดเรียบง่ายที่ใครก็สามารถคำนวณมันได้ แต่มันกลับมีประโยชน์สารพัดจนเอาไปประยุกต์ใช้ได้ในหลายต่อหลายเรื่อง ซึ่งหนึ่งในเรื่องที่เห็นได้ชัดก็คือการกระจายทวินาม $(a+b)^n$ เมื่อ $n$ เป็นจำนวนเต็มไม่ติดลบ ที่ทำให้เราได้สัมประสิทธิ์ทวินามหลังการกระจายแต่ละพจน์ ว่าพวกมันเหล่านั้นมาจากแถวแนวนอนแถวที่ $n$ ในสามเหลี่ยมนั่นเอง (เริ่มนับแถวแรกว่าเป็นแถวที่ศูนย์)

\[\newcommand{\term}[2]{\underset{\color{red}#2}{\color{black}#1}} \begin{array}{c} \color{blue}\underline{ \term{1}{a^0b^0} }\\ \color{blue}\underline{ \term{1}{a^1b^0} \quad \term{1}{a^0b^1} }\\ \color{blue}\underline{ \term{1}{a^2b^0} \quad \term{2}{a^1b^1} \quad \term{1}{a^0b^2} }\\ \color{blue}\underline{ \term{1}{a^3b^0} \quad \term{3}{a^2b^1} \quad \term{3}{a^1b^2} \quad \term{1}{a^0b^3} }\\ \color{blue}\underline{ \term{1}{a^4b^0} \quad \term{4}{a^3b^1} \quad \term{6}{a^2b^2} \quad \term{4}{a^1b^3} \quad \term{1}{a^0b^4} }\\ \color{blue}\underline{ \term{1}{a^5b^0} \quad \term{5}{a^4b^1} \quad \term{10}{a^3b^2} \quad \term{10}{a^2b^3} \quad \term{5}{a^1b^4} \quad \term{1}{a^0b^5} } \end{array}\]

สามเหลี่ยมปัสกาล (ตัวเลขสีดำ) ซึ่งเป็นสัมประสิทธิ์ที่กำกับการกระจายทวินาม (พจน์สีแดง) ในแต่ละชั้น

แม้การคำนวณค่าสัมประสิทธิ์ทวินามจะทำได้โดยง่ายผ่านการหาผลรวมของสองพจน์ที่ติดกันในแถวก่อนหน้า แต่เราก็ยังสามารถคำนวณในอีกทางหนึ่งซึ่งเป็นเรื่องที่สัมพันธ์แนบแน่นไปกับคณิตศาสตร์เชิงการจัดได้ด้วย คือ สำหรับพจน์ที่มี $a^rb^{n-r}$ ในการกระจาย จะมีสัมประสิทธิ์เป็น $\binom{n}{r}$ โดยที่

\[\binom{n}{r} = \frac{n!}{r!(n{-}r)!}\]

หรือในอีกแง่หนึ่ง หากเปลี่ยนไปเขียนเป็น $a^\alpha b^\beta$ ก็จะได้ว่าสัมประสิทธิ์คือ $(\alpha{+}\beta)!/\alpha!\beta!$ นั่นเอง และถ้าจะให้คลีนกว่านั้น ก็คือระลึกว่า $\alpha{+}\beta=n$ ซึ่งทำให้เราเขียนแค่ $n!/\alpha!\beta!$ ได้อีกด้วย

ตรีนาม

แล้วถ้าเราต้องการกระจายอะไรที่มันมากกว่าทวินามหละ? เช่นเปลี่ยนไปกระจายตรีนาม $(a+b+c)^n$ เราจะคำนวณสัมประสิทธิ์อะไรแบบนี้ได้อยู่หรือเปล่า? สังเกตว่า $(a+b+c)^n = ((a+b)+c)^n$ ซึ่งทำให้เราค่อยๆ แกะพจน์ $c^\gamma$ แยกออกมาก่อน แล้วค่อยกระจายเจ้า $(a+b)^{n-\gamma}$ ที่เหลือได้ในทำนองเดิม หลังจากกระจายเสร็จแล้วจะเห็นว่าพจน์ที่มี $a^\alpha b^\beta c^\gamma$ แปะอยู่นั้นมีสัมประสิทธิ์เป็น $\binom{n}{\alpha,\beta,\gamma}$ เมื่อ

\[\binom{n}{r_1,r_2,\cdots,r_k} = \frac{n!}{r_1! r_2! \cdots r_k!}\]

โดยที่ $\sum_{i=1}^k r_i = n$ นี่คือสัมประสิทธิ์การกระจายอเนกนาม ซึ่งเป็นรูปทั่วไปของสัมประสิทธิ์ทวินามนั่นเอง

คำถามที่น่าสนใจก็คือ ถ้าเราขี้เกียจคำนวณการคูณหารแฟคทอเรียล เราจะกลับไปใช้แค่การบวกธรรมดาๆ แบบที่ทำในสามเหลี่ยมปัสกาลเหมือนเดิมได้มั้ย?

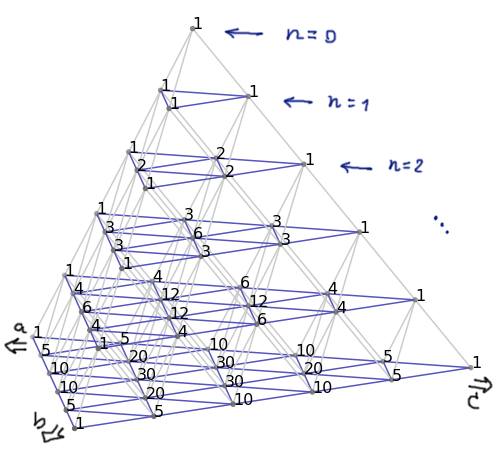
… สามเหลี่ยมปัสกาลตรงๆ คงช่วยไม่ได้ แต่ถ้าเราขยายสามเหลี่ยมปัสกาลที่อยู่ในสองมิติออกไปให้กลายเป็นพีระมิดปัสกาล (เตตระฮีดรอนปัสกาล) ในสามมิติ โดยมองพีระมิดเป็นชั้นๆ แต่ละชั้นมองค่า $n$ เป็นค่าคงตัว และให้กฎการสร้างชั้นใหม่ว่าเป็นการก๊อปปี้ชั้นก่อนหน้าออกมาสามชุด แต่ละชุดขยับไปในทิศทางที่หนีออกจากกันหนึ่งขยัก แล้วจึงจับค่าที่มีตำแหน่งตรงกันมาหาผลรวมเพื่อสร้างแต่ละตำแหน่งในชั้นใหม่นั่นเอง

พีระมิดปัสกาล แบ่งชั้นๆ โดยแต่ละชั้นมอง $n$ เป็นค่าคงตัว¹

ข้อดีของการแบ่งชั้นแบบนี้ คงจะเป็นว่าเราสามารถสไลซ์แต่ละชั้นออกมาดูแล้วมีความหมาย นั่นคือแต่ละชั้นมันจะบอกเลยว่าให้ค่าสัมประสิทธิ์เป็นเท่าไหร่บ้างสำหรับแต่ละพจน์ในการกระจายตรีนาม

\[\begin{array}{c} \color{#ffff}\underline{ \term{1}{a^5b^0c^0} }\\ \color{#ffff}\underline{ \term{5}{a^4b^1c^0} \quad \term{5}{a^4b^0c^1} }\\ \color{#ffff}\underline{ \term{10}{a^3b^2c^0} \quad \term{20}{a^3b^1c^1} \quad \term{10}{a^3b^0c^2} }\\ \color{#ffff}\underline{ \term{10}{a^2b^3c^0} \quad \term{30}{a^2b^2c^1} \quad \term{30}{a^2b^1c^2} \quad \term{10}{a^2b^0c^3} }\\ \color{#ffff}\underline{ \term{5}{a^1b^4c^0} \quad \term{20}{a^1b^3c^1} \quad \term{30}{a^1b^2c^2} \quad \term{20}{a^1b^1c^3} \quad \term{5}{a^1b^0c^4} }\\ \color{#ffff}\underline{ \term{1}{a^0b^5c^0} \quad \term{5}{a^0b^4c^1} \quad \term{10}{a^0b^3c^2} \quad \term{10}{a^0b^2c^3} \quad \term{5}{a^0b^1c^4} \quad \term{1}{a^0b^0c^5} } \end{array}\]

ตัวอย่างการกระจายตรีนามซึ่งเป็นสไลซ์ชั้นหนึ่งจากพีระมิดข้างต้นที่ให้ $n=5$ เป็นค่าคงตัว

แต่ข้อเสียก็คงจะเป็นเมื่อเราหยิบสไลซ์หนึ่งๆ มาดูแล้ว มันอาจจะยากมากที่จะหาความสัมพันธ์ของตัวเลขเหล่านั้นได้² ไม่เหมือนกับตอนที่เป็นสามเหลี่ยมปัสกาลที่ตรงไปตรงมามองออกทันทีว่ามันคือการบวกกัน

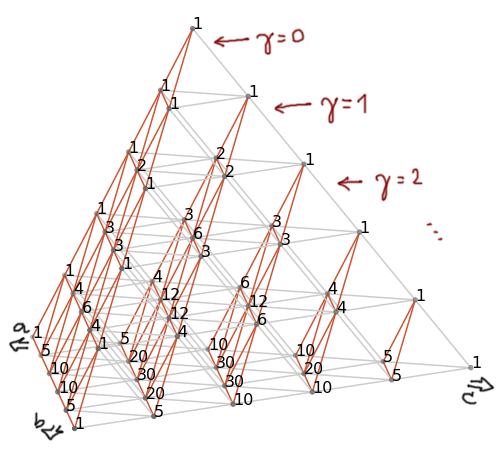
อย่างไรก็ตาม ถ้าเราเลือกสไลซ์พีระมิดในอีกแนวหนึ่งแทน อย่างเช่นเปลี่ยนไปมองค่า $\gamma$ (ในพจน์ $c^\gamma$) เป็นค่าคงตัวในแต่ละชั้น เราจะได้สไลซ์อันสุดแสนจะคุ้นเคยกลับออกมา

พีระมิดปัสกาล คราวนี้แบ่งชั้นโดยไม่มอง $n$ เป็นค่าคงตัวแล้ว

จะเห็นว่าสไลซ์ซ้ายสุดที่ $\gamma=0$ นั้นคือสามเหลี่ยมปัสกาลตัวตั้งต้นเลย … น่าเสียดายว่าสไลซ์อื่นๆ ยังได้สามเหลี่ยมหน้าตาแปลกประหลาดที่มองความสัมพันธ์ยากกลับออกมาอยู่ดี³

สังเกตว่าเมื่อเราเลือกสไลซ์เช่นนี้ แต่ละสไลซ์จะเป็นสามเหลี่ยมที่ใหญ่เป็นอนันต์แล้ว (นั่นคือ มีแถวด้านล่างเพิ่มได้เรื่อยๆ ไม่รู้จบ) ต่างจากก่อนหน้าที่เราสไลซ์โดยให้ $n$ เป็นค่าคงตัว แต่ละสไลซ์จึงมีขนาดจำกัดนั่นเอง

จตุนาม

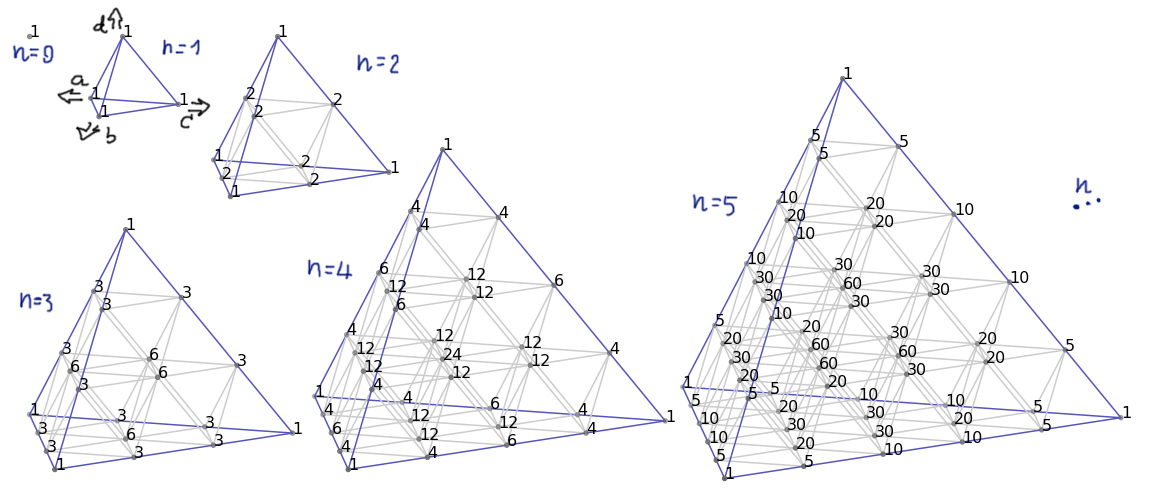
ในพีระมิดสามมิติที่เราสไลซ์โดยให้ $\gamma$ เป็นค่าคงตัว เราได้เห็นผลลัพธ์สไลซ์สองมิติที่หน้าตัดหน้าหนึ่งเป็นสามเหลี่ยมปัสกาลพอดิบพอดีไปแล้ว เช่นนี้ก็น่าจะเดาได้ไม่ยากว่า ตัวพีระมิดปัสกาลทั้งอันนั้นก็คือสไลซ์จากอะไรซักอย่างในมิติที่สูงกว่า

ซึ่งไอ้อะไรซักอย่างที่ว่านี้เราเรียกมันว่าซิมเพล็กซ์ อธิบายอย่างง่ายๆ คือมันเป็นรูปทรงที่แต่ละจุดยอดนั้นเชื่อมไปยังจุดยอดอื่นๆ ทุกจุดด้วยระยะทางเท่ากัน และหากเรานำตัวเลขในทำนองเดียวกับที่ผ่านมาไปใส่ให้มันก็จะทำให้เราได้ซิมเพล็กซ์ปัสกาลนั่นเอง

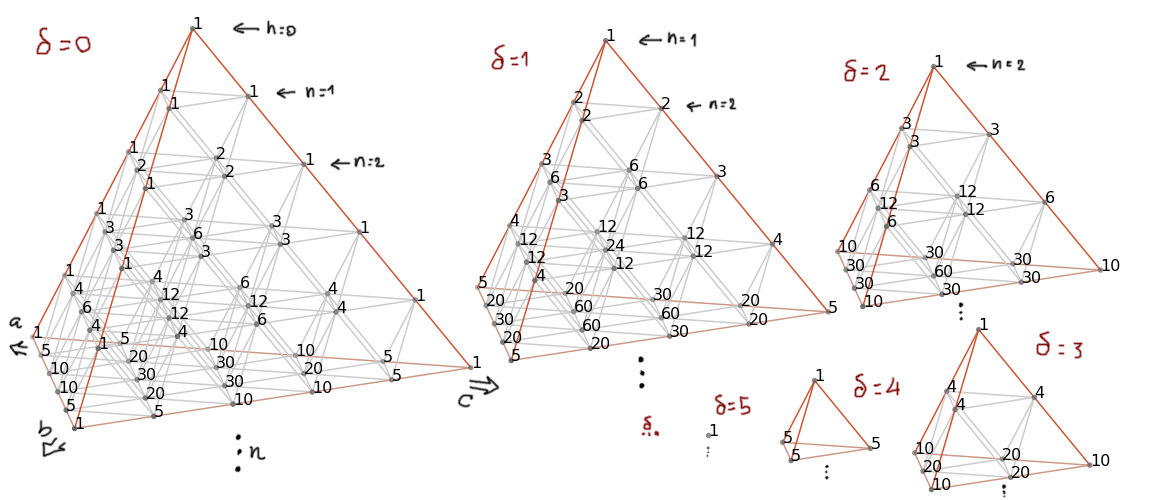
สำหรับการกระจายจตุนาม $(a+b+c+d)^n$ จะใช้ซิมเพล็กซ์ตัวที่ใหญ่ถัดไปจากพีระมิดในสามมิติ นั่นก็คือเพนตะโทป⁴ในสี่มิติ … ซึ่งเราคงจินตนาการมันไม่ออก แต่ถ้าเราสไลซ์โดยมอง $\delta$ เป็นค่าคงตัว ก็จะได้สไลซ์แต่ละชิ้นเป็นพีระมิด เช่นนี้

เพนตะโทปปัสกาล สไลซ์ออกมาเป็นพีระมิดหลายๆ ชิ้น แต่ละชิ้นมีขนาดเป็นอนันต์

แน่นอนว่าสไลซ์ซ้ายสุดที่ $\delta=0$ นั้นดูรู้เรื่อง เพราะเราผูกพันธ์กับมันจากภาพพีระมิดปัสกาลในสามมิติไปแล้ว อย่างไรก็ตาม ถ้าเราเปลี่ยนไปสไลซ์ด้วยการมอง $n$ เป็นค่าคงตัวแทน (ทำนองเดียวกับตอนสไลซ์พีระมิด) มันคงจะมีประโยชน์กว่าเมื่อเราเอาไปใช้งานกับเรื่องการจัด

เพนตะโทปปัสกาล สไลซ์เป็นพีระมิดหลายๆ ชิ้น แต่ละชิ้นมอง $n$ เป็นค่าคงตัว

สำหรับมิติที่สูงยิ่งขึ้นไปอีกแม้เราจะจินตนาการตามไม่ไหวแล้ว แต่ด้วยเทคนิคสไลซ์ภาพออกมาดูในมิติที่เราคุ้นเคย ก็น่าจะช่วยให้เราพอจะทำความเข้าใจพวกมันได้อยู่ (มั้ง)

หรืออีกทางที่ออกจะแห้งแล้งหน่อยๆ ก็คือเลิกคิดภาพว่าจะมองพวกมันยังไงไปเลย แล้วมาสนใจแค่สมการ $\binom{n}{r1,r_2,\cdots,r_k}$ ที่สรุปออกมาก็พอ 🤔