แฟร็กทัลตัวหนึ่งที่เรียบง่าย แล้วก็ซับซ้อน แล้วก็กลับมาเรียบง่าย แต่ก็ยังไม่ทิ้งลายความซับซ้อน คงหนีไม่พ้นเซต Cantor แบบสามส่วน ซึ่งมันเป็นเซตของจำนวนจริงในช่วงปิด $[0,1]$ ที่เขียนนิยามผ่านความสัมพันธ์เวียนเกิดได้ว่า

\[\begin{align} C_0 &= [0,1] \\ C_n &= \frac{C_{n-1}}3 \cup \left( \frac23 + \frac{C_{n-1}}3 \right) \end{align}\]

โดยตัวเซต Cantor จริงๆ แล้วนั้นจะเป็นเซตปลายทางเมื่อเราดำดิ่งลงไปในความสัมพันธ์เวียนเกิดข้างต้นอย่างไม่รู้จบ ซึ่งก็คือ

\[\mathcal{C} = \lim_{n \to \infty} C_n\]

มองเป็นสมการอาจไม่น่าตื่นตาตื่นใจเท่าไหร่ (หรืออาจถึงขั้นเห็นไม่ชัดเลยว่ามันจะเป็นแฟร็กทัลยังไงด้วย) แต่ถ้าได้ลองวาดรูปบนเส้นจำนวนดูก็น่าจะเห็นภาพอย่างชัดเจน ว่ามันก็คือการลบกล่องสี่เหลี่ยมตรงกลางขนาดความกว้าง $1/3$ ทิ้งไปเรื่อยๆ นั่นเอง

ซูมดู $C_n$ ให้ลึกลงไป – สัดส่วนการซูมในแกนตั้งกับแกนนอนนั้นไม่เท่ากัน

มันจะมีรายละเอียดปลีกย่อยทางเทคนิคเล็กๆน้อยๆ อย่างเช่นว่าเราเริ่มด้วยกล่องสี่เหลี่ยมที่เป็นช่วงปิด (รวมค่าสุดขอบที่หัวท้าย) แต่ตอนลบช่วงตรงกลางนั้นเราลบด้วยช่วงเปิด (ไม่รวมขอบหัวท้าย) ดังนั้นหลังจากลบเสร็จ เราจะได้ช่วงปิดสองช่วงกลับมา นี่ทำให้ท้ายที่สุดแล้ว $\mathcal{C}$ จะกลายเป็นเซตของจำนวนจริงโดดๆ ไม่ได้เป็นเซตของช่วงที่ต่อเนื่องกันแบบ $C_n$ อีกต่อไป

ซึ่งเราน่าจะเห็นได้ชัดผ่านการเขียนค่าสมาชิกใน $\mathcal{C}$ ออกมาเป็นจำนวนจุดลอยตัว ที่ทำได้กฎอันเรียบง่ายเมื่อเขียนด้วยเลขฐานสาม ที่มีข้อจำกัดว่าค่าประจำตำแหน่งหลักสามารถเป็นได้แค่ $0_3$ หรือ $2_3$ เท่านั้น เช่น

\[\begin{align} 2/3 &= (0.2)_3 \\ 1/3 &= (0.022222\dots)_3 = (0.\overline{2})_3 = (0.1)_3 \end{align}\]

แต่ความน่าตื่นตาตื่นใจยิ่งกว่า ก็คือแม้ว่า $\mathcal{C}$ จะเป็นเซตของเลขจำนวนจริงโดดๆ อย่างไรก็ดี หากจับสมาชิกสองตัว (ซ้ำกันได้) ในเซตมาบวกกันแล้ว มันสามารถสร้างจำนวนจริงกลับมาได้ทุกตัวในช่วง $[0,2]$ เลยทีเดียว

พูดอีกอย่างก็คือ

\[\mathcal{C} \oplus \mathcal{C} = [0,2]\]

โดยนิยามการบวกระหว่างเซตว่า $A \oplus B = \lbrace a+b \;|\; a \in A, b \in B \rbrace$

ซึ่งอาจพิสูจน์ให้เห็นได้สวยๆ ผ่านการอุปนัย ที่ย้อนกลับไปเอา $C_n$ เข้ามาช่วย โดยเริ่มจาก

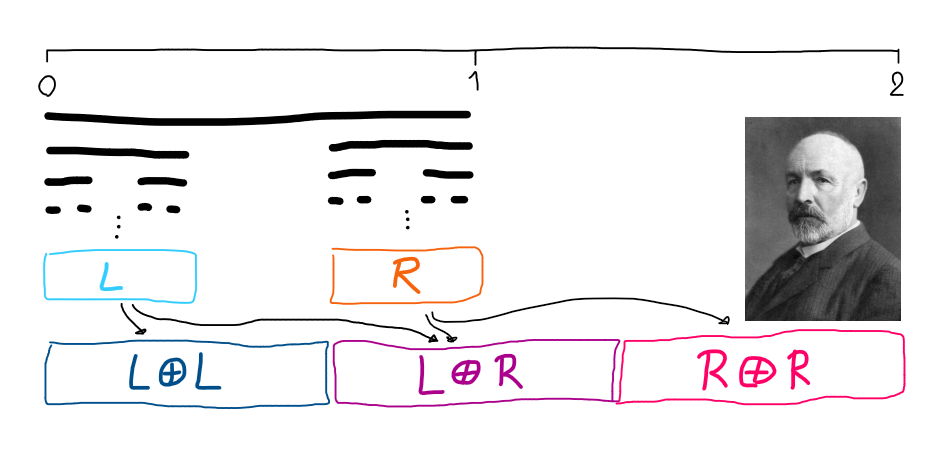
\[\begin{align} C_n &= L \cup R \\ L &= \frac{C_{n-1}}3 \\ R &= \frac23 + \frac{C_{n-1}}3 \end{align}\]

แล้วหลังจากนั้น

\[\begin{align} C_n \oplus C_n &= (L \cup R) \oplus (L \cup R) \\ &= (L \oplus L) \cup (L \oplus R) \cup \cancel{(R \oplus L)} \cup (R \oplus R) \\ &= \frac13 \Big( (C_{n-1} \oplus C_{n-1}) \cup (2 + C_{n-1} \oplus C_{n-1}) \cup (4 + C_{n-1} \oplus C_{n-1}) \Big) \\ &= \frac13\Big( [0,2] \cup [2,4] \cup [4,6] \Big) = [0,2] \end{align}\]

แน่นอนว่าวาดภาพออกมาน่าจะช่วยให้เห็นคอนเซปต์ได้ง่ายกว่า(?)

บทพิสูจน์ด้วยการแปะภาพคนดัง 😜

ความเจ๋งจากแนวทางการอุปนัยเช่นนี้ คือเราสามารถประยุกต์ใช้มันเพื่อหาว่าสำหรับแต่ละ $x \in [0,2]$ เราสามารถแยกมันเป็น $x=a+b$ โดยที่ $a,b \in \mathcal{C}$ ได้อย่างไร

ซึ่งก็คือเราจะค่อยๆ แกะค่าออกมาโดยเริ่มจาก $a,b \in C_1$ ว่าต้องใช้ค่าจากฝั่ง $L$ หรือ $R$ มาบวกกันเพื่อสร้าง $x$ หลังจากนั้นจะบีบให้ $a,b$ ละเอียดเล็กลงเรื่อยๆ ด้วยการพิจารณา $C_n$ ที่สูงขึ้นไป

สรุปเป็นอัลกอริทึมโดยเริ่มที่ $x_1 \gets x$ ได้ประมาณนี้

1. พิจารณาว่า $x_i$ อยู่ในช่วงใด แล้วทดค่าเก็บไว้ในรูปของ $A_i \oplus B_i$
   • หาก $x_i \in [0,2/3)$ ทดค่า $L \oplus L$
   • หาก $x_i \in [2/3,4/3)$ ทดค่า $L \oplus R$
   • หาก $x_i \in [4/3,2)$ ทดค่า $R \oplus R$
2. คำนวณ $x_{i+1} \gets 3x_i \pmod{2}$
3. เพิ่มค่า $i$ แล้วย้อนกลับไปทำข้อ 1. ไล่มาเรื่อยๆ จนกว่าจะเหนื่อย

เหนื่อยแล้วจะได้ลิสต์ $[A_1 \oplus B_1, A_2 \oplus B_2, A_3 \oplus B_3, \dots]$ กลับมา ซึ่งเอาไปสร้าง $x=a+b$ ได้เป็น

\[\begin{align} a &= A_1A_2A_3\dots \\ b &= B_1B_2B_3\dots \end{align}\]

หลังจากนั้นแปลงเป็นจำนวนจุดลอยตัวในฐานสาม โดยให้ $L=0$ และ $R=2$ ก็จะได้คำตอบที่ต้องการ

ตัวอย่างเช่น $x=1/2$ เราแกะค่าออกมาได้ดังนี้

\[\begin{array}{c|cc} i & 1 & 2 & 3 & 4 & \dots \\ \hline x_i & 1/2 & 3/2 & 1/2 & 3/2 & \dots \\ A_i \oplus B_i & L \oplus L & R \oplus R & L \oplus L & R \oplus R & \dots \end{array}\]

ดังนั้นจึงหา $x=a+b$ ได้เป็น

\[\begin{align} a &= LRLR\dots = (0.0202\dots)_3 = (0.\overline{02})_3 = 1/4 \\ b &= LRLR\dots = (0.0202\dots)_3 = (0.\overline{02})_3 = 1/4 \end{align}\]

หมายเหตุว่าอัลกอริทึมดังกล่าวไม่จำเป็นต้องให้คำตอบเพียงแค่วิธีเดียวที่เป็นไปได้ ลองดูตัวอย่างเมื่อต้องการ $x=11/27$

\[\begin{array}{c|cc} i & 1 & 2 & 3 & 4 & 5 & \dots \\ \hline x_i & 11/27 & 11/9 & 5/3 & 1 & 1 & \dots \\ A_i \oplus B_i & L \oplus L & L \oplus R & R \oplus R & L \oplus R & L \oplus R & \dots \end{array}\]

ที่อาจให้คำตอบแรกอันเรียบง่ายกลับมาว่า

\[\begin{align} a &= LLRLLL\dots = (0.002)_3 = 2/27 \\ b &= LRRRRR\dots = (0.0222\dots)_3 = (0.0\overline{2})_3 = (0.1)_3 = 1/3 \end{align}\]

แต่เพราะการบวกมีสมบัติสลับที่ ดังนั้นค่าที่จดไว้ว่า $L \oplus R$ มันไม่ได้หมายถึงแค่ $A_i=L, B_i=R$ เพียงเท่านั้น แต่ยังสามารถหมายถึง $A_i=R,B_i=L$ ได้อีกด้วย และทำให้เราได้คำตอบอื่นๆ อีกมากมาย เช่น

\[\begin{align} a &= LRRLLL\dots = (0.022)_3 = 8/27 \\ b &= LLRRRR\dots = (0.0022\dots)_3 = (0.00\overline{2})_3 = (0.01)_3 = 1/9 \end{align}\]

หรือแม้กระทั่ง

\[\begin{align} a &= LLRLRLRLR\dots = (0.0\overline{02})_3 = 1/12 \\ b &= LRRRLRLRL\dots = (0.022\overline{20})_3 = 35/108 \end{align}\]

ซ.ต.พ.