Code Jam 2018: UFO ลูกบาศก์
สัปดาห์ก่อนเขียนเฉลย Code Jam 2018 รอบคัดเลือกไป ซึ่งก็แอบอู้ไม่อธิบายข้อสุดท้าย เอากระดานที่ทดสมการมาแปะแทน … หลายคนน่าจะแอบด่าในใจไปแล้วว่าอ่านไม่เห็นรู้เรื่องเลย 555 งั้นตอนนี้ขอแก้ตัวอธิบายวิธีทำข้อ Cubic UFO อย่างละเอียดละกันครับ
แนวคิดพื้นฐาน
สังเกตว่าลูกบาศก์ 3 มิติ เมื่อฉายเงา (projection) ลงมาใน 2 มิติ คือการตัดค่าตำแหน่งในแกนตั้งออกไปนั่นเอง (โจทย์ข้อนี้กำหนดให้แกนตั้งคือแกน Y … น่าแปลกใจมากว่าทำไมไม่ใช้แกน Z กำหนดแบบนี้แล้วเห็นมีคนพลาดตั้งหลายคน)
ดังนั้นลูกบาศก์หนึ่งหน่วยที่อยู่นิ่งๆ ยังไม่ได้หมุนอะไร ก็จะมีจุดยอดของเงาอยู่ 4 จุด (มีทั้งหมด 8 จุดแต่ซ้ำกันไปซะครึ่ง) ได้แก่
\[\lbrace (\pm0.5, \pm0.5) \rbrace = \lbrace (0.5, 0.5), (0.5, -0.5), (-0.5, 0.5), (-0.5, -0.5) \rbrace\]เกิดเป็นเงารูปสี่เหลี่ยมจัตุรัส มีขนาดพื้นที่เป็น 1 ตารางหน่วย
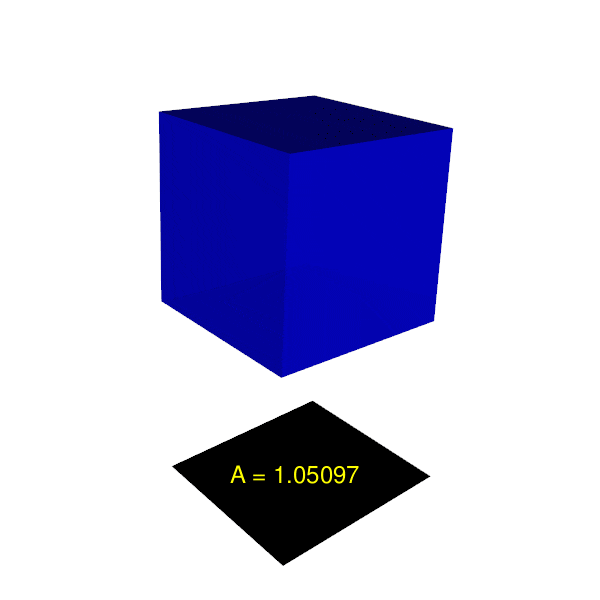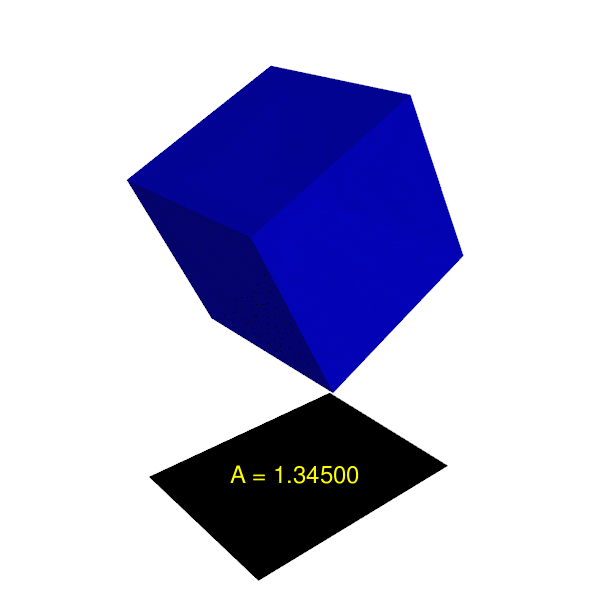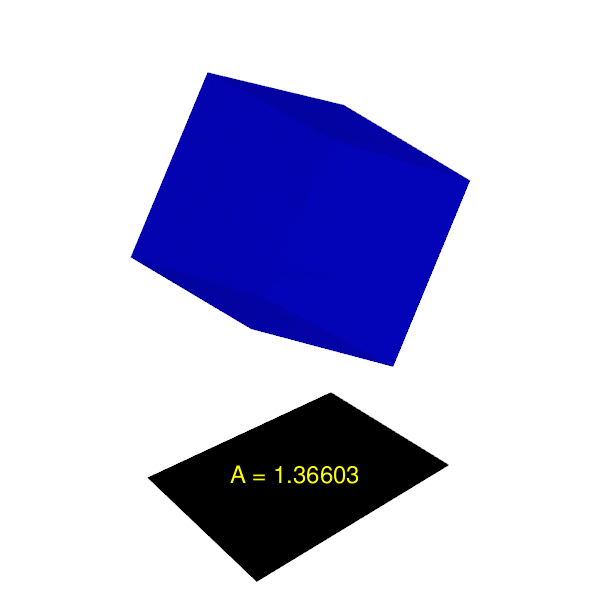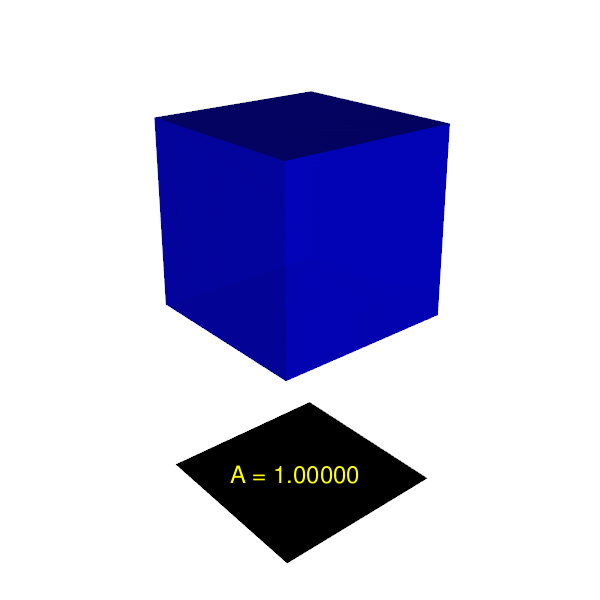
ทีนี้เมื่อเราหมุนลูกบาศก์ตามแกน X จะเห็นว่ารูปร่างเงาเปลี่ยนไปเป็นสี่เหลี่ยมผืนผ้า ดังภาพประกอบที่ 1
ภาพที่ 1: พื้นที่เงาต่างๆ เมื่อหมุนลูกบาศก์ตามแกน X เพียงแกนเดียว1
พื้นที่สี่เหลี่ยมผืนผ้าที่ได้เมื่อหมุนลูกบาศก์ จะมีขนาดตั้งแต่ 1 ถึง $\sqrt{2}$ ตารางหน่วย โดยลูกบาศก์ต้องถูกหมุนไป 45 องศาพอดีเพื่อให้มีพื้นที่มากที่สุด หากอนุญาตให้หมุนแค่แกน X แกนเดียว
แต่เรื่องสุดสนุกกำลังจะเกิดขึ้นเมื่อเราเริ่มหมุนแกนที่สองหลังจากหมุนแกนแรกจนได้พื้นที่มากที่สุดไปแล้ว … แน่นอนคำถามที่ตามมาคือ แล้วจะหมุนแกนไหนดีหละ?
หากเราหมุนแกน Y ก็จะได้ผลลัพธ์ตามภาพประกอบที่ 2 นี้
ภาพที่ 2: พื้นที่เงาต่างๆ เมื่อหมุนลูกบาศก์ตามแกน Y หลังจากหมุนแกน X ไปแล้ว 45 องศา
น่าจะเห็นชัดแล้วว่าการหมุนตามแกน Y ไม่ช่วยอะไรเลย!
ส่วนการหมุนตามแกน Z ให้ผลลัพธ์ตามภาพประกอบที่ 3
ภาพที่ 3: พื้นที่เงาต่างๆ เมื่อหมุนลูกบาศก์ตามแกน Z หลังจากหมุนแกน X ไปแล้ว 45 องศา
พื้นที่เงาที่มีขนาดใหญ่ที่สุด เกิดขึ้นเมื่อหมุนลูกบาศก์ตามแกน X ไป 45 องศา แล้วจึงหมุนตามแกน Z ไปอีก $\arctan\frac{1}{ \sqrt{3} }$ (หรือประมาณ 35.26) องศา ซึ่งให้ขนาดเงาเป็นรูปหกเหลี่ยมด้านเท่า ที่ขนาด $\sqrt{3}$ ตารางหน่วย
ถึงตอนนี้ถ้าเรารู้จักอัลกอริทึม binary search, convex hull, shoelace formula, และ rotation matrix ก็สามารถแก้ไขปัญหานี้ได้แล้วด้วยโค้ดเทียมต่อไปนี้
CONSTANTS:
corners = { (+-0.5, +-0.5, +-0.5) }
faces = { (0.5, 0, 0), (0, 0.5, 0), (0, 0, 0.5) }
FUNCTION binary_search(corners, area, lower, upper):
LOOP:
angle = (lower+upper)/2
points = rotate_x(corners, angle)
points_on_plane = projection_xz(points)
corners_on_plane = convex_hull(points_on_plane)
guess_area = shoelace(corners_on_plane)
IF guess_area < area:
lower = angle
ELSE IF guess_area > area:
upper = angle
ELSE:
RETURN angle
FUNCTION solve():
READ FLOAT required_area
IF 1 <= required_area <= sqrt(2):
angle = binary_search(corners, required_area, 0, 45)
out_faces = rotate_x(faces, angle)
ELSE IF sqrt(2) < required_area <= sqrt(3):
tmp_corners = rotate_x(corners, 45)
angle = binary_search(tmp_corners, required_area, 0, atan(1/sqrt(2)))
tmp_faces = rotate_x(faces, 45)
out_faces = rotate_z(tmp_faces, angle)
PRINT out_faces
หามุมที่ใช่โดยไม่ต้องแบ่งเคสการหมุน
ในภาพประกอบที่ 3 ตอนแรกเราสนใจแค่ต่อยอดการหมุนจากแกน X ไปหาพื้นที่สูงสุด แล้วเขียนคำตอบโดยแบ่งเคสเอาว่าเมื่อไหร่ที่การหมุนแกน X แค่แกนเดียวยังได้พื้นที่น้อยกว่าที่ต้องการ ก็ค่อยไปหมุนแกน Z เพิ่ม
แต่หากเราพิจารณาการหมุนทั้งหมด จะเห็นว่าพื้นที่เงามันครอบคลุมพื้นที่ตั้งแต่ช่วง 1 ถึง $\sqrt{3}$ เช่นกัน นี่หมายความว่าเราไม่จำเป็นต้องแบ่งคิดเป็นช่วงๆ ก็ได้ แต่เปลี่ยนวิธีคิดเป็นดังนี้
เริ่มจากหมุนลูกบาศก์ตามแกน Y ไป 45 องศา (สังเกตว่าตอนนี้พื้นที่ยังเป็น 1 ตารางหน่วย) แล้วต่อมาจึงหาว่าต้องหมุนตามแกน Z (หรือแกน X ก็ได้) อีกกี่องศาจึงจะได้พื้นที่ตามที่ต้องการ
FUNCTION solve():
READ FLOAT required_area
adjust_corners = rotate_y(faces, 45)
angle = binary_search(adjust_corners, required_area, 0, 90-atan(1/sqrt(2)))
tmp_faces = rotate_y(faces, 45)
out_faces = rotate_x(tmp_faces, angle)
PRINT out_faces
ตรีโกณมิติหาคำตอบพอดี
วิธีข้างบนๆ นั้นเขียนเร็วและง่าย (และก็เพียงพอที่จะทำงานทัน) แต่หากลงแรงคิดต่อไปอีกนิด ก็จะพบว่ามีคำตอบที่ไม่ต้อง binary search เช่นกัน
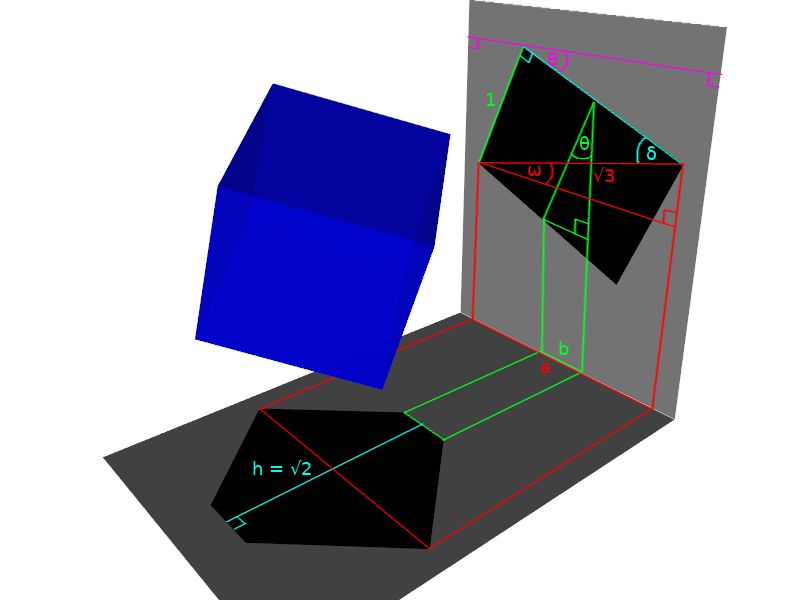
ภาพที่ 4: มุมและความยาวสำคัญต่างๆ สำหรับคำนวณพื้นที่เงา เมื่อหมุนลูกบาศก์ตามแกน Y ไป 45 องศา แล้วหมุนตามแกน Z อีก θ องศา
พิจารณาภาพประกอบที่ 4 จะเห็นว่าเราสามารถคำนวณพื้นที่รูป 6 เหลี่ยมได้โดยตรง โดยไม่ต้องพึ่ง convex hull และ shoelace formula แล้ว ซึ่งก็คือ
\[\begin{align*} A &= bh + (a-b)\frac{h}{2} \\ &= (a+b)\frac{h}{2} \\ &= \frac{ (a+b) }{ \sqrt{2} } \end{align*}\]แต่เนื่องจาก
\[\begin{align*} a &= \sqrt{3}\cos\omega \\ b &= \sin\theta \\ \omega &= \delta-\theta \\ \delta &= \arccos\sqrt{ \frac{2}{3} } = \arcsin\frac{1}{ \sqrt{3} } \end{align*}\]ดังนั้น
\[\begin{align*} A &= \frac{ \sqrt{3}\cos(\delta-\theta) + \sin\theta }{ \sqrt{2} } \\ &= \frac{ \sqrt{3}\cos\delta\cos\theta + \sqrt{3}\sin\delta\sin\theta + \sin\theta }{ \sqrt{2} } \\ &= \frac{ \sqrt{2}\cos\theta + 2\sin\theta }{ \sqrt{2} } \\ &= \sqrt{2}\sin\theta + \cos\theta \end{align*}\]แม้ฝั่งขวาของสมการจะติดฟังก์ชันตรีโกณมิติ 2 ฟังก์ชัน แต่ถ้ายังจำเอกลัษณ์ตรีโกณมิติกันได้ จะพบว่าสามารถจัดรูปให้เป็น
\[\sin(\alpha+\beta) = \sin\alpha \cos\beta + \cos\alpha \sin\beta\]ซึ่งก็คือ
\[\begin{align*} A &= x \left( \frac{ \sqrt{2} }{x} \sin\theta + \frac{1}{x} \cos\theta \right) \\ \sin\gamma &= \frac{1}{x} \\ \cos\gamma &= \frac{\sqrt{2} }{x} \end{align*}\]เพราะฉะนั้น
\[\begin{align*} \tan\gamma &= \frac{1}{ \sqrt{2} } \\ \gamma &= \arctan\frac{1}{ \sqrt{2} } = \arcsin\frac{1}{ \sqrt{3} } \\ x &= \sqrt{3} \end{align*}\]ดังนั้น
\[\begin{align*} A &= \sqrt{3} \left( \cos\gamma\sin\theta + \sin\gamma\cos\theta \right) \\ &= \sqrt{3} \sin(\theta+\gamma) \\ &= \sqrt{3} \sin\left(\theta+\arcsin\frac{1}{ \sqrt{3} }\right) \end{align*}\]และเมื่อหาฟังก์ชันผกผันเพื่อคำนวนมุมจากพื้นที่ ก็จะได้เป็น
\[\theta = \arcsin\frac{A}{ \sqrt{3} } - \arcsin\frac{1}{ \sqrt{3} }\]ซึ่งนำไปเขียนโค้ดเทียมได้สั้นลงเหลือแค่นี้
FUNCTION solve():
READ FLOAT required_area
angle = asin(required_area/sqrt(3)) - asin(1/sqrt(3))
tmp_faces = rotate_y(faces, 45)
out_faces = rotate_z(tmp_faces, angle)
PRINT out_faces
ก็ถือว่าจบการเฉลยในข้อนี้

author