เทคนิคหนึ่งที่น่าสนใจเวลาพยายามแก้โจทย์แนวหาซับเซตจากเซตข้อมูลนำเข้าที่มีขนาด $n$ คือการเริ่มต้นด้วยสมมติฐานที่ว่าเรารู้ขนาดของซับเซตคำตอบไปก่อนเลยว่าเท่ากับ $k$ แล้วสร้างอัลกอริทึมย่อยที่ทำงานได้รวดเร็วขึ้นกับขนาดของคำตอบนั้น ท้ายสุดจึงค่อยกลับไปเดาว่าค่าของ $k$ ที่แท้จริงควรเป็นเท่าไหร่กันแน่

หากเราออกแบบอัลกอริทึมย่อยดีๆ เราอาจได้ว่าอัลกอริทึมที่หาคำตอบที่ขนาด $k$ ได้นั้น สามารถนำไปหาคำตอบที่มีขนาดน้อยกว่า $k$ ได้อีกด้วย (หรือก็คืออัลกอริทึมย่อยดังกล่าว สามารถหาคำตอบได้สำหรับทุกขนาดคำตอบที่ $\le k$) เมื่อเป็นเช่นนี้แล้วเราไม่จำเป็นต้องคิดค้นวิธีพิสดารมาเดาค่า $k$ อีกต่อไป เพราะเราสามารถนำเทคนิคในทำนองเดียวกับการค้นหาแบบทวิภาคมาช่วยหาค่า $k$ ที่ต้องการได้ ดังตัวอย่างต่อไปนี้

สมมติให้อัลกอริทึมย่อยนั้นทำงานได้เร็ว $O(n \log k)$ จะเห็นว่าหากเราทดลองไล่ค่า $k$ จาก $m=1,2,3,\cdots$ ไปเรื่อยๆ อัลกอริทึมจะคืนคำตอบที่ถูกต้องเมื่อ $m=k$ ดังนั้นเวลารวมของอัลกอริทึมจะกลายเป็น

\[\begin{align*} \sum_{i=1}^k O(n \log i) &= O(n \log 1) + O(n \log 2) + O(n \log 3) + \cdots + O(n \log k) \\ &\le \underbrace{O(n \log k) + O(n \log k) + O(n \log k) + \cdots + O(n \log k)}_{k\text{ terms} } \\ &= O(nk \log k) \end{align*}\]

(และถึงแม้ว่าเราจะสามารถเลือก $m=n$ ไปเลยเพื่อให้อัลกอริทึมย่อยทำงานแค่ครั้งเดียว แต่เราจะได้ว่าความเร็วจะกลายเป็น $O(n \log n)$ แทน ทั้งที่จริงๆ แล้วเราสามารถแก้ปัญหาได้เร็วกว่านี้)

ถึงตอนนี้ถ้าเรานำการค้นหาแบบทวิภาคมาประยุกต์ใช้ กล่าวคือแทนที่จะเพิ่มค่า $k$ ครั้งละหนึ่งไปเรื่อยๆ แต่เปลี่ยนไปเพิ่มเป็นสองเท่าของค่าเดิมแทน (ซึ่งก็คือ $m=2,4,8,\cdots$) จะเห็นว่าอัลกอริทึมย่อยหยุดทำงานเมื่อ $m \ge k$ หรือก็คือรอบที่ $t = \lceil \log_2 k \rceil$ ดังนั้นความเร็วของอัลกอริทึมโดยรวมจะเหลือ

\[\begin{align*} \sum_{i=1}^t O(n \log 2^i) &= O(n \log 2) + O(n \log 4) + O(n \log 8) + \cdots + O(n \log 2^t) \\ &\le \underbrace{O(n \log k) + O(n \log k) + O(n \log k) + \cdots + O(n \log k)}_{\lceil \log_2 k \rceil\text{ terms} } \\ &= O(n \log k \log k) \end{align*}\]

จะเห็นว่าเราออกแบบอัลกอริทึมย่อยที่ทำงานได้เร็ว $O(n \log k)$ แต่เนื่องจากเราไม่รู้ค่า $k$ ล่วงหน้า จึงทำให้เวลารวมทั้งหมดยังกลายเป็น $O(n \log k \log k)$ … แล้วเราจะทำให้เร็วกว่านี้ได้อีกหรือเปล่า?

ทริกที่จะมาแก้ปัญหาตรงนี้คือเราต้องกระโดดให้เร็วกว่าเอกซ็โพเนนเชียล คือไม่เพิ่มค่า $m$ แค่ครั้งละสองเท่าเมื่อการค้นหาครั้งก่อนล้มเหลวแล้ว แต่เพิ่มแบบดับเบิลเอกซ์โพเนนเชียลแทน ซึ่งก็คือ

\[\begin{array}{r|cc} i & 1 & 2 & 3 & \cdots & i & \cdots & \lceil \log_2 \log_2 k \rceil \\ \hline m & 4 & 16 & 256 & \cdots & 2^{2^i} & \cdots & \underset{ \text{(round up to double exponential of 2)} }{\lceil k \rceil} \end{array}\]

จะเห็นว่ารอบสุดท้ายคือ $t = \lceil \log_2 \log_2 k \rceil$ ดังนั้นความเร็วของอัลกอริทึมทั้งหมดคือ

\[\begin{align*} \sum_{i=1}^t O(n \log 2^{2^i}) &= O(n \log 4) + O(n \log 16) + O(n \log 256) + \cdots + O(n \log 2^{2^t}) \\ &= O(n \times 2) + O(n \times 4) + O(n \times 8) + \cdots + O(n \times 2^t) \\ &= O(n \times (2 + 4 + 8 + \cdots + 2^t)) \\ &= O(n \times 2^t) \\ &= O(n \log k) \end{align*}\]

สังเกตว่าคราวนี้เราไม่ได้ปัดแต่ละพจน์ขึ้นเป็น $\log k$ แล้ว แต่เขียนเป็นผลรวมอนุกรมเรขาคณิตแทน ทำให้ได้ผลลัพธ์สุดท้ายมาว่าอัลกอริทึมของเราเร็วเป็น $O(n \log k)$ ตามที่ต้องการ

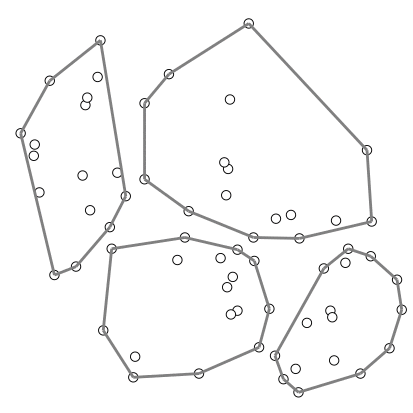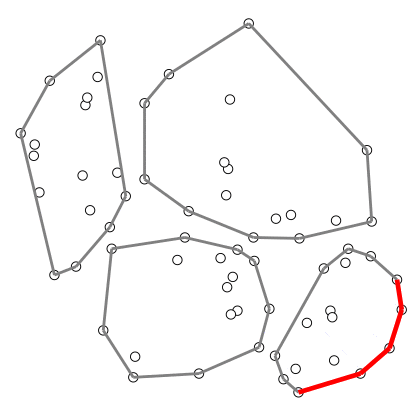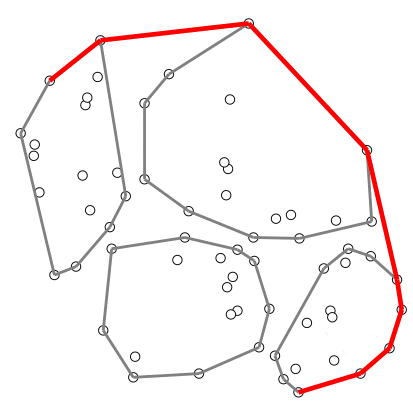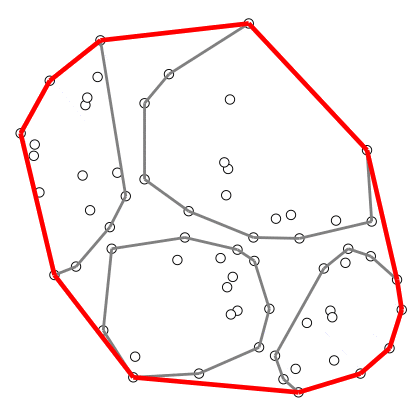
อัลกอริทึมที่ใช้เทคนิคนี้ เช่น อัลกอริทึมคอนเวกซ์ฮัลล์ของ Timothy M. Chan

ตัวอย่างการสร้างคอนเวกซ์ฮัลล์ของ Chan – สร้างภาพโดยอาศัยโค้ดต้นฉบับจาก Wikipedia