เลขฟีโบนัชชีและการพิสูจน์อุปนัยแบบพร้อมเพรียงกัน

Thursday, August 23, 2018, 08:11 AM

ลำดับฟีโบนัชชีนั้น แม้จะนิยามขึ้นมาจากความสัมพันธ์เวียนเกิดง่ายๆ $F_{n} = F_{n - 1} + F_{n - 2}$ และจุดเริ่มต้นที่ $F_{1} = F_{2} = 1$ แต่ก็ทำให้เกิดเอกลักษณ์อันสวยงามต่างๆ มากมาย เช่น $\sum_{i = 1}^{n} F_{i} = F_{n + 2} - 1$ การพิสูจน์เอกลักษณ์เหล่านี้สามารถทำได้โดยง่ายผ่านการอุปนัยเชิงคณิตศาสตร์

แต่ก็ยังมีเอกลักษณ์บางอย่างที่ดูแล้วไม่น่าเป็นไปได้ที่จะพิสูจน์ด้วยเทคนิคข้างต้น เช่น

F_{n}^{2} + F_{n - 1}^{2} = F_{2 n - 1}

หรือเอกลักษณ์ที่คล้ายๆ กันอย่าง

F_{n + 1} F_{n} + F_{n} F_{n - 1} = F_{2 n}

ถึงแม้เราสามารถสังเกตจากการทดลองได้ว่า สมการข้างต้นเป็นจริงเมื่อ $n$ มีค่าน้อยๆ ก็ตามที แต่หากยังไม่ได้พิสูจน์ เราจะแน่ใจได้อย่างไรว่าสมการข้างต้นจะเป็นจริงสำหรับ $n$ ใดๆ?

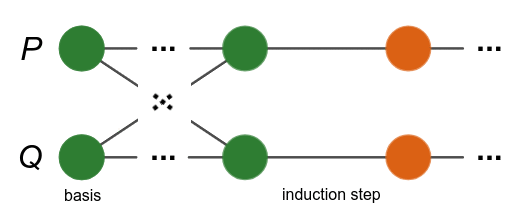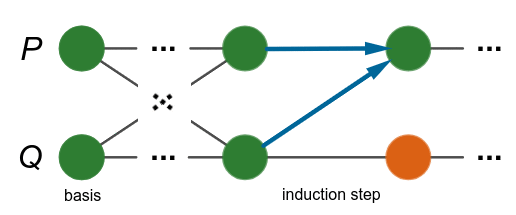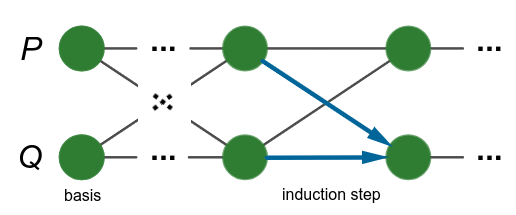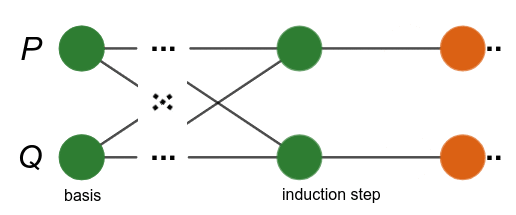
เทคนิคที่จะนำมาใช้พิสูจน์สมการข้างต้น ทำได้โดยการขยายขีดความสามารถของการอุปนัยขึ้นไป กล่าวคือแทนที่เราจะพิสูจน์ให้เห็นว่าเป็นจริงทีละสมการ ก็เปลี่ยนมาพิสูจน์ทั้งสองสมการพร้อมกันไปเลย ซึ่งทำได้ดังนี้

ก่อนอื่น ให้ $P (n)$ แทนค่าความจริงของสมการ $F_{n}^{2} + F_{n - 1}^{2} = F_{2 n - 1}$ และในทำนองเดียวกัน ให้ $Q (n)$ แทนค่าความจริงของสมการ $F_{n + 1} F_{n} + F_{n} F_{n - 1} = F_{2 n}$

สังเกตได้ไม่ยากว่า $P (2)$ และ $Q (2)$ เป็นจริง

ขั้นต่อไป สมมติให้ $P (k)$ และ $Q (k)$ เป็นจริง สิ่งที่เราต้องการคือแสดงให้เห็นว่า $P (k + 1)$ และ $Q (k + 1)$ เป็นจริงด้วย

เริ่มจากฝั่ง $P (k + 1)$ ก่อน จะเห็นว่า

\begin{aligned} F_{k + 1}^{2} + F_{k}^{2} & = (F_{k} + F_{k - 1})^{2} + F_{k}^{2} \\ = (F_{k}^{2} + 2 F_{k} F_{k - 1} + F_{k - 1}^{2}) + F_{k}^{2} \\ = (F_{k}^{2} + F_{k - 1}^{2}) + 2 F_{k} F_{k - 1} + F_{k}^{2} \\ = (F_{k}^{2} + F_{k - 1}^{2}) + F_{k} F_{k - 1} + F_{k} F_{k - 1} + F_{k}^{2} \\ = (F_{k}^{2} + F_{k - 1}^{2}) + F_{k} F_{k - 1} + F_{k} (F_{k - 1} + F_{k}) \\ = \underset{induction}{\underset{⏟}{(F_{k}^{2} + F_{k - 1}^{2})}} + \underset{mutual equation}{\underset{⏟}{F_{k} F_{k - 1} + F_{k} F_{k + 1}}} \\ = F_{2 k - 1} + F_{2 k} \\ = F_{2 k + 1} \end{aligned}

และแน่นอนว่าฝั่ง $Q (k + 1)$ ก็สามารถถูกพิสูจน์ได้ในทำนองเดียวกัน

\begin{aligned} F_{k + 2} F_{k + 1} + F_{k + 1} F_{k} & = (F_{k + 1} + F_{k}) F_{k + 1} + (F_{k} + F_{k - 1}) F_{k} \\ = (F_{k + 1}^{2} + F_{k} F_{k + 1}) + (F_{k}^{2} + F_{k - 1} F_{k}) \\ = \underset{mutual equation}{\underset{⏟}{(F_{k + 1}^{2} + F_{k}^{2})}} + \underset{induction}{\underset{⏟}{(F_{k} F_{k + 1} + F_{k - 1} F_{k})}} \\ = F_{2 k + 1} + F_{2 k} \\ = F_{2 k + 2} \end{aligned}

เราอาจเรียกเทคนิคนี้ว่าเป็นการพิสูจน์โดยอุปนัยแบบพร้อมเพรียงกัน (simultaneous induction)

แผนภาพแนวคิดการพิสูจน์โดยอุปนัยแบบพร้อมเพรียงกัน

ความเจ๋งของเอกลักษณ์ทั้ง 2 สมการข้างต้นนี้ คือมันช่วยให้เราได้อัลกอริทึมคำนวณค่าฟีโบนัชชีที่ตำแหน่ง $n$ ภายในเวลา $O (\log n)$ ซึ่งสังเกตได้จากการที่ฝั่งขวาของทั้งสองสมการนั้น ตำแหน่งฟีโบนัชชีจะมีค่าเป็นสองเท่าของตำแหน่งฟีโบนัชชีทางซ้ายมือของสมการ ทำให้เราสามารถกระโดดข้ามการคำนวณค่าฟีโบนัชชีในตำแหน่งที่ไม่จำเป็นได้เป็นจำนวนมาก

ส่วนการนำไปใช้งานจริงนั้น เราอาจจัดรูปเอกลักษณ์ในกรณีเลขคู่ให้กลายเป็น $F_{n} (2 F_{n + 1} - F_{n}) = F_{2 n}$ เสียก่อน เพื่อลดจำนวนพจน์ฟีโบนัชชีที่แตกต่างกันลง (จากเดิมต้องรู้ทั้ง $F_{n - 1}, F_{n}, F_{n + 1}$ ) อัลกอริทึมที่คำนวณค่าฟีโบนัชชีด้วยวิธีนี้มีชื่อว่า fast doubling ซึ่งสามารถเขียนเป็นโค้ดได้ดังนี้

def fibonacci(n):
    if n in {1, 2}:
        return 1
    elif n % 2 == 0:
        f0 = fibonacci(n//2)
        f1 = fibonacci(n//2+1)
        return f0 * (2*f1 - f0)
    else:
        f0 = fibonacci(n//2 + 1)
        f1 = fibonacci(n//2)
        return f0**2 + f1**2

หมายเหตุ

บล็อกตอนนี้อาจถือได้ว่าเป็นตอนต่อของการคำนวณค่าฟิโบนัชชีด้วยเมทริกซ์ ซึ่งเราสามารถมาถึงข้อสรุปของเอกลักษณ์ข้างต้นได้เช่นกัน ผ่านการแก้สมการเมทริกซ์จากตอนที่แล้วต่อดังนี้

\begin{aligned} {[\begin{array}{c} 1 & 1 \\ 1 & 0 \end{array}]}^{2 n} & = {[\begin{array}{c} 1 & 1 \\ 1 & 0 \end{array}]}^{n} {[\begin{array}{c} 1 & 1 \\ 1 & 0 \end{array}]}^{n} \\ = [\begin{array}{c} F_{n + 1} & F_{n} \\ F_{n} & F_{n - 1} \end{array}] [\begin{array}{c} F_{n + 1} & F_{n} \\ F_{n} & F_{n - 1} \end{array}] \\ [\begin{array}{c} F_{2 n + 1} & F_{2 n} \\ F_{2 n} & F_{2 n - 1} \end{array}] & = [\begin{array}{c} F_{n + 1}^{2} + F_{n}^{2} & F_{n + 1} F_{n} + F_{n} F_{n - 1} \\ F_{n} F_{n + 1} + F_{n - 1} F_{n} & F_{n}^{2} + F_{n - 1}^{2} \end{array}] \end{aligned}

อ้างอิง

Lovász, L., Pelikán, J. and Vesztergombi, K., 2003. Discrete mathematics, Undergraduate Texts in Mathematics.

neizod

author

« เป็นทุกอย่าง

ค้นหาผลลัพธ์อย่างรวดเร็ว เมื่อเริ่มด้วยอัลกอริทึมที่กำหนดขนาดคำตอบ »

neizod's speculation

insufficient data for meaningful answer

เลขฟีโบนัชชีและการพิสูจน์อุปนัยแบบพร้อมเพรียงกัน

หมายเหตุ

อ้างอิง