TechJam 2018 รอบชิงภาคกลาง
เนื่องจาก TechJam ไม่ได้เปิดเผยรายชื่อผู้เข้ารอบเป็นข้อมูลสาธารณะ พอถึงหน้างานเลยเพิ่งรู้ว่านี่มันงานรวมญาติสสวท.คอมพิวเตอร์โอลิมปิกนี่หน่า! รู้สึกว่ามาผิดงานซะเหลือเกิน 5555 มองไปทางไหนก็เจอแต่คนใส่เสื้อ Google Code Jam เต็มไปหมด (ส่วนเรานี่สาย Open Source เลยใส่เสื้อ Hacktoberfest ไป) เดินไปเดินมาซักพักก็เจอ @haxxpop กับ @dtinth ก็เลยจับกลุ่มร่วมกับ @ipats เพื่อนร่วมทีม (ผู้มาสาย) นั่งคุยสัพเพเหระกันระหว่างรอแข่งขัน
กติการการแข่งขัน TechJam รอบนี้มีโครงสร้างเหมือนรอบคัดเลือกเลย คือ แบ่งคำถามออกเป็นข้อเล็กและใหญ่ บางช่วงมีลักษณะออกแนววาไรตี้เกมโชว์ที่ต้องชิงกันตอบ ไม่ได้กะให้นั่งซีเรียสยาวๆ หลายชั่วโมงเพื่อเขียนอัลกอริทึมโหดๆ แก้ปัญหาเหมือนพวก ACM-ICPC, Google Code Jam เพียงอย่างเดียว ก็ถือว่าหลากหลายแปลกใหม่สร้างสรรค์ดี เป็นอีกทางเลือกที่ดูตื่นเต้นสนุกสนานไม่แพ้การแข่งกินเบียร์ระหว่างโค้ดที่เคยไปร่วมเมื่อหลายปีก่อนเลย 🍻
ย้ำอีกครั้งว่าวิธีคิดและโค้ดที่เอามาแปะนี่คือแบบที่ทำความสะอาดเรียบร้อยแล้ว ตอนแข่งจริงโดนเวลาบีบค้นจนโค้ดเละกว่านี้มาก!
ข้อเล็กๆ ถามสั้นตอบไว
ตอนรอบคัดเลือกไม่ได้สนใจรายละเอียดตรงนี้นัก แต่จริงๆ แล้วรอบนี้แบ่งยังแยกย่อยลงไปอีกสองแบบ คือ แบบที่ให้ไวท์บอร์ดเล็กๆ มาเขียนตอบด้วยสัญชาติญาณ (30 วินาที) กับให้ใช้คอมพิวเตอร์เขียนโปรแกรมอย่างเร็วเพื่อหาคำตอบ (5 นาที) … พอมีเวลามาบังคับแล้วยอมรับเลยว่าลนมากๆ ยิ่งข้อที่ให้เขียนโปรแกรมนี่ถ้าได้เวลาเพิ่มขึ้นมาอีกซักสิบวินาทีก็น่าจะได้คำตอบแล้ว
ลึกและกว้าง
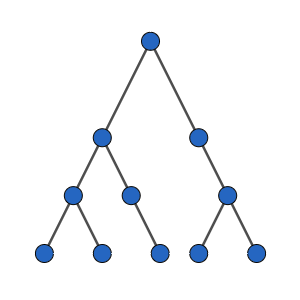
โจทย์ให้พรีออเดอร์ (NLR) จากการทำ DFS บนต้นไม้ค้นหาแบบทวิภาคมา แล้วถามว่าการท่องต้นไม้แบบ BFS สามารถทำได้แตกต่างกันทั้งหมดกี่แบบ
จำเลขโหนดเป๊ะๆ ไม่ได้ แต่เห็นโจทย์แล้วพยายามเขียนสร้างต้นไม้ไปด้วย (รู้สึกจะสร้างผิดเงื่อนไขการเป็นต้นไม้ค้นหาซะอีก แต่รูปดันออกมาใช้ได้พอดี) ซึ่งได้ผลลัพธ์หน้าตาประมาณนี้
ตัวอย่างต้นไม้ค้นหาแบบทวิภาค ที่มีโหนดที่มีลูกสองตัวอยู่ 4 โหนด
ผมนับรอบแรกแล้วผิด จนได้ @ipats มาสะกิดวินาทีสุดท้ายว่ามันต้องคูณ 2 เข้าไปทุกโหนดที่มีลูกสองตัวนะ ไม่ใช่แค่ที่โหนดที่มีสองใบ ดังนั้นตอบ 16 แบบ
นับพื้นที่สามเหลี่ยม
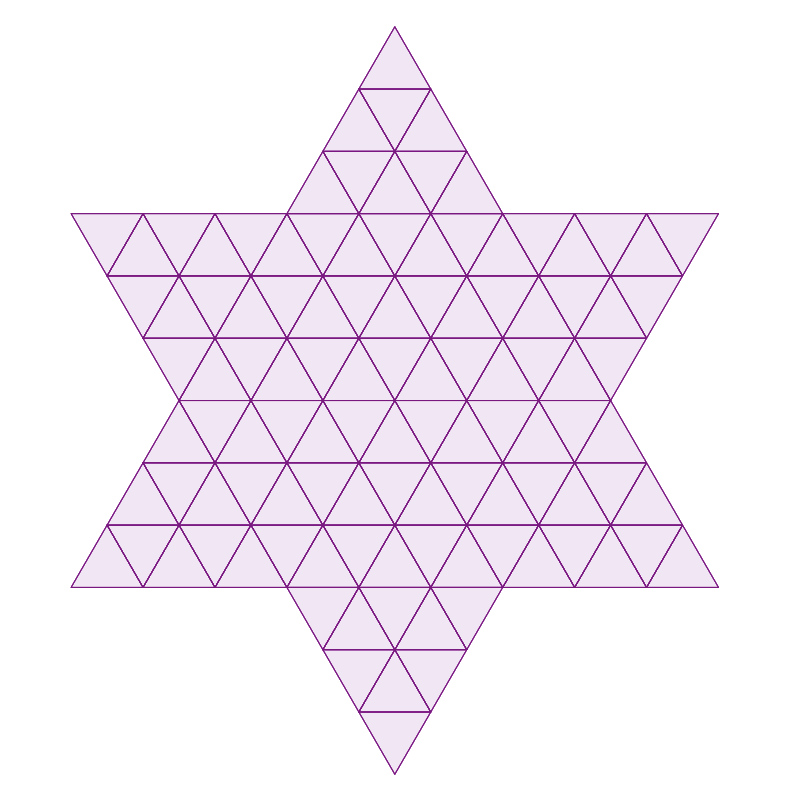
โจทย์ให้รูปนี้มาแล้วถามว่าถ้าสร้างวงจรออยเลอร์ (ลากเส้นตรงผ่านทุกจุดโดยไม่ซ้ำจุดเดิม และวนรอบกลับมาที่จุดแรกได้พอดี) จะสร้างพื้นที่จากรูปสามเหลี่ยมย่อยๆ ได้ขนาดใหญ่ที่สุดเท่าไหร่?
มาวาดรูปทีหลังแล้วลืมใส่จุด … จินตนาการเอาว่าที่ทุกๆ มุมสามเหลี่ยมเล็กมันมีจุดอยู่ละกันนะ 😅
ให้ทดลองลากเส้นแล้วยืนนับคงตอบไม่ทันใน 30 วินาที … กรรมการเฉลยว่าข้อนี้ต้องมองให้ออกว่าพื้นที่ที่มากที่สุดสร้างได้ สามารถคำนวณได้จากจำนวนจุดลบด้วย 2 (พอมองออกแล้วพิสูจน์อุปนัยจะง่ายมาก)
วิธีนับจุดเร็วๆ ก็ขอไอเดียได้จากเกาส์ ซึ่งจะได้ว่าจุดทั้งหมดมี $T_{10}+3T_3 = 73$ จุด ดังนั้นจึงได้พื้นที่เป็น 71 สามเหลี่ยมเล็ก
ครอบครัวนักคำนวณ
ให้ครอบครัวนักคำนวณซึ่งประกอบไปด้วย Hilbert, Shannon, Dijkstra, Lovelace, Neumann และมีความสัมพันธ์ดังนี้
- Hilbert อายุน้อยกว่า Shannon
- Dijkstra อายุน้อยกว่า Lovelace
- Shannon อายุน้อยกว่า Neumann
- Hilbert อายุน้อยกว่า Dijkstra
- Lovelace อายุน้อยกว่า Shannon
- Shannon อายุน้อยกว่า Dijkstra
- Neumann อายุน้อยกว่า Lovelace
ถามว่าในความสัมพันธ์นี้มีข้อใด (เพียงข้อเดียว) ที่ผิด? และเมื่อลบความสัมพันธ์ที่ผิดนั้นออกแล้ว ใครจะมีอายุมากที่สุด?
ข้อนี้ @ipats ตอบได้อย่างรวดเร็ว เพียงแค่เอาความสัมพันธ์ข้างต้นมาเขียนเป็นกราฟแล้วจะเห็นว่ามีความสัมพันธ์ L<S ที่ทำให้กราฟมีวงจร พอตัดเส้นนี้ทิ้งเพียงเส้นเดียวแล้วกราฟก็จะกลายเป็นต้นไม้ทันที และได้ว่าครอบครัวนี้มี Lovelace เป็นพี่ใหญ่
#adalovelaceday #ALD18 Mathematician, writer, worked on Babbage's Analytical Engine, recognised computing could be used for more than calculation and wrote the first algorithm #womeninSTEM pic.twitter.com/mHON10PBpd
— Science and Industry Museum (@sim_manchester) October 9, 2018
จัดกลุ่มตัวเลขที่ผลคูณต่างกันน้อยสุด
โจทย์ให้เซ็ต $A=\lbrace1,2,3,\dots,12\rbrace$ มา ถามว่าการแบ่งพาร์ทิชันเซ็ตนี้เป็นสองเซตย่อย แล้วผลต่างของผลคูณของแต่ละเซ็ตย่อยที่มีค่าน้อยสุดเป็นเท่าไหร่?
ขอบคุณ Python ที่มี itertools.combinations เลยเขียนข้อนี้ทันอย่างฉิวเฉียด
from itertools import combinations
from functools import reduce
from operator import mul
prod = lambda ls: reduce(mul, ls)
ls = set(range(1, 13))
ans = set()
for i in range(1, 12):
for rs in combinations(ls, i):
rs = set(rs)
ans |= {abs(prod(rs) - prod(ls-rs))}
print(min(ans))
รันโปรแกรมแล้วตอบว่าผลต่างที่น้อยที่สุดคือ 576
ยกกำลังด้วยการคูณน้อยที่สุด
โจทย์ถามว่า $x^{125}$ สามารถเขียนด้วยผลคูณที่สร้างจากการคูณกันของพจน์ที่อยู่ในฟอร์ม $x^k$ ที่แตกต่างกันอย่างน้อยที่สุดกี่พจน์?
ข้อนี้จะเขียนโปรแกรมคิดแบบการยกกำลังด้วยกำลังสองก็ได้ … ซึ่งจะผิด ส่วน @ipats ทำด้วยมือด้วยการสร้าง $x^2, x^4, x^8,\dots$ ไปเรื่อยๆ จนได้คำตอบว่า 11 … ซึ่งก็ผิดอีกเช่นกัน เพราะจริงๆ แล้วข้อนี้จะออกแนวปัญหาเชาวน์ที่ต้องมองให้ออกว่าการสร้างเลขที่เป็น $x^{5k}$ สามารถใช้พจน์อย่างประหยัดที่สุดคือ $x^{2k} \cdot x^{2k} \cdot x^k$ ดังนั้นคำตอบจะกลายเป็น
\[\begin{align*} x \cdot x &= x^2 \\ x \cdot x^2 &= x^3 \\ x^2 \cdot x^3 &= x^5 \\ x^5 \cdot x^5 &= x^{10} \\ x^5 \cdot x^{10} &= x^{15} \\ x^{10} \cdot x^{15} &= x^{25} \\ x^{25} \cdot x^{25} &= x^{50} \\ x^{25} \cdot x^{50} &= x^{75} \\ x^{50} \cdot x^{75} &= x^{125} \end{align*}\]คือทำได้ใน 9 ครั้ง (โดนโจทย์ดักจนตอบผิดกันหมดทุกทีม 555)
นับรูปแบบพิซซ่า
ให้พิซซ่าหนึ่งถาดตัดแบ่งเป็นได้ 8 ชิ้น แต่ละชิ้นสามารถเลือกซอสได้ 3 แบบ ถามว่าสร้างพิซซ่าที่แตกต่างกันได้ทั้งหมดกี่แบบ? โดยให้คำนึงด้วยว่าพิซซ่าที่หมุนแล้วเหมือนกัน จะถูกนับว่าเป็นแบบเดียวกัน
ข้อนี้ตอนทำจริงเขียนไม่ทันเพราะอ่อนซ้อมจนลืมไปว่ามี itertools.product ให้ใช้ (ไม่ได้ใช้บ่อยเท่าตัว combinations) เลยมัวแต่บั๊กที่เขียนฟังก์ชันนี้เอง … พอแข่งเสร็จกลับมาตั้งสติแล้วเขียนดีๆ ก็เหลือแค่นี้
from itertools import product as cartesian_product
rotate = lambda pizza, i: pizza[i:] + pizza[:i]
minimum = lambda pizza: min(sorted(rotate(pizza, i) for i in range(8)))
print(len({minimum(pizza) for pizza in cartesian_product('012', repeat=8)}))
รันโปรแกรมแล้วตอบ 834 แบบ
ข้อใหญ่ๆ แก้โจทย์สนใจ Big-O
โจทย์ทำแบบเดียวกับ Google Code Jam คือมีเทสเคสทั้งแบบง่าย (เขียนถึกๆ ไปก็น่าจะออก) และแบบยาก (ต้องใช้อัลกอริทึมที่เหมาะสม) … ซึ่งเละครับ ไม่ได้ซ้อมมา มีโจทย์ 3 ข้อทำได้แค่เทสเคสง่าย 2 ข้อเท่านั้น ก็ขอจดเฉลยแค่แบบง่าย (ที่ทำทันตอนแข่ง) ละกัน ส่วนเฉลยเทสเคสยากนั้นน่าจะมีคนอยากอธิบายอยู่แล้วนะ ไปฟังจากคนที่เก่งกว่าเราตรงๆ เลยดีกว่า 😉
สลับสายโพลิเมอร์
ให้โพลิเมอร์ $K$ ซึ่งเป็นสตริงที่มีความยาว $N$ โดยนับตำแหน่งเริ่มต้นที่เลขศูนย์ และให้ข้อมูลตำแหน่ง $p$ ที่ต้องการทำงานมาอีก $M$ ครั้ง โดยแต่ละครั้งที่ทำงาน จะกลับซับสตริงฝั่งซ้ายของ $K_p$ และกลับซับสตริงฝั่งขวาของ $K_p$ ดังตัวอย่างต่อไปนี้
Input Polymer: ASDFGHJKL
p = 3 ^
Intermediate: DSAFLKJHG
p = 6 ^
Intermediate: KLFASDJGH
p = 0 ^
Final Output: KHGJDSAFL
ให้เขียนโปรแกรมที่ตอบผลลัพธ์ของการทำงานสลับสตริงดังกล่าว โดยเทสเคสง่าย $1 \le N \le 300$ และ $0 \le M \le 30\text{k}$ ส่วนเทสเคสยาก $1 \le N \le 300\text{k}$ และ $0 \le M \le 300\text{k}$
ซึ่งโค้ดที่พอจะผ่านเทสเคสง่ายก็เขียนเพียงเท่านี้
n, m = [int(n) for n in input().split()]
polymer = list(input().strip())
for _ in range(m):
p = int(input())
polymer = polymer[:p][::-1] + polymer[p:p+1] + polymer[p+1:][::-1]
print(''.join(polymer))
จะเห็นว่ามันเสียเวลาหนักๆ ตรงที่ต้องสร้างสตริงใหม่ทุกครั้ง … ซึ่งตอนแข่งก็พอจะนึกถึงโครงสร้างข้อมูลที่แก้ปัญหาตรงนี้ได้แล้ว แต่เขียนไม่ทันอยู่ดี 555
แต่ความทึ่งที่สุดคือเมื่อแข่งเสร็จแล้วเดินออกมาคุยกับทีมอื่นๆ ก็พบว่ามีเฉลยที่เรียบง่ายเพียงแค่นี้
n, m = [int(i) for i in input().split()]
j = n
flipped = False
polymer = list(input().strip()) + ['_']
for _ in range(m):
r = int(input())
i = (j+r+1 if not flipped else j-r-1) % (n+1)
polymer[i], polymer[j] = polymer[j], polymer[i]
j = i
flipped = not flipped
if not flipped:
print(''.join(polymer[j+1::+1]+polymer[:j:+1]))
else:
print(''.join(polymer[j-1::-1]+polymer[:j:-1]))
เอิ่ม … เหมือนโดนคนแต่งโจทย์ดักเข้าให้อีกแล้วแฮะ 😅
ลดค่าผ่านทางหลวง
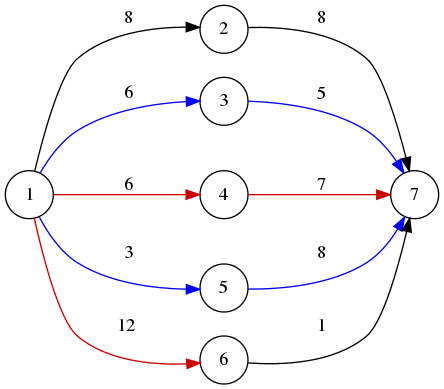
ให้กราฟมีทิศทางที่แต่ละโหนดแทนเมืองและเส้นเชื่อมแทนทางหลวงที่มีการเก็บค่าผ่านทาง ซึ่งปัจจุบันมีเส้นทางที่ถูกที่สุดที่เป็นทางผ่านจากเมือง $1 \to N$ อยู่แล้ว อยากสร้างเส้นทางถูกที่สุดอีกอย่างน้อยหนึ่งเส้นทาง ซึ่งทำได้โดยลดค่าผ่านทางหลวงได้หนึ่งเส้น โดยการลดค่าผ่านทางนี้ต้องไม่กระทบกับเส้นทางที่ถูกที่สุดที่มีอยู่ และไม่สามารถลดค่าผ่านทางจนติดลบได้ ถามว่าต้องลดค่าผ่านทางอย่างน้อยสุดเป็นเงินเท่าไหร่?
ตัวอย่างกราฟทางหลวง โดยเส้นสีฟ้าแสดงเส้นทางที่ถูกที่สุด (มีอยู่แล้ว 2 เส้นทาง เส้นทางละ 11 หน่วย) ส่วนเส้นสีแดงคือสามารถลดราคาค่าผ่านทางเส้นใดเส้นหนึ่งก็ได้ในราคา 2 หน่วย เพื่อสร้างเส้นทางที่ถูกที่สุดเพิ่ม
ข้อจำกัดของเทสเคสง่ายคือ $3 \le N \le 50$ และ $1 \le M \le 2\text{k}$ ส่วนเทสเคสยากนั้น $3 \le N \le 100\text{k}$ และ $1 \le M \le 200\text{k}$
ข้อนี้ @ipats น่าจะคิดเกือบออกแล้ว เสียดายที่เราไม่ถนัดอัลกอริทึมบนกราฟ แค่จะเขียนโค้ดมาทดลองตามยังทำไม่ได้เลย 😭 (ส่วน @ipats ดันก็ถนัดแต่ PHP ซึ่งการแข่งขันนี้เป็นแบบส่งโค้ดและไม่รองรับ ถถถ)
แข่งเสร็จมาคุยกับทีมอื่นๆ ก็ได้แนวคิดสำหรับแก้โจทย์ว่า เริ่มจากหาเส้นทางที่สั้นที่สุด จาก $1 \to N$ เก็บเป็น prefix แล้วสลับทิศทางของกราฟมาหาเส้นทางที่สั้นที่สุดจาก $N \to 1$ เก็บเป็น postfix หลังจากนั้นพิจารณาทางหลวงที่เชื่อมเมือง $u \to v$ ใดๆ คำนวณค่าผ่านทางจาก $1 \to u \to v \to N$ (ซึ่งทำได้เร็วโดยดูจากค่าใน prefix และ postfix บวกกันได้เลย) แล้วทดลองลดค่าผ่านทาง $u \to v$ ว่าจะสามารถทำให้ค่าผ่านทางรวมเท่ากับค่าผ่านทางที่ถูกที่สุดได้มั้ย ทำไปเรื่อยๆ ให้ครบทุกเส้นทางเพื่อหาการลดค่าผ่านทางที่ถูกที่สุด
หรือนำไอเดียข้างต้นมาเขียนโค้ดคร่าวๆ ก็น่าจะได้ประมาณนี้
from collections import defaultdict
from heapq import heappush, heappop
def dijkstra(graph, root):
dist = {u: 0 if u == root else 1e400 for u in graph}
queue = [(dist[root], root)]
while queue:
best, u = heappop(queue)
for v, cost in graph[u].items():
dist[v] = min(dist[v], best+cost)
heappush(queue, (dist[v], v))
return dist
def exceed_shortest(n, graph, prefix, postfix, avoid=set()):
best = prefix[n]
exceed = defaultdict(set)
for u, edges in graph.items():
for v, cost in edges.items():
if (u, v) not in avoid:
value = prefix[u] + postfix[v] + cost - best
if value < cost:
exceed[value] |= {(u, v)}
return exceed
def solve(n, direct, invert):
prefix, postfix = dijkstra(direct, 1), dijkstra(invert, n)
exceed = exceed_shortest(n, direct, prefix, postfix)
exceed = exceed_shortest(n, direct, prefix, postfix, exceed[0])
return min(exceed) if exceed else 0
def main():
n, m = [int(n) for n in input().split()]
direct = {u: {} for u in range(1, n+1)}
invert = {v: {} for v in range(1, n+1)}
for _ in range(m):
u, v, c = [int(n) for n in input().split()]
direct[u][v] = invert[v][u] = c
print(solve(n, direct, invert))
if __name__ == '__main__':
main()
ขุดสมบัติ
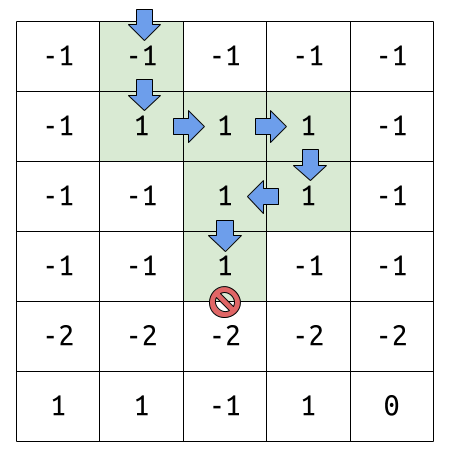
มีลายแทงสมบัติในแนวดิ่งเป็นตารางขนาด $R \times C$ โดยแต่ละช่องอาจมีสมบัติที่มีราคาติดลบได้ เราต้องการขุดสมบัติลึกลงไปเรื่อยๆ ให้ได้มูลค่ารวมมากที่สุด โดยในขณะที่ขุดไปจนถึงความลึกหนึ่งๆ เราอาจเลือกได้ว่าจะเลี้ยวซ้ายหรือขวาหนึ่งครั้งไปไกลสุด $K$ ช่องแล้วขุดลงชั้นถัดไป (หรือจะหยุดขุดก็ได้) แต่เครื่องขุดสมบัติจะขุดถอยหลังหรือขุดย้อนขึ้นด้านบนไม่ได้ ถามว่าเราสามารถขุดหาสมบัติได้มากที่สุดเป็นมูลค่าเท่าไหร่?
ตัวอย่างแผนที่สมบัติ และการขุดที่ให้มูลค่ามากที่สุดที่ 5 หน่วย
เทสเคสง่ายน่าจะให้ $1 \le R, C \le 200$ และเทสเคสยาก $1 \le R \times C \le 2\text{M}$ โดยทั้งสองเคส $K \le C$
มองผ่านๆ รอบแรก ข้อนี้เป็นปัญหาที่ใช้เทคนิคกำหนดการพลวัตธรรมดาๆ ไล่หาย้อนขึ้นไปว่า จากช่องนี้เมื่อขุดต่อลงไปเรื่อยๆ จะทำได้ดีที่สุดเท่าไหร่ ก็จะได้โค้ดนี้ที่ผ่านเทสเคสง่าย
def sign(n):
return +1 if n > 0 else -1 if n < 0 else 0
def possible(layer, i, kp, below):
out = {0}
acc = 0
for j in range(0, kp, sign(kp)):
if not 0 <= i+j < len(layer):
break
acc += layer[i+j]
out |= {acc + below[i+j]}
return out
def max_cell(layer, i, k, below):
left = possible(layer, i, -k-1, below)
right = possible(layer, i, k+1, below)
return max(left | right)
def solve(grid, r, c, k):
best = [0 for _ in range(c)]
while grid:
layer = grid.pop()
best = [max_cell(layer, i, k, best) for i in range(c)]
return max(best)
def main():
r, c, k = [int(n) for n in input().split()]
grid = [[int(n) for n in input().split()] for _ in range(r)]
print(solve(grid, r, c, k))
if __name__ == '__main__':
main()
แต่ความโหดคือการที่โจทย์ยอมให้หัวเจาะเลี้ยวได้ไกลถึง $K \le C$ นั่นหมายความว่าอัลกอริทึมข้างต้นที่กินเวลา $O(RC^2)$ จะทำงานเทสเคสยากไม่ทันนั่นเอง (ยอม คิดไม่ออกแล้ว)
สรุป
การแข่งขันสนุกมากครับ แม้ผมเองจะแก้โจทย์ไม่ค่อยได้ ตกเป็นไปเป็นอันดับท้ายๆ ก็ตามที แต่ก็ได้เห็นถึงฝีมือขั้นปีศาจของทีมอื่นๆ ที่สำคัญคือมีหลายทีมทีเดียวที่ยังเป็นเด็กม.ปลาย! ได้เห็นแล้วรู้สึกว่าวงการไอทีของไทยยังมีความหวังอยู่นะ เชื่อว่างานนี้น่าจะเป็นตัวจุดประกายความสนใจและความเข้าใจต่อแวดวงไอที (และ STEM) ให้สังคมเราได้เป็นอย่างดี

author