ลองจินตนาการว่าเรากำลังจะเปิดบริษัทแต่ยังขาดพนักงานเลขา ซึ่งตำแหน่งดังกล่าวถือว่าเป็นตำแหน่งฮอตฮิตที่บริษัทไหนๆ ก็ต่างแย่งชิงตัว การเรียกผู้สมัครมาสัมภาษณ์งานจึงจำเป็นต้องตอบรับทันทีเดี๋ยวนั้น มิเช่นนั้นแล้วก็รับประกันได้เลยว่าผู้สมัครจะถูกบริษัทอื่นแย่งตัวไปในทันทีที่เขาก้าวเท้าออกจากออฟฟิศ

สมมติว่าเราสามารถเรียกผู้สมัครมาสัมภาษณ์ได้มากที่สุด $n$ คน โดยถือว่าก่อนสัมภาษณ์เราไม่รู้อะไรเกี่ยวกับผู้สมัครเลย และเมื่อสัมภาษณ์เสร็จเราก็จะบอกได้แค่ว่าผู้สมัครคนนี้ดีกว่าหรือแย่กว่าผู้สมัครคนก่อนๆ ที่เคยสัมภาษณ์ เราจะมีเทคนิคอย่างไรในการเฟ้นหาผู้สมัครเพียงหนึ่งคนที่ดีที่สุด?

มองเผินๆ นี่อาจจะดูเหมือนปัญหาที่ไม่น่าเป็นไปได้ ในเมื่อเราไม่รู้ว่าใครดีกว่าใครจนกว่าจะได้สัมภาษณ์ แต่พอสัมภาษณ์เสร็จก็ต้องตอบรับว่าจะให้ร่วมทางกับบริษัทเราหรือไม่ซะแล้ว หากเราถอดใจไม่วางแผนใดๆ และเลือกตอบรับผู้สมัครแบบสุ่ม โอกาสที่จะได้ผู้สมัครที่ดีที่สุดก็จะมีเพียงแค่ $1/n$ เท่านั้น

แต่เนื่องจากเราสามารถเปรียบเทียบผู้สมัครได้ หากเราลองสัมภาษณ์ผู้สมัครคนแรกดูก่อน (และต้องแข็งใจบอกปฏิเสธไป) เพื่อเป็นบรรทัดฐานว่าเราอยากได้ผู้สมัครประมาณไหน เมื่อสัมภาษณ์ต่อไปและพบว่าผู้สมัครคนที่สองดีกว่าคนแรก อย่างน้อยโอกาสที่เขาจะเป็นผู้สมัครที่ดีที่สุดก็มีมากกว่าการสุ่มแน่ๆ

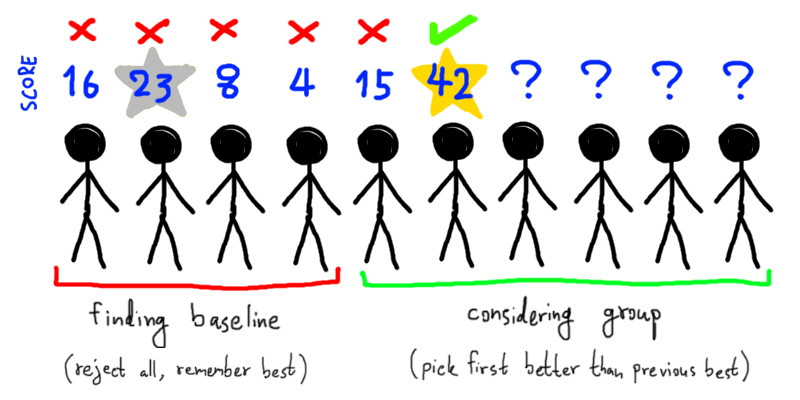
หากเราแบ่งการสัมภาษณ์ออกเป็น 2 ช่วง โดยช่วงแรกสัมภาษณ์ผู้สมัครเป็นสัดส่วน $0<r\le 1$ ต่อผู้สมัครทั้งหมด เพื่อหาบรรทัดฐานของผู้สมัครที่เราต้องการ แล้วในช่วงหลังจึงสัมภาษณ์ผู้สมัครที่เหลือ เมื่อใดที่เจอผู้สมัครที่ดีกว่าทุกคนที่เคยเจอมา เราจะตอบรับให้ผู้สมัครคนนี้มาร่วมงานทันที โอกาสที่ผู้สมัครคนนี้จะเป็นผู้สมัครที่ดีที่สุดก็คือ

\[P(\text{pick $1^{st}$}) = \sum_{k=1}^n P(\text{baseline is $k^{th}$}) \cdot P(\text{saw $k^{th}$ pick $1^{st}$}) \\\]

โดยที่

• $1^{st}$ คือผู้สมัครที่ดีที่สุด (อันดับหนึ่ง) $n^{th}$ คือผู้สมัครที่แย่ที่สุด และไม่มีใครอยู่อันดับเดียวกัน
• $\text{pick $1^{st}$}$ แทนเหตุการณ์ที่ได้ผู้สมัครที่ดีที่สุดจากกระบวนการทั้งหมด
• $\text{baseline is $k^{th}$}$ แทนเหตุการณ์ที่ผู้สมัครอันดับที่ $k^{th}$ เป็นบรรทัดฐานในการสัมภาษณ์ช่วงแรก
• $\text{saw $k^{th}$ pick $1^{st}$}$ แทนเหตุการณ์ที่ใช้ $k^{th}$ เป็นฐานแล้วได้ผู้สมัครที่ดีที่สุดในการสัมภาษณ์ช่วงหลัง

ซึ่งเราจะเห็นว่า

• $\text{saw $1^{th}$ pick $1^{st}$}$ เป็นไปไม่ได้
• $\text{baseline is $k^{th}$}$ หมายความว่า ในการสัมภาษณ์ช่วงแรก นอกจากจะเห็นผู้สมัครอันดับที่ $k^{th}$ แล้ว จะต้องไม่เห็นผู้สมัครตั้งแต่อันดับ $1^{st}$ ถึง $(k-1)^{th}$ ด้วย

หาก $n$ มีขนาดเล็กเราจะต้องคำนวณแตกกรณียิบย่อยมากมาย ดังนั้นจะพิจารณาเฉพาะเมื่อ $n$ มีขนาดใหญ่ ที่เราจะเห็นว่าพจน์หลังๆ มีค่าลดลงอย่างรวดเร็ว ทำให้เราสามารถประมาณด้วยอนุกรมอนันต์ได้ ซึ่งก็คือ

\[\begin{align} P(\text{pick $1^{st}$}) &= \sum_{k=1}^n P(\text{baseline is $k^{th}$}) \cdot P(\text{saw $k^{th}$ pick $1^{st}$}) \\ &\approx r \cdot 0 + r \left( 1 - r \right) \cdot 1 + r \left( 1 - r \right)^2 \cdot \frac12 + r \left( 1 - r \right)^3 \cdot \frac13 + \dots \\ &= r \sum_{k=1}^\infty \frac{\left( 1 - r \right)^k}{k} \end{align}\]

ให้ $x=(1-r)$ ปัญหาย่อยของเราจะแปลงไปเป็นการหาผลลัพธ์ของอนุกรมฮาร์โมนิค ที่แต่ละพจน์มีผลคูณของเลขยกกำลังติดมาด้วย ดังนี้

\[\sum_{k=1}^\infty \frac{x^k}k = x + \frac{x^2}2 + \frac{x^3}3 + \frac{x^4}4 + \dots\]

ซึ่งเราสามารถใช้อนุกรมเทย์เลอร์มาช่วยแก้ได้ โดยเทคนิคคือเลือกใช้ฟังก์ชันที่อนุพันธ์อันดับ $k$ มีพจน์ $(k-1)!$ โผล่เข้ามา เพื่อที่เราจะได้เอาไปตัดกับ $1/k!$ จากการกระจายเทย์เลอร์ จนได้ผลลัพธ์เป็นอนุกรมในรูปฮาร์โมนิคอย่างที่เราต้องการ ซึ่งฟังก์ชันที่มีสมบัติดังกล่าวก็คือฟังก์ชันตระกูล $\log$ นั่นเอง

\[\begin{array}{c|c|c} f(x) & \log x & \log(1-x) \\ \hline f'(x) & \frac1x & -\frac1{1-x} \\ f''(x) & -\frac1{x^2} & -\frac1{(1-x)^2} \\ f^{(3)}(x) & \frac{2!}{x^3} & -\frac{2!}{(1-x)^3} \\ f^{(4)}(x) & -\frac{3!}{x^4} & -\frac{3!}{(1-x)^4} \\ \vdots \\ f^{(k)}(x) & \frac{(-1)^{k+1}(k-1)!}{x^k} & -\frac{(k-1)!}{(1-x)^k} \end{array}\]

เลือกกระจาย $\log (1-x)$ รอบจุด 0 จะได้ว่า

\[\begin{align} \log(1-x) &= \sum_{k=1}^\infty \frac{f^{(k)}(0)}{k!}(x-0)^k \\ &= \sum_{k=1}^\infty - \frac{(k-1)!}{(1-0^k)k!}x^k \\ &= - \sum_{k=1}^\infty \frac{x^k}{k} \end{align}\]

ดังนั้น

\[P(\text{pick $1^{st}$}) \approx - r \log r\]

แล้วใช้เทคนิคอนุพันธ์จากแคลคูลัสเพื่อหาค่า $r$ ที่เหมาะสม

\[\begin{align} 0 &= \frac{d}{dr} (-r) \log r \\ &= (-r) \frac{d}{dr}\log r + \log r \frac{d}{dr}(-r) \\ &= -1 - \log r \\ r &= \frac1e \end{align}\]

ก็จะได้คำตอบว่า สัดส่วนที่เหมาะสมที่สุดที่ควรใช้หาบรรทัดฐานในช่วงแรก คือ $1/e \approx 36.8\%$ นั่นเอง นอกจากนี้เมื่อย้อนกลับไปคำนวณความน่าจะเป็น ก็จะเห็นว่า $P(\text{pick $1^{st}$}) \approx 1/e$ อีกด้วย!

และแนวทางการวิเคราะห์ข้างต้นก็สามารถนำไปใช้หาความน่าจะเป็นที่จะได้ผู้สมัครในอันดับอื่นๆ ได้เช่นกัน ดังตัวอย่างอันดับแรกๆ ดังนี้

\[\begin{align} P(\text{pick $2^{nd}$}) &\approx P(\text{pick $1^{st}$}) - \frac1e \left( 1 - \frac1e \right) &\approx 13.6\% \\ P(\text{pick $3^{rd}$}) &\approx P(\text{pick $2^{nd}$}) - \frac1{2e} \left( 1 - \frac1e \right)^2 &\approx 6.2\% \\ P(\text{pick $4^{th}$}) &\approx P(\text{pick $3^{rd}$}) - \frac1{3e} \left( 1 - \frac1e \right)^3 &\approx 3.1\% \\ P(\text{pick $5^{th}$}) &\approx P(\text{pick $4^{th}$}) - \frac1{4e} \left( 1 - \frac1e \right)^4 &\approx 1.6\% \end{align}\]

จะเห็นว่าด้วยวิธีนี้โอกาสที่จะได้ผู้สมัครที่ดีที่สุดสองอันดับแรกก็กินไปแล้วถึงครึ่งนึง 🤯