Code Jam 2021: ตรวจจับคนโกงข้อสอบ

Wednesday, March 31, 2021, 11:44 AM

Google Code Jam รอบคัดเลือกที่ผ่านมาถือว่าเป็นรอบที่น่าสนใจพอสมควร เพราะข้อที่คะแนนมากสุดนั้นเป็นโจทย์เชิงสถิติและความน่าจะเป็นที่เราไม่จำเป็นต้องตอบถูกต้อง 100% ก็ได้ ซึ่งก็ดูเหมาะเจาะกับโลกของการเขียนโปรแกรมในปัจจุบันที่กำลังเปลี่ยนผ่านไปสู่ยุคแห่งวิทยาศาสตร์ข้อมูล การเรียนรู้ของเครื่องจักร และปัญญาประดิษฐ์กันแล้ว

อันที่จริงโจทย์ข้อนี้แอบทำให้นึกถึงความเป็นส่วนตัวเชิงอนุพันธ์ (differential privacy) สาขาวิชาความรู้ใหม่ที่พยายามรักษาความเป็นส่วนตัวโดยการเพิ่มสัญญาณรบกวนลงไป (โยนเหรียญออกหัวตอบตามจริง โยนเหรียญออกก้อยตอบสุ่ม) ซึ่งจะทำให้ได้ข้อมูลที่ยังพอนำไปวิเคราะห์ทางสถิติได้อยู่ แต่ก็ยากที่จะย้อนกลับไประบุตัวตนของผู้ให้ข้อมูล … ไม่รู้ว่าทีมออกโจทย์เขียนโจทย์มาแบบนี้มีความเกี่ยวข้องอะไรกับการที่ Google ปลด Timnit Gebru และ Margaret Mitchell นักวิจัยด้านจริยศาสตร์ปัญญาประดิษฐ์หรือเปล่าน้าาา 🤔

โจทย์ปัญหา

ทบทวนโจทย์ซักหน่อย เรามีผู้เข้าแข่งขัน $N=100$ คนที่แต่ละคนเก่ง $S_i$ และมีข้อสอบ $M=10,000$ ข้อที่แต่ละข้อยาก $Q_j$ โดยที่ $S_i$ และ $Q_j$ นั้นถูกสุ่มเลือกมาจากการแจกแจงเอกรูปตั้งแต่ $-3$ ถึง $+3$ โจทย์ไม่ได้ให้ค่า $S_i$ หรือ $Q_j$ กับเราตรงๆ แต่ให้เป็นผลลัพธ์ของการทำข้อสอบเสร็จเรียบร้อยแล้ว ซึ่งก็คือ $A_{i,j}$ ที่บอกว่าผู้เข้าแข่งขันคนที่ $i$ ทำข้อสอบข้อที่ $j$ ได้ถูกต้องหรือไม่

โดยโอกาสที่ผู้เข้าแข่งขันที่เก่ง $S_i$ จะทำข้อสอบความยากระดับ $Q_j$ ได้ถูกต้องนั้น มีความน่าจะเป็นอยู่ที่ $f(S_i-Q_j)$ เมื่อ $f$ คือฟังก์ชันซิกมอยด์ ฟังก์ชันยอดฮิตในสายการพัฒนาปัญญาประดิษฐ์ที่มีนิยามว่า

\[f(x) = \frac1{1+e^{-x}}\]

แต่ก็มีผู้เข้าแข่งขันรายหนึ่งที่เลือกจะโกงข้อสอบ โดยก่อนตอบข้อสอบแต่ละข้อจะอาศัยการโยนเหรียญสมดุลดูว่าออกหัวหรือก้อย หากออกหัวก็จะทำข้อสอบข้อนั้นด้วยความสามารถของตนเอง แต่หากออกก้อยก็จะโกงโดยการแอบไปหาเฉลยที่ถูกต้องแล้วนำมาตอบทันที และหน้าที่ของเราก็คือการตามหาคนโกงคนนี้ให้เจอ

ภาคทฤษฎี

ก่อนอื่นสมมติว่าเราคนมีที่เก่ง $s$ และต้องการคาดเดาคะแนนของเขา เนื่องจากเขาต้องทำข้อสอบเป็นจำนวนมากถึงหมื่นข้อ และการกระจายตัวความยากข้อสอบยังเป็นแบบเอกรูปอีกด้วย ทำให้เราสามารถคาดเดาคะแนนของเขาได้โดยเริ่มจากการสร้างการแจกแจงเอกรูปตั้งแต่ $s-3$ ไปถึง $s+3$ ที่มีสมาชิก $M$ ตัว แล้วนำการแจกแจงดังกล่าวไปผ่านฟังก์ชัน $f$ ซึ่งจะทำให้ได้การแจกแจงของความน่าจะเป็นที่จะตอบข้อสอบถูก แต่เพราะว่าในกรณีนี้ความน่าจะเป็นของการตอบถูกแต่ละข้อมีค่าเท่ากับค่าคาดหวังคะแนนในข้อนั้นพอดี ดังนั้นเมื่อหาผลรวมทั้งหมดของการแจกแจงความน่าจะเป็น ก็จะได้ผลรวมค่าคาดหวังเมื่อทำข้อสอบครบทุกข้อด้วย ซึ่งก็คือคะแนนรวมที่ผู้เข้าแข่งขันควรได้นั่นเอง

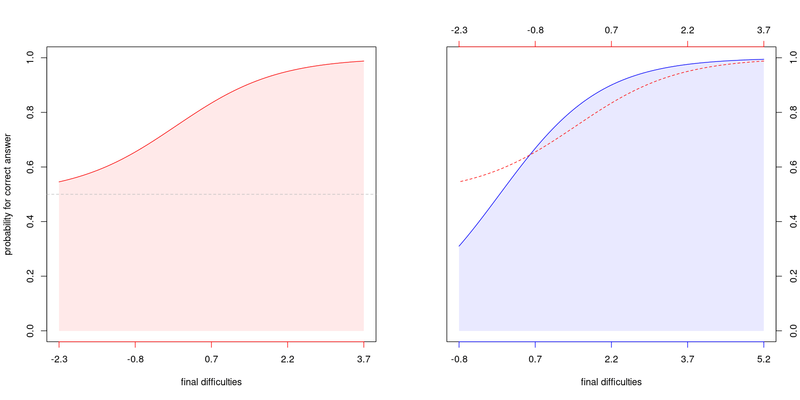
ตัวอย่างการแจกแจงความน่าจะเป็นที่จะตอบถูกของผู้เข้าแข่งขันที่เก่ง $0.7$ เมื่อเจอโจทย์ในช่วงความยากตั้งแต่ $-3$ ไปถึง $+3$

แต่การทำงานกับคะแนนรวมตรงๆ อาจไม่ค่อยเข้าท่าเท่าไหร่ เราจะสนใจสัดส่วนคะแนนรวมต่อคะแนนเต็มแทน ให้ $g_p$ เป็นฟังก์ชันที่รับความเก่งของผู้เข้าแข่งขัน แล้วคำนวณค่า $p$ ซึ่งเป็นค่าคาดหวังของสัดส่วนคะแนนดังกล่าว เมื่อมองการทำงานของมันในมุมแคลคูลัส จะได้ว่า

\[g_p(s) = \frac1{(s+3)-(s-3)} \int\limits_{s-3}^{s+3} f(x) \;dx\]

เนื่องจาก

\[\int f(x) \;dx = \int \frac1{1+e^{-x}} \;dx = \log(1+e^x) {\color[rgb]{.8,.8,.8}\;+C}\]

ดังนั้น

\[g_p(s) = \frac16 \cdot \log\left( \frac{1+e^{s+3}}{1+e^{s-3}} \right)\]

และจะทำให้ได้ฟังก์ชันผกผัน $g_p^{-1}$ ด้วย ซึ่งก็คือฟังก์ชันที่รับค่า $p$ แล้วคำนวณย้อนกลับไปหา $s$ เรียกฟังก์ชันนี้ว่า $g_s$ ซึ่งมีหน้าตาแบบนี้

\[g_s(p) = 3 + \log\left( \frac{1-e^{-6}}{1-e^{-6(1-p)}}-1 \right)\]

ข้อสังเกตถัดมานั่นคือ คนโกงจะใช้ฟังก์ชันความน่าจะเป็นที่จะตอบข้อสอบแตกต่างออกไป ซึ่งได้แก่การรับประกันว่าตอบถูกไปแล้วครึ่งหนึ่งผ่านการโยนเหรียญ ส่วนอีกครึ่งหนึ่งค่อยไปทำข้อสอบตามระดับความเก่งเดิมของตน ให้ $f’$ เป็นฟังก์ชันความน่าจะเป็นที่จะตอบถูกของคนโกง ดังนั้น

\[f'(x) = \frac{1 + f(x)}{2}\]

นั่นหมายความว่าการแจกแจงคะแนนของคนโกงจะมีหน้าตาที่แตกต่างออกไปจากผู้เข้าแข่งขันที่มีความเก่งระดับที่ควรได้คะแนนเท่านั้น ดังนั้นถ้าเราสามารถเทียบคะแนนของผู้เข้าแข่งขันกับโมเดลดังกล่าวได้ ก็จะเดาได้ว่าผู้เข้าแข่งขันคนนั้นโกงหรือไม่

(แดงซ้าย) การแจกแจงความน่าจะเป็นของคนโกงที่เก่ง $0.7$ ซึ่งเทียบเท่าคนสุจริตเก่ง $2.2$ หากพิจาณาเพียงผลรวมคะแนน (น้ำเงินขวา) การแจกแจงความน่าจะเป็นคนสุจริตที่เก่ง $2.2$

ถึงตอนนี้ปัญหาของเราจะเหลือเพียงแค่การหาความยากของข้อสอบแต่ละข้อ แน่นอนว่าเราอาจนำเทคนิคในทำนองเดียวกันกับ $g_p$ มาย้อนคำนวณก็ได้ อย่างไรก็ตามเราจะใช้เพียงแค่การเรียงลำดับข้อสอบตามปริมาณผู้เข้าแข่งขันที่ตอบถูกก็พอ

อนึ่ง เราจะไม่สามารถพิจารณาข้อสอบเป็นรายข้อได้ เนื่องจากข้อสอบแต่ละข้อมีคำตอบจากผู้เข้าแข่งขันเพียงแค่หนึ่งร้อยจุดข้อมูล ซึ่งถือว่าค่อนข้างน้อยและจะทำให้การประมาณความยากเพี้ยนไป เราจะเลี่ยงไปพิจารณาชุดข้อสอบหลายๆ ข้อในช่วงความยากใกล้เคียงกันแทน โค้ดต่อไปนี้จะแบ่งข้อสอบออกเป็น $10$ ชุด ชุดละ $1,000$ ข้อ แล้วเปรียบเทียบดูว่าคำตอบจริงๆ ของผู้เข้าแข่งขันคนนั้นแตกต่างกับโมเดลความเก่งจากคะแนนที่ได้ของผู้เข้าแข่งขันมากน้อยเพียงใด หลังจากนั้นจึงเลือกผู้ที่มีผลรวมของผลต่างกำลังสองมากที่สุดว่าเป็นผู้ต้องสงสัยที่จะโกงข้อสอบนั่นเอง

cumsig <- function(x) log(exp(x)+1)

sumsig <- function(a, b) (cumsig(b)-cumsig(a))/(b-a)

guess <- function(p, k=3, b=exp(-2*k)) k+log((1-b)/(1-b^(1-p))-1)

expect_dist <- function(skill, k=3, bins=10) {
    endpoints <- seq(skill-k, skill+k, length=bins+1)
    sumsig(head(endpoints, -1), tail(endpoints, -1))
}

discrepancy <- function(score, bins=10) {
    theory <- expect_dist(guess(sum(score)/10000), bins=bins)
    actual <- colSums(matrix(score, ncol=bins))*(bins/10000)
    sum((theory-actual)^2)
}

find_cheater <- function(scores) {
    suspects <- apply(scores[order(rowSums(scores)),], 2, discrepancy)
    which(suspects == max(suspects))
}

if (!interactive()) {
    f <- file("stdin", "r")
    cases <- as.integer(readLines(f, n=1))
    percent <- as.integer(readLines(f, n=1))
    for (case in 1:cases) {
        raw <- readLines(f, n=100)
        input <- na.omit(as.integer(unlist(strsplit(raw, ""))))
        answer <- find_cheater(matrix(input, ncol=100))
        cat(paste0("Case #", case, ": ", answer, "\n"))
    }
}

ภาคปฏิบัติ

โค้ดภาคทฤษฎีในหัวข้อที่ผ่านมาแม้จะทำงานได้ แต่ก็ทำได้เพียงแค่พอผ่านเกณฑ์ของการแข่ง Code Jam ที่ $86\%$ เท่านั้น โดยข้อจำกัดหลักของมันคือการที่เราจะจับผิดคนที่เก่งมากๆ อยู่ก่อนแล้วแต่ก็ยังเลือกที่จะโกงเพิ่มไม่ได้ เพราะหน้าตาฟังก์ชัน $f$ และ $f’$ จะคล้ายกันมากจนแพ้สัญญาณรบกวนในข้อมูลจริง

แถมในช่วงการแข่งขันที่มีเวลาจำกัด (หรือแม้กระทั่งในการทำงานจริง?) จะให้มานั่งวิเคราะห์สวยๆ ตั้งแต่แรกนั้นคงเป็นไปได้ยาก … อันที่จริงที่เราวิเคราะห์ $g_s$ ออกมาจนได้นั้นก็ต้องขอบคุณ Wolfram Alpha ที่คอยช่วยแก้สมการหาปฏิยานุพันธ์และฟังก์ชันผกผันให้อยู่ไม่น้อยเลยทีเดียว 🤪

ส่วน ณ ขณะที่เราพยายามแก้ปัญหานี้ สิ่งที่เราทำคือพล็อตข้อมูลผ่านฟังก์ชันต่างๆ เท่าที่คิดออกแล้วสังเกตว่าข้อมูลเหล่านั้นแสดงพฤติกรรมอย่างไร จนสุดท้ายมาลงตัวที่การเรียงความยากข้อสอบตามจำนวนผู้เข้าแข่งขันที่ตอบถูกแล้วแบ่งเป็นชุด (ตามที่เล่าในภาคทฤษฎี) สิ่งที่ต่างออกไปคือเราไม่ได้เอาคะแนนรวมของผู้เข้าแข่งขันแต่ละคนมาย้อนเดาความเก่งของพวกเขาแล้ว แต่แค่เรียงผู้เข้าแข่งขันตามคะแนนรวมก็พอเลย หลังจากนั้นคำนวณค่าเบี่ยงเบนมาตรฐานของคะแนนรวมในแต่ละชุด เมื่อนำไปพล็อตจะเห็นว่าคนที่โกงมีค่าเบี่ยงเบนมาตรฐานต่างไปจากเพื่อนบ้านที่อยู่ในละแวกเดียวกันอย่างชัดเจน ที่เหลือก็แค่พยายามลากเส้นต่อจุดข้อมูลสวยๆ โดยเรานำค่าเบี่ยงเบนมาตรฐานของเพื่อนบ้าน (รวมตนเอง) จำนวน $5$ จุดข้อมูลมาหาค่ามัธยฐาน (ต่อหัวต่อท้ายของข้อมูลเข้าด้วยกันเพื่อให้หาค่าเฉลี่ยที่ขอบได้) แล้วจึงเดาว่าผู้ต้องสงสัยก็คือผู้ที่มีค่าเบี่ยงเบนมาตรฐานของตนแตกต่างออกไปมากที่สุดนั่นแหละ (โค้ดอยู่ในบล็อกตอนที่แล้ว)

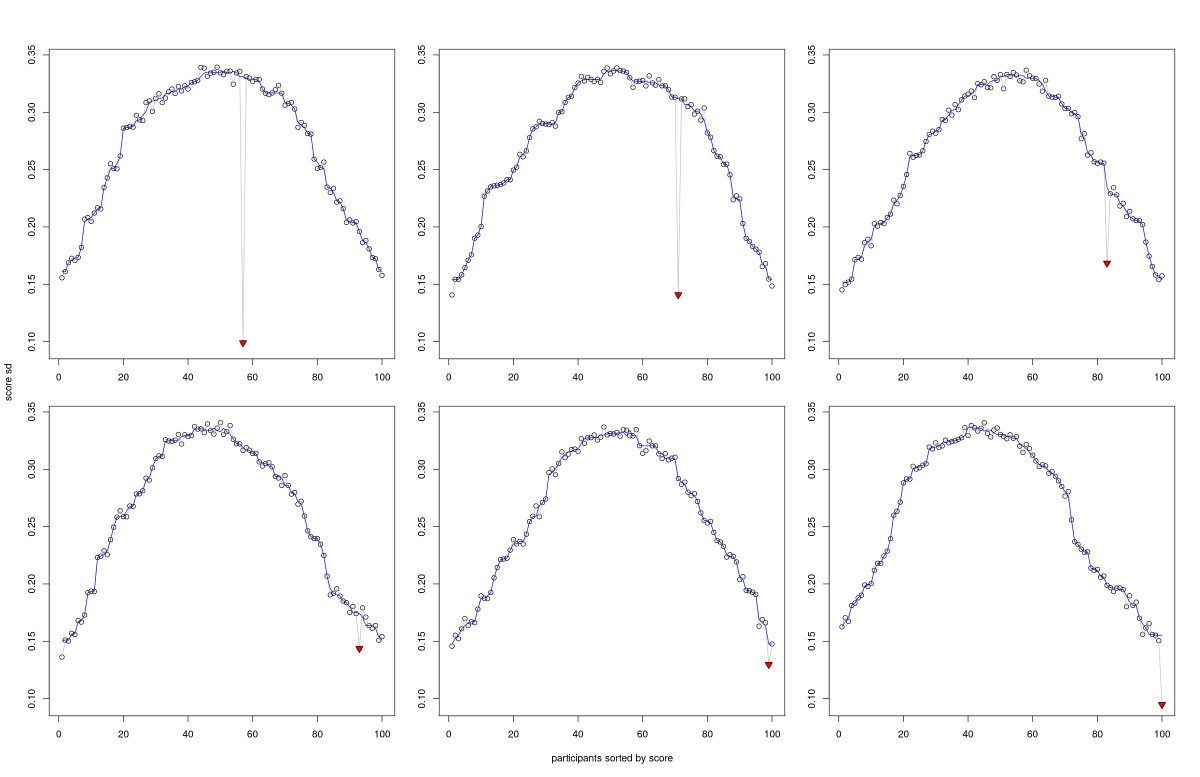
ตัวอย่างข้อมูลจริงที่แสดงค่าเบี่ยงเบนมาตรฐานคะแนนผู้เข้าแข่งขัน โดยเส้นสีน้ำเงินแสดงค่ามัธยฐานในละแวกเพื่อนบ้าน และสามเหลี่ยมสีแดงบ่งบอกข้อมูลของผู้ที่โกงข้อสอบ