สิ่งหนึ่งที่มนุษย์เรามักเข้าใจคลาดเคลื่อนเมื่อต้องเผชิญหน้ากับการสุ่มคือ ความน่าจะเป็น (probability) กับความคาดหวัง (expectation) เป็นคนละเรื่องกัน ยกตัวอย่างเช่นถ้าเรามีลูกเต๋าสมดุลอยู่ลูกหนึ่ง ความน่าจะเป็นที่ทอยลูกเต๋าแล้วจะได้หน้าหนึ่งที่ต้องการคือ $\frac16$ ส่วนความคาดหวังที่ทอยหนึ่งครั้งแล้วจะได้หน้านั้นก็คือ $\frac16$ ครั้ง นี่อาจทำให้เราเข้าใจว่าเมื่อทอยเต๋าไป $6$ ครั้งแล้ว เราต้องได้เต๋าหน้านั้น $6 \cdot \frac16 = 1$ ครั้งแน่ๆ แต่อันที่จริงแล้วนั่นคือค่าคาดหวังต่างหาก ความน่าจะเป็นจริงๆ ที่เราจะทอยเต๋า $6$ ครั้งแล้วออกหน้าที่ต้องการเป็นจำนวน $1$ ครั้งพอดีคือ $\binom{6}{1}(\frac16)^1(\frac56)^5 \approx 40\%$ เท่านั้น

สาเหตที่เรามีความเข้าใจผิดเพี้ยนไป นอกจากจะมาจากความยากของศาสตร์ดังกล่าวในตัวมันเองแล้ว ยังอาจเกิดเพราะความเอนเอียงทางการรู้คิด (cognitive bias) ที่ทำให้เรามักจดจำและให้น้ำหนักกับเหตุการณ์เลวร้ายมากกว่าเหตุการณ์ที่งดงามตามสมควรแก่เหตุอีกด้วย ดังจะเห็นได้จากเกมอย่าง XCOM ที่ใช้การสุ่มเพื่อกำหนดว่าเราจะยิงโดนศัตรูหรือไม่ ซึ่งเรามักเห็นคำบ่นทำนองนี้อยู่บ่อยๆ

โอกาสยิงโดนตั้ง $99\%$ ยังจะพลาดอีก!

ในเมื่อแก้ที่มนุษย์ไม่ได้ บางเกมจึงเลือกที่จะโอนอ่อนต่อพฤติกรรมอันไม่สมเหตุสมผลอันนี้ของมนุษย์เอาซะเลย เช่นในเกมชุด Civilization ที่เมื่อผู้เล่นโจมตีพลาดติดกันหลายครั้งจนครบค่าคาดหวังที่ควรจะโจมตีโดน การโจมตีครั้งนั้นจะกลายเป็นโจมตีโดนโดยอัตโนมัติ¹ เช่น การโจมตีครั้งหนึ่งที่มีความน่าจะเป็นที่จะโจมตีโดนอยู่ที่ $\frac13$ หากผู้เล่นโจมตีพลาดติดกันมาแล้ว $2$ ครั้ง การโจมตีครั้งถัดไปจะการันตีว่าโจมตีโดนอย่างแน่นอน²

แล้วค่าคาดหวังของการโจมตีโดนจะมีหน้าตาเปลี่ยนไปเป็นอย่างไรหละ? ก่อนอื่นมานิยามกติกาชุดใหม่นี้ให้รัดกุมก่อน เพื่อให้วิเคราะห์ได้อย่างเป็นระเบียบต่อไป

เกมหนึ่งใช้ลูกเต๋า $k$ หน้าในการเล่น โดยมีเพียงหน้าเดียวในนั้นที่เมื่อทอยออกแล้วจะได้รางวัล อย่างไรก็ตามหากทอยเต๋าติดกันมา $k-1$ ครั้งแล้วยังไม่ได้รางวัลเลยซักครั้ง การทอยเต๋าครั้งหน้าจะถือว่าได้รับรางวัลทันที เกมนี้มีค่าคาดหวังที่จะได้รางวัลเป็นสัดส่วนเท่าไหร่ต่อการทอยเต๋าทั้งหมด (เพื่อความสะดวก สนใจเฉพาะกรณีที่ทอยเต๋าเป็นจำนวนมากเข้าใกล้อนันต์ครั้งก็ได้)

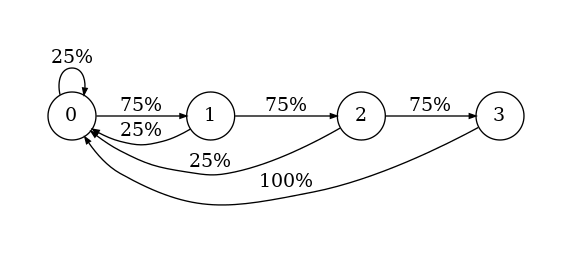
เราอาจมองกระบวนการทั้งหมดเป็นลูกโซ่มาร์คอฟที่มี $k$ สถานะ³ โดยแต่ละสถานะจะจำไว้ว่าเคยโยนลูกเต๋าที่ทำให้ไม่ได้รางวัลติดกันมาแล้วกี่ครั้ง ซึ่งจะเห็นว่าการเปลี่ยนจากสถานะ $k-1$ ไปยังสถานะ $0$ มีความน่าจะเป็นเท่ากับ $1$ ส่วนการเปลี่ยนจากสถานะ $i$ อื่นๆ ไปยังสถานะ $0$ มีความน่าจะเป็นอยู่ที่ $\frac1k$ และการเปลี่ยน​ไปยังสถานะ $i+1$ มีความน่าจะเป็น $\frac{k-1}k$ นั่นเอง

ตัวอย่างลูกโซ่มาร์คอฟของการทอยลูกเต๋าสี่หน้าในเกมนี้

หรือเขียนเป็นเมทริกซ์การเปลี่ยนสถานะที่มีมิติ $k \times k$ ได้คือ

\[M = \begin{bmatrix} \frac1k & \frac{k-1}k & 0 & 0 & \cdots & 0 \\ \frac1k & 0 & \frac{k-1}k & 0 & & 0 \\ \frac1k & 0 & 0 & \frac{k-1}k & & 0 \\ \vdots & & & & \ddots & \vdots \\ \frac1k & 0 & 0 & 0 & &\frac{k-1}k \\ 1 & 0 & 0 & 0 & \cdots & 0 \\ \end{bmatrix}\]

ให้ $\vec{u}_0$ เป็นเวกเตอร์ที่เก็บการกระจายตัวของสถานะตอนเริ่มต้นเกม ดังนั้นการกระจายตัวของสถานะหลังจากทอยเต๋าไปแล้ว $n$ รอบ (เขียนแทนด้วย $\vec{u}_n$) สามารถคำนวณได้จาก

\[\vec{u}_0 \cdot M^n = \vec{u}_n\]

จะเห็นว่าเมื่อ $n \to \infty$ แล้ว $\vec{u}_n$ จะลู่เข้าค่าคงที่ค่าหนึ่ง เราเรียกสถานะนี้ว่าสภาวะคงตัวและเขียนแทนด้วย $\vec{v}$ นอกจากนี้เราจะได้อีกว่า

\[\vec{v} \cdot M = \vec{v}\]

หรือก็คือ $\vec{v}$ เป็นเวกเตอร์ลักษณะเฉพาะของ $M$ ที่จับคู่กับค่าลักษณะเฉพาะที่เท่ากับหนึ่ง และเราสามารถแก้สมการหาค่าดังกล่าวได้คือ

\[\begin{align} \vec{v} &= \begin{bmatrix}v_0 & v_1 & v_2 & \cdots & v_{k-1}\end{bmatrix} \\ v_i &= \frac1k \cdot \frac1{1-\left(1-\frac1k\right)^k} \cdot \left(\frac{k-1}{k}\right)^i \end{align}\]

ซึ่งคำตอบนี้ตีความได้ว่า หลังจากทอยเต๋าไปเป็นจำนวนมากครั้งจนเข้าสู่สภาวะคงตัวแล้ว การกระจายตัวของสถานะจะมีหน้าตาเป็นเวกเตอร์ $\vec{v}$ และเมื่อทอยเต๋าเพิ่มอีกหนึ่งครั้งจากสถานะดังกล่าว จะมีการทอยเป็นสัดส่วนเท่ากับ $v_0 = 1/k(1-(1-\frac1k)^k)$ ที่ได้รางวัล ซึ่งก็คือค่าคาดหวังใหม่ที่เราต้องการหานั่นเอง

หน้าลูกเต๋า	รางวัลต่อการทอย (กติกาเดิม)	รางวัลต่อการทอย (กติกาใหม่)
1	$\frac11 = 100\%$	$\frac11 = 100\%$
2	$\frac12 = 50\%$	$\frac23 \approx 67\%$
3	$\frac13 \approx 33\%$	$\frac9{19} \approx 47\%$
4	$\frac14 = 25\%$	$\frac{64}{175} \approx 37\%$
5	$\frac15 = 20\%$	$\frac{625}{2101} \approx 30\%$
6	$\frac16 \approx 17\%$	$\frac{7776}{31031} \approx 25\%$

ตัวเลขที่วิเคราะห์ออกมาก็สวยดี แต่นี่ก็เป็นเพียงแค่มุมมองหนึ่งทางคณิตศาสตร์เท่านั้น เพราะหากย้อนกลับไปมองปัญหาตั้งแต่ต้นทางแล้ว จะพบว่าการโจมตีแต่ละครั้งในเกมเหล่านั้นมีล้วนเป็นตัวตัดสินชี้เป็นชี้ตายของการต่อสู้ เพราะหากเราเป็นฝ่ายเปิดยิงก่อนแล้วดันพลาด ศัตรูย่อมอาศัยโอกาสดังกล่าวเคลื่อนพลไปยังตำแหน่งที่ดีกว่า เพื่อยิงสวนกลับมาด้วยความแม่นยำที่เรียกว่าทำให้เราปิดเกมไปนอนพักได้เลย

หรืออันที่จริงแล้ว ข้อมูลความน่าจะเป็นที่จะโจมตีเข้าเป้านั้นไม่ใช่สิ่งที่ตอบโจทย์ตั้งแต่แรก แต่ควรเป็นข้อมูลว่าหากการโจมตีครั้งนี้ไม่สำเร็จ เรายังมีโอกาสได้ไปต่อจากความผิดพลาดนี้มากน้อยแค่ไหน ซึ่งอาจสะท้อนออกมาจากการที่เกมแสดงตัวเลขความน่าจะเป็นของการโจมตีให้น้อยกว่าความเป็นจริงตั้งแต่แรก เพื่อสะกิดให้เรากลับไปทบทวนการโจมตีตอนที่เห็นว่าแผนมีโอกาสสำเร็จเพียง $50\%$ ทั้งที่ในความจริงแล้วมันอาจมีโอกาสสำเร็จมากถึง $80\%$ ก็ได้ แต่เพราะว่าเราไม่สามารถยอมรับความล้มเหลวได้แม้มันจะมีโอกาสน้อยนิดเพียง $1\%$ ก็ตาม ซึ่งก็คล้ายกับวิธีที่เกมชุด Fire Emblem เลือกใช้นั่นเอง

Originally published on: Facebook