เล่นแลกของขวัญให้ไม่ได้ของตัวเอง
เคยตั้งข้อสังเกตกว่าครึ่งทศวรรษไว้ว่า งานปาร์ตี้แลกของขวัญมักมีคนที่ได้ของขวัญของตัวเองอยู่บ่อยๆ ซึ่งจากการวิเคราะห์ความน่าจะเป็นทำให้เห็นว่าโอกาสที่งานปาร์ตี้หนึ่งๆ จะไม่มีใครได้ของขวัญของตัวเองเลยนั้นลู่เข้าหา $1/e$ แต่ก็ยังเหลือคำถามสำคัญที่ตอนนั้นตอบไม่ได้คือ แล้วเราจะมีวิธีแลกของขวัญที่แฟร์และไม่มีใครได้ของขวัญของตัวเองมั้ย?
ก่อนอื่นระลึกกันอีกครั้งว่า จากคนที่มาเล่นเกมแลกของขวัญกัน $n$ คน จำนวนวิธีการการแลกของขวัญที่ไม่มีใครได้ของตัวเองมีทั้งหมด
\[\begin{align} d(0) &= 1 \\ d(1) &= 0 \\ d(n) &= (n-1) \Big( d(n-1) + d(n-2) \Big) = \left\lceil \frac{n!}e \right\rfloor \end{align}\]แต่เพราะจำนวนวิธีการแลกของขวัญทั้งหมดที่สามารถมีคนได้ของตัวเองได้คือ $n!$ ดังนั้น $d(n)/n! \approx 1/e$ หรือประมาณ $36\%$ นี่ทำให้เรามีขั้นตอนวิธีที่ง่ายดายสำหรับการแลกของขวัญที่ไม่มีใครได้ของตัวเอง ซึ่งก็คือการสุ่มแลกของขวัญไปเรื่อยๆ จนครบทุกคนนั่นแหละ แต่ถ้าระหว่างทางมีใครจับได้ของขวัญของตัวเองก็จะต้องกลับไปเริ่มการแลกของขวัญใหม่ตั้งแต่ต้น (ถ้าไม่โละกระดานเริ่มใหม่จะได้ผลลัพธ์ที่ไม่แฟร์) เนื่องจากโอกาสที่จะไม่มีใครได้ของขวัญของตัวเองเป็นค่าคงที่ประมาณหนึ่งในสาม ดังนั้นโดยเฉลี่ยแล้วเราจะเริ่มใหม่ประมาณสามรอบถึงจะเจอการแลกของขวัญที่ต้องการ
แม้วิธีข้างต้นจะถือว่าไม่เลวในมุมมองอัลกอริทึมสำหรับคอมพิวเตอร์ แต่หากนำไปใช้งานจริงในปาร์ตี้ก็อาจจะดูแปลกจนน่าเวียนหัว เพราะระหว่างทางที่แลกของขวัญ คนที่ร่วมเล่นเกมจะได้กล่องของขวัญของคนอื่นมาวางไว้ตรงหน้าด้วยความตื่นเต้นแล้ว แต่ก็ยังเปิดกล่องของขวัญไม่ได้จนกว่าการแลกของขวัญจะสิ้นเสร็จถูกต้องสมบูรณ์จนถึงคนสุดท้าย และยังมีโอกาสสูงมากที่จะต้องโบกมือลาบ๊ายบายกล่องของขวัญที่แลกมาระหว่างทางเพราะต้องเริ่มเล่นแลกของขวัญใหม่ทั้งหมดอีกรอบด้วย
เราอาจเปลี่ยนไปใช้วิธีของ Hannah Fry ในวิดีโอ Secret Santa ก็ได้ ซึ่งให้ผลลัพธ์การแลกของขวัญที่ทุกคนมีโอกาสได้ของคนอื่นเท่าๆ กันโดยไม่มีโอกาสได้ของตัวเองเลย แต่กระบวนการดังกล่าวจะให้ผลลัพธ์ไม่ครอบคลุมวิธีการแลกของขวัญทั้งหมด เพราะมีเพียงแค่การแลกของขวัญเป็นวงกลมวงใหญ่เพียงวงเดียวเท่านั้นที่สามารถเป็นผลลัพธ์ได้ ในขณะที่วิธีการแลกของขวัญทั้งหมดสามารถมีวงแลกของขวัญย่อยๆ ได้หลายวงเลย
และแม้วิธีดังกล่าวจะมีขั้นตอนเรียบง่ายทั้งยังให้ผลลัพธ์ที่ถือว่าแฟร์แล้ว แต่จุดตายสำคัญคือการออกแบบวิธีที่ขาดส่วนร่วมจากผู้เล่นแต่ละคนที่อุตสาห์เฟ้นหาของขวัญมาเล่นเกมนี้ เพราะขั้นตอนวิธีดังกล่าวอาศัยเพียงแค่กรรมการหนึ่งคนก็เพียงพอแล้วที่จะจัดเรียงหาว่าใครควรได้ของขวัญจากใคร ผู้เล่นแต่ละคนแค่นำกล่องของขวัญมาวางไว้ตอนเริ่มปาร์ตี้แล้วก็หยิบกล่องของขวัญตามคำบอกกลับบ้านตอนจบปาร์ตี้ได้เลย ไม่ต้องออกแรงสุ่มด้วยตนเองใดๆ ทั้งสิ้น
เช่นนี้แล้วเราจะสิ้นหวังหาทางออกที่บาลานซ์ระหว่างความถูกต้องทางคณิตศาสตร์และความสนุกตื่นเต้นเร้าใจและมีส่วนร่วมของมนุษย์ให้กับเรื่องนี้ไม่ได้เลยหรือ? โชคดีที่ Nat Sothanaphan ส่งข่าวว่ามาว่าเปเปอร์ [Martínez-Panholzer-Prodinger 2008] ได้เขียนรายละเอียดการสร้างลำดับสุ่มโดยห้ามของอยู่ซ้ำที่เดิมในแง่มุมทางคณิตศาสตร์ไปเรียบร้อยแล้ว ซึ่งใจความสำคัญสามารถสรุปเป็นโค้ด Python ได้ดังนี้
import random
def d(n, memo={0: 1, 1: 0}):
if n not in memo:
memo[n] = (n-1) * (d(n-1) + d(n-2))
return memo[n]
def random_close_loop(r):
return random.choices([True, False], weights=[d(r-1), d(r)])[0]
def derangement(n):
if n == 1:
raise Exception('can not do derangement with only 1 item')
hat = set(range(n))
result = list(range(n))
for i in range(n):
if i in hat:
hat -= {i}
j = random.choice(list(hat))
result[i], result[j] = result[j], result[i]
if random_close_loop(len(hat)):
hat -= {j}
return result
หรือเล่าเป็นขั้นตอนให้คนทั่วไปที่อยากลองเอาไปทดลองตามได้ว่า
- เตรียมฉลากที่มีชื่อคนทุกคนที่จะเล่นแลกของขวัญใส่ไหจับฉลาก
- ประธานจับฉลากหนึ่งใบ (ไม่ใส่คืน) เพื่อหาคนเริ่มต้นวงจับของขวัญ (หรือจบเกมเมื่อไม่เหลือฉลาก)
- เอาของขวัญของคนที่มีชื่อบนฉลากมาวางบนแท่นของขวัญสำหรับการจบรอบวงย่อย
- ให้คนที่มีชื่อบนฉลาก เป็นคนจับฉลากใบถัดไปเพื่อหาว่าเขาจะได้รับของขวัญจากใคร
- คนจับฉลากในข้อที่ผ่านมารับของขวัญจากคนที่มีชื่อบนฉลากในข้อที่ผ่านมา
- นับจำนวนคนที่เหลือที่ยังไม่ได้ของขวัญแล้วให้เป็นค่า $r$ (ไม่ต้องนับคนที่เพิ่งได้ของขวัญในข้อที่แล้ว)
- คนที่มีชื่อบนฉลาก โยนเหรียญไบแอสที่มีน้ำหนักดังนี้
- ออกก้อยด้วยน้ำหนัก $d(r)$ ไม่มีเหตุการณ์ที่น่าสนใจเกิดขึ้น แค่วนกลับไปทำข้อ 4. ไล่ลงมา
- ออกหัวด้วยน้ำหนัก $d(r{-}1)$ ถือว่าได้ของขวัญจบวงย่อย ดังนั้นวนกลับไปทำข้อ 2. ไล่ลงมา
- ประธานกล่าวปิดงาน 😝
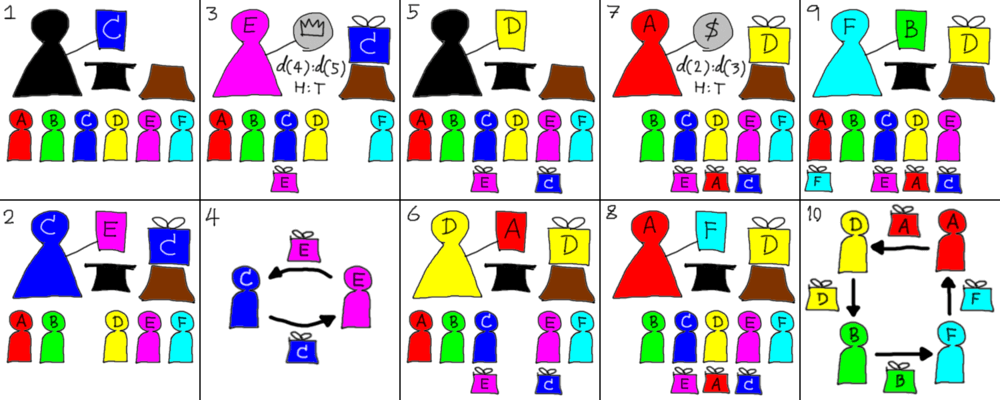
ตัวอย่างการสุ่มแลกของขวัญที่ไม่มีใครได้ของตัวเองเมื่อ $n=6$ ผลลัพธ์นี้ได้วงย่อยของการแลกของขวัญเป็นจำนวนสองวง
จากตัวอย่างการแลกของขวัญของกลุ่มคนหกคนในรูปข้างต้น อธิบายแต่ละขั้นตอนได้คือ
- ประธานจับฉลากใบแรกเพื่อหาคนเริ่มต้นวงย่อยการแลกของขวัญ ซึ่งก็คือน้ำเงิน
- น้ำเงินนำกล่องของขวัญตัวเองมาวางไว้บนแท่น พร้อมจับฉลากใบถัดไปและได้ชมพู
- เพราะตอนนี้ $r=5$ ชมพูโยนเหรียญด้วยน้ำหนักหัว $d(4)$ ต่อน้ำหนักก้อย $d(5)$ และออกหัว
- ชมพูได้รับของขวัญบนแท่น และปิดวงย่อยของการแลกของขวัญที่มีแค่สองคน 💏
- ประธานจับฉลากอีกครั้งเพื่อหาคนเริ่มวงย่อยเพื่อแลกของขวัญรอบถัดไป ซึ่งคราวนี้ได้เหลือง
- เหลืองเอาของขวัญตัวเองมาวางแท่น แล้วจับฉลากได้แดง
- แดงโยนเหรียญด้วยน้ำหนักออกหัว $d(2)$ ต่อน้ำหนักออกก้อย $d(3)$ และออกก้อย
- แดงอดได้ของขวัญบนแท่น จึงต้องจับฉลากและจับได้ฟ้า
- เหลือสองคนสุดท้าย ฟ้าไม่จำเป็นต้องโยนเหรียญแล้ว เพราะน้ำหนักออกหัวคือ $d(1)=0$ จึงต้องจับฉลากแน่นอน และฉลากก็เหลือเพียงใบเดียวฟ้าจึงไม่มีทางเลือกนอกจากได้ของขวัญจากเขียว (ส่วนเขียวก็ไม่ต้องทำอะไรเพราะน้ำหนักโยนเหรียญออกก้อยคือ $d(1)=0$ ซึ่งก็คือต้องรับของขวัญบนแท่นนั่นเอง)
- สรุปผลวงย่อยของการแลกของขวัญวงที่สอง ที่มีคนสี่คนแลกของขวัญกันเป็นวงตามรูป 👨👩👧👧
อย่างไรก็ตาม เราคงไม่สามารถหาเหรียญที่ปรับน้ำหนักของแต่ละด้านอย่างละเอียดตามที่อัลกอริทึมต้องการได้ หรือถ้าจะย้ายไปคำนวณเชิงตัวเลขล้วนๆ ด้วยคอมพิวเตอร์เพียง ก็อาจนำมาซึ่งปัญหาเรื่องความเชื่อใจของมนุษย์ต่อเครื่องจักรและ RNGsus แทนอีก เช่นนี้แล้วเราควรทำอย่างไรดี?
สังเกตว่าสำหรับแต่ละค่า $r$ ความน่าจะเป็นของการโยนเหรียญออกหัวคือ
\[\begin{array}{c|cc|cl} r & \text{weight H} & \text{weight T} & P(\text{toss H}) \\ \hline 1 & 1 & 0 & \dfrac1{1+0} = 1 \\ 2 & 0 & 1 & \dfrac0{0+1} = 0 \\ 3 & 1 & 2 & \dfrac1{1+2} = \dfrac13 \\ 4 & 2 & 9 & \dfrac2{2+9} = \dfrac2{11} & \approx \dfrac15 \;\;\text{(error $9\%$)} \\ 5 & 9 & 44 & \dfrac9{9+44} = \dfrac9{53} & \approx \dfrac16 \;\;\text{(error $2\%$)} \\ 6 & 44 & 265 & \dfrac{44}{44+265} = \dfrac{44}{309} & \approx \dfrac17 \\ \vdots & & & \vdots \\ r & d(r{-}1) & d(r) & \dfrac{d(r{-}1)}{d(r{-}1)+d(r)} & \approx \dfrac1{1+r} \end{array}\]นอกจากที่ค่า $r$ น้อยมากๆ แล้ว จะเห็นว่าโอกาสออกหัวอยู่ที่ประมาณ $\frac1{1+r}$ ซึ่งเราสามารถมาถึงข้อสรุปนี้ได้จาก สมการ $d(r) = \left\lceil \frac{r!}e \right\rfloor$ ที่แสดงให้เห็นว่า
\[\frac{d(r{-}1)}{d(r{-}1) + d(r)} \approx \frac{(r{-}1)!}{(r{-}1)! + r!} = \frac{(r{-}1)!}{(r{-}1)!(1{+}r)} = \frac1{1+r}\]จากค่าประมาณอัตราส่วนสวยๆ เช่นนี้ หมายความว่าเราสามารถนำไพ่มาช่วยในการสุ่มได้! ซึ่งเป็นผลดีทางจิตวิทยาของมนุษย์มากกว่าเพราะมันทำให้เราเข้าใจความน่าจะเป็นได้แจ่มชัดกว่าการเห็นเพียงแค่ตัวเลข1 และวิธีการใช้งานมันก็ง่ายดายยิ่งกว่าการหาเหรียญไบแอสมาโยนเป็นไหนๆ เช่นเมื่อ $r=6$ เราสามารถใช้ไพ่เพียงเจ็ดใบที่หนึ่งในนั้นเป็นหน้าโจ๊กเกอร์ได้เลย หากสับไพ่แล้วเปิดเจอโจ๊กเกอร์ก็คือการแลกของขวัญในวงย่อยวงนี้ถึงที่สิ้นสุดนั่นเอง
ข้อสังเกตสำคัญคือกรณีที่ $r=4$ จะเห็นว่าแม้ค่าประมาณนั้นจะมีหน้าตาไล่เลขลดลงมาเรื่อยๆ มาอย่างสวยงาม แต่ความเพี้ยนของการประมาณที่จุดนี้สูงถึงเกือบ $10\%$ ดังนั้นเราจึงควรใช้อัตราส่วน $2:9$ ที่หมายถึงมีโจ๊กเกอร์สองใบต่อไพ่อื่นๆ อีกเก้าใบถึงจะให้ผลลัพธ์การสุ่มที่แฟร์กว่า
def random_close_loop_approx(r):
if r > 4:
return random.choices([True, False], weights=[1, r])[0]
if r == 4:
return random.choices([True, False], weights=[2, 9])[0]
if r == 3:
return random.choices([True, False], weights=[1, 2])[0]
if r == 2:
return False
if r == 1:
return True
raise KeyError('undefined behavior')
แล้วทำไมถึงต้องมีการสุ่มเพื่อปิดวงเช่นนี้ด้วยหละ? ย้อนกลับไปตีความการสร้างคำตอบจากสมการเวียนเกิดเมื่อเพิ่มของชิ้นที่ $k$ เข้าไป จะเห็นว่า
\[d(k) = (k-1) \Big( \underbrace{d(k-1)}_\text{EXISTS} + \underbrace{d(k-2)}_\text{CREATE} \Big)\]- EXISTS อาจจะมีวงย่อยมาก่อนกี่วงก็ได้ แล้วของชิ้นที่ $k$ เข้าไปแทรกในวงย่อยวงใดวงหนึ่งที่เคยมี
- CREATE สร้างวงย่อยใหม่ซึ่งมีของเพียงสองชิ้นพอดี คือชิ้นที่ $k$ กับอีกชิ้นที่มาก่อน $k$ ที่ถูกเลือกมาอย่างสุ่ม (อย่างไรก็ตาม เมื่อใส่ของชิ้นหลังจาก $k$ ไปเรื่อยๆ วงนี้อาจถูกขยายขนาดทีหลังได้)
แต่สิ่งที่อัลกอริทึมสุ่มลำดับไม่ซ้ำที่เดิมทำนั้น จะเปลี่ยนเป็นวิ่งสวนทางโดยลดค่า $k$ ลงเรื่อยๆ แทน ดังนั้นเราต้องตีความการ CREATE กลับด้าน โดยหมายความว่าหลังจากพิจารณาของชิ้นที่ $k$ ออกมาแล้ว เราจะเหลือของอยู่ $r=k-1$ ชิ้น และเราจะถามต่อทันทีว่าของชิ้นต่อไปที่จะเอาออกควรย้อนกลับไปปิดวงย่อยที่มีของชิ้นที่ $k$ หรือเปล่า ซึ่งสัดส่วนจำนวนเหตุการณ์ที่เกิดก็คือ $\frac{\abs{\text{CREATE}}}{\abs{\text{CREATE}}+\abs{\text{EXISTS}}}$ นั่นเอง
หวังว่าจะได้ทริกดีๆ ไว้ทำให้ปาร์ตี้แลกของขวัญสนุกยิ่งขึ้นนะ 🃏

author