เมื่อพูดถึงดาวเทียมที่มนุษยชาติส่งขึ้นไปยังอวกาศ เราคงมีภาพจำว่ามันมักโคจรที่รอบโลกเป็นวงกลมบ้างวงรีบ้าง ไม่งั้นก็อาจไปโคจรรอบดาวเคราะห์อื่นๆ หรือดวงอาทิตย์เป็นแน่ แต่ยังมีดาวเทียมอีกประเภทหนึ่งซึ่งถูกส่งไปโคจรรอบจุดลากรองจ์ ซึ่งเป็นตำแหน่งสมมติที่ได้มาจากการคำนวณ เพราะในความเป็นจริงแล้วมันคือความว่างเปล่าในอวกาศไม่มีสิ่งใดให้ยึดเหนี่ยว!

ในแง่หนึ่ง หากจะบอกว่าดาวเทียมเหล่านั้นโคจรรอบจุดลากรองจ์ก็คงไม่ถูกเสียทีเดียว เพราะมันฉกฉวยใช้ประโยชน์จากระบบเทหวัตถุสองชิ้นที่โคจรรอบกัน โดยทั้งคู่นั้นต้องมีมวลมากกว่าตัวดาวเทียมมากๆ (เพื่อเลี่ยงความโกลาหลจากปัญหาสามเทหวัตถุ) และหนึ่งในเทหวัตถุก็ควรมีมวลคิดเป็นเกือบทั้งหมดของระบบด้วย เช่น คู่เทหวัตถุโลก-ดวงจันทร์, ดวงอาทิตย์-โลก, ดวงอาทิตย์-ดาวพฤหัส โดยดาวเทียมจะไปโคจรรอบจุดศูนย์กลางมวลด้วยความเร็วเชิงมุมของระบบนั่นเอง

แล้วการที่เราเอาดาวเทียมไปโคจรอยู่ ณ ตำแหน่งสมมติที่เป็นอวกาศว่างเปล่า วงโคจรของดาวเทียมเหล่านั้นจะไม่มีปัญหาด้านความเสถียรหรือ? เอาจริงก็พอมีปัญหาอยู่บ้างแต่นับว่าเบากว่าบริเวณอื่น เพราะว่าจุดลากรองจ์เป็นจุดที่เราเลือกให้แรงต่างๆ หักล้างกันหมดพอดียังไงหละ

ซึ่งแรงตัวแรกที่เราสนใจและรู้จักกันดีก็คงหนีไม่พ้นแรงโน้มถ่วง จากกฎความโน้มถ่วงสากลของนิวตัน เราทราบว่าแรงโน้มถ่วงที่วัตถุสองชิ้นกระทำต่อกันนั้นมีขนาดเท่ากับ

\[F = \frac{Gm_1m_2}{r^2}\]

เพราะว่าเรามีเทหวัตถุหลักสองตัวกระทำต่อดาวเทียม เราจึงมีแรงโน้มถ่วงสองแรง สนใจคู่เทหวัตถุดวงอาทิตย์-โลก ให้สัญลักษณ์ $\odot,\oplus,\varepsilon$ แทนดวงอาทิตย์ โลก และดาวเทียมตามลำดับ ดังนั้นเราจึงมี

\[F_\odot = \frac{Gm_\odot m_\varepsilon}{r_{\odot\varepsilon}^2} \quad\quad\text{and}\quad\quad F_\oplus = \frac{Gm_\oplus m_\varepsilon}{r_{\oplus\varepsilon}^2}\]

เมื่อคำนึงถึงความเป็นเวกเตอร์ของแรง จะได้ว่าทิศทางของแรงโน้มถ่วงที่กระทำต่อดาวเทียมนั้นชี้พุ่งเข้าหาเทหวัตถุหลักชิ้นนั้นๆ

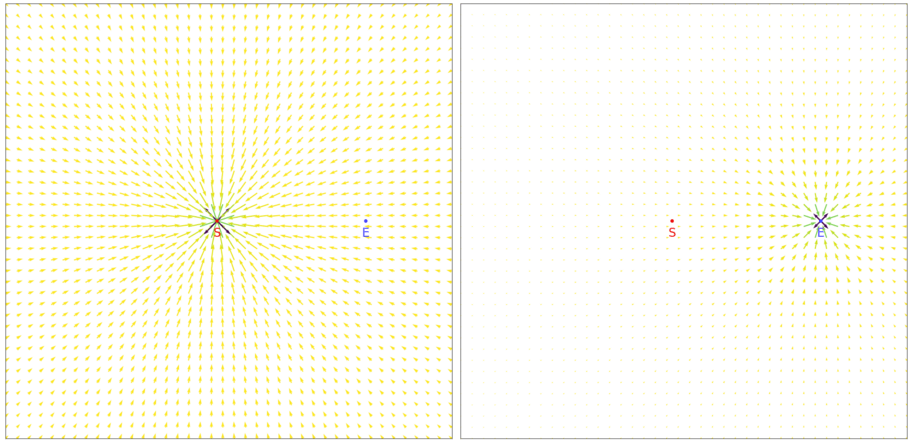
แรงโน้มถ่วงจากดวงอาทิตย์ (ซ้าย) และจากโลก (ขวา) ต่อจุดต่างๆ – ภาพระยะห่างและมวลไม่ตรงสเกล¹

เนื่องจากระบบของเทหวัตถุคู่นี้มีความสมดุลจากการหมุนรอบตัวเอง เพื่อความเรียบง่ายเน้นไอเดียหลักของการคำนวณ เราจะถือว่าวงโคจรของคู่เทหวัตถุหลักนั้นเป็นวงกลมพอดี เลือกจุดศูนย์กลางมวลเป็นจุดหมุนอ้างอิง จากกฎของเคปเลอร์ ได้ว่าความเร็วเชิงมุมของระบบนั้นคำนวณได้จาก

\[\omega^2 = \frac{G(m_1+m_2)}{r^3}\]

ซึ่งเมื่อเราพิจารณาผ่านกรอบอ้างอิงที่หมุนอยู่เช่นนี้แล้ว ก็จะมีแรงเทียมโผล่เข้ามาด้วย แรงเทียมตัวแรกที่มีผลมากที่สุดคือแรงเหวี่ยงหนีศูนย์กลางแบบเรารู้สึกได้ตอนขับรถเข้าโค้งนั่นเอง แรงนี้จะกระทำต่อดาวเทียมตามระยะห่างจากจุดศูนย์กลางการหมุน โดยมีทิศทางเวกเตอร์ชี้ออกจากจุดนั้น และคำนวณขนาดได้เท่ากับ

\[F = m\omega^2r\]

หรือเมื่อแทนค่า $\omega^2$ ในกรณีของดวงอาทิตย์-โลกลงไป จะได้

\[F_c = \frac{G(m_\odot + m_\oplus)rm_\varepsilon}{r_{\odot\oplus}^3}\]

แรงเหวี่ยงหนีศูนย์กลางของระบบดวงอาทิตย์-โลก ที่หมุนรอบจุดศูนย์กลางมวลของเทหวัตถุทั้งสอง

จริงๆ ยังมีแรงที่สำคัญอีกตัวที่ส่งผลต่อระบบเทหวัตถุที่หมุนรอบตัวเอง อันได้แก่แรงคอริออลิสซึ่งเป็นแรงเทียมที่คอยเบี่ยงเส้นทางของวัตถุที่โคจรเข้าหาหรือออกจากจุดศูนย์กลาง เหมือนกับตอนที่เมฆจากขั้วโลกเมื่อเคลื่อนที่เข้าหาเส้นศูนย์สูตรจะเบี่ยงไปไปทางทิศตะวันตกนั่นเอง แต่เนื่องจากจุดลากรองจ์ถูกออกแบบให้เป็นจุดที่หยุดนิ่งเมื่อเทียบกับระบบที่กำลังหมุน เราจึงสามารถตัดแรงนี้ทิ้งไปได้ในการคำนวณอย่างง่าย และจะได้ว่าจุดลากรองจ์คือจุดที่สมการนี้เป็นจริงนั่นเอง

\[\begin{equation} \vec{F_\odot} + \vec{F_\oplus} + \vec{F_c} = 0 \label{eq:zero-force}\tag{1} \end{equation}\]

สนามเวกเตอร์และคอนทัวร์แสดงผลรวมของแรงหลักทั้งสาม (คอนทัวร์นี้ต่างจากที่อื่นๆ ที่พล็อตพลังงานศักย์ซึ่งเป็นปริพันธ์ของแรง)

จุด L1, L2, L3

อยากจะรู้ตำแหน่งเป๊ะๆ ของจุดลากรองจ์ก็ต้องแก้สมการเวกเตอร์ $\eqref{eq:zero-force}$ ซึ่งถ้าเราพิจารณาแบบเวกเตอร์เลยก็นับว่ายากอยู่ แต่เนื่องจากขนาดของแรงไม่ติดลบ เราจะลดรูปมาพิจารณากรณีที่แรงทั้งหมดอยู่บนเส้นตรงเดียวกันก่อน โจทย์ก็จะเหลือเพียงแค่ว่าแรงแต่ละแรงชี้ไปในทิศทางบวกหรือลบเท่านั้น ซึ่งก็คือเราจะแก้สมการในหน้าตาแบบนี้

\[\pm F_\odot \pm F_\oplus \pm F_c = 0\]

โดยที่เครื่องหมาย $\pm$ ทั้งสามตัวจะเป็นบวกพร้อมกันสองตัวและตัวที่เหลือเป็นลบ เมื่อแทนวิธีคำนวณแรงต่างๆ ลงไปในสมการ จะเหลือว่า

\[\pm \frac{m_\odot}{r_{\odot\varepsilon}^2} \pm \frac{m_\oplus}{r_{\oplus\varepsilon}^2} \pm \frac{(m_\odot + m_\oplus)r}{r_{\odot\oplus}^3} = 0\]

ซึ่งเป็นพหุนามกำลังห้าทำให้ไม่มีวิธีหาคำตอบในรูปปิด แต่เราอาจเลือก $\alpha = m_\oplus/(m_\odot{+}m_\oplus)$ แล้วใช้เทคนิคประมาณค่าโดยคำนึงว่าสัดส่วน $\alpha$ มีค่าน้อยจนเข้าใกล้ศูนย์ เมื่อแก้สมการแต่ละชุดออกมาจะได้ว่าระยะทางจากจุดหมุนไปยังจุดลากรองจ์ต่างๆ มีค่าประมาณ

\[\frac{r}{r_{\odot\oplus}} \approx \left(1-\sqrt[3]\frac\alpha3\right),\;\; \left(1+\sqrt[3]\frac\alpha3\right),\;\; \left(-1-\frac{5}{12}\alpha\right)\]

ซึ่งเราเรียกชื่อจุดลากรองจ์แต่ละจุดนี้ว่า L1, L2, L3 ตามลำดับ โดยสองจุดแรกมีความสำคัญ คือ เป็นตำแหน่งสำหรับดาวเทียมหลายสิบดวงที่ต้องการสมบัติของการไม่โคจรรอบโลก อาจจะเพื่อให้มองดวงอาทิตย์ได้ก่อนโลก มองโลกแบบที่มีแสงแดดตกกระทบตลอดเวลา หรือมองห้วงอวกาศลึกโดยไม่ต้องกลัวโลกมาบดบัง

จุด L4 และ L5

แต่จุดลากรองจ์ไม่ได้มีอยู่แค่บนเส้นตรงเท่านั้น เพียงแต่ว่ามันยากที่จะแก้สมการเวกเตอร์เพื่อหาจุดอื่นๆ อันที่จริงแล้วถ้าดูตามประวัติศาสตร์ จุดลากรองจ์สามจุดแรกนั้นกลับถูกค้นพบก่อนโดยออยเลอร์ในปี 1765 แล้วถัดมาอีกไม่กี่ปีลากรองจ์จึงแก้สมการหาอีกสองจุดที่เหลือได้ … ก็นับว่าเป็นโชคดีที่ออยเลอร์ไม่ได้ค้นพบครบทั้งห้าจุดและเหลือพื้นที่ให้ลากรองจ์ปรับปรุงทำงานเพิ่ม ไม่งั้นโลกคณิตศาสตร์คงมีของที่ห้อยชื่อออยเลอร์เพิ่มขึ้นอีกหนึ่งชิ้นให้เราๆ สับสนจนเรียกถูกเรียกผิดเล่น 🤪

และถึงแม้ว่าการคำนวณตำแหน่งสองจุดนี้จะยุ่งยากกว่าสามจุดแรก แต่ข้อดีก็คือคราวนี้เราจะได้ตำแหน่งที่แม่นยำสวยงาม ไม่ใช่แค่ค่าประมาณที่มีข้อจำกัดด้านสัดส่วนมวลเหมือนที่ผ่านมา

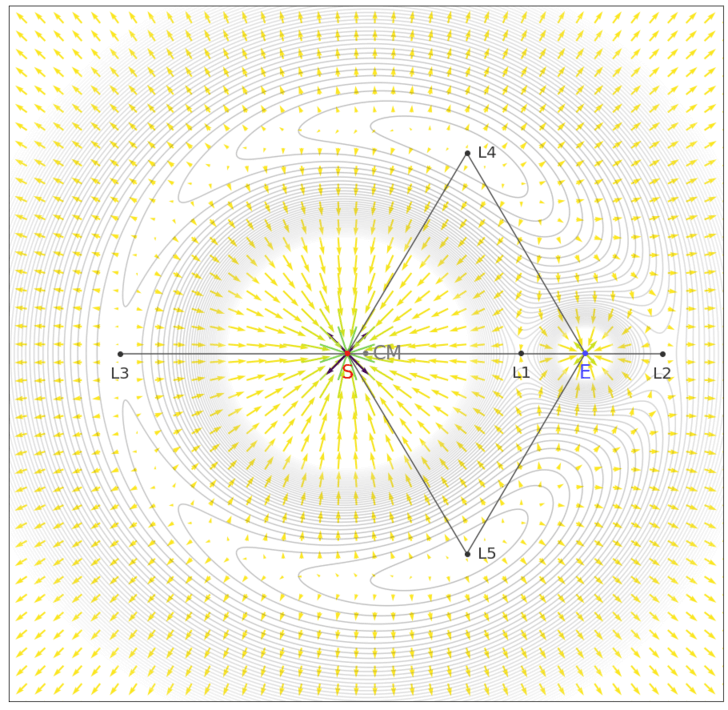
จุดลากรองจ์ทั้งห้า คราวนี้พล็อตคอนทัวร์ด้วยพลังงานศักย์ $U \propto \frac{m_\odot}{r_{\odot\varepsilon}} + \frac{m_\oplus}{r_{\oplus\varepsilon}} + \frac{(m_\odot+m_\oplus)r^2}{2r_{\odot\oplus}^3}$

สำหรับการคำนวณสองจุดที่เหลือ เราจะเริ่มจากการกลับไปวางพื้นฐานนิยามเวกเตอร์ต่างๆ อย่างรัดกุมก่อน ให้จุดศูนย์กลางมวลเป็นจุดหมุนของระบบที่ตำแหน่ง $\left[\begin{smallmatrix}0 \newline 0\end{smallmatrix}\right]$ เราจะนำดวงอาทิตย์และโลกไปวางไว้ยังตำแหน่ง $\vec{r}_o = \left[\begin{smallmatrix}x_o \newline 0\end{smallmatrix}\right]$ สำหรับ $o\in\lbrace\odot,\oplus\rbrace$ ที่สอดคล้องกับสมการนี้เพื่อให้จุดศูนย์กลางมวลอยู่ ณ จุดกำเนิด

\[\begin{equation} m_\odot x_\odot + m_\oplus x_\oplus = 0 \label{eq:center-of-mass}\tag{2} \end{equation}\]

ให้ตำแหน่งต่างๆ ที่เราสนใจเขียนแทนด้วยเวกเตอร์ $\vec{r}=\left[\begin{smallmatrix}x \newline y\end{smallmatrix}\right]$ ดังนั้นจะได้ว่าระยะห่างระหว่างตำแหน่งที่สนใจไปยังเทหวัตถุแต่ละชิ้นคือ $r_o=\abs{\vec{r}-\vec{r}_o}$

เมื่อต้องการเขียนสมการขนาดแรงโน้มถ่วงให้อยู่ในรูปเวกเตอร์ จะมีพจน์ที่เป็นเวกเตอร์หน่วยชี้เข้าหาเทหวัตถุติดเพิ่มเข้ามา ดังนั้นสมการจึงกลายเป็น

\[\vec{F}_o = \frac{Gm_om_\varepsilon}{\abs{\vec{r}_o-\vec{r}}^2} \frac{(\vec{r}_o-\vec{r})}{\abs{\vec{r}_o-\vec{r}}}\]

ส่วนสมการขนาดแรงเหวี่ยงหนีศูนย์กลางนั้นมีขนาดของทิศทาง $r$ บ่งไว้อยู่แล้ว จึงแปลงเป็นเวกเตอร์ได้เลย

\[\vec{F}_c = \frac{G(m_\odot+m_\oplus)m_\varepsilon\vec{r}}{r_{\odot\oplus}^3}\]

ดังนั้นผลรวมแรงจากสมการ $\eqref{eq:zero-force}$ จึงสามารถเขียนในรูปเวกเตอร์ของ $\vec{r}$ ได้ว่า

\[\frac{m_\odot}{r_{\odot\varepsilon}^3} (\vec{r}_\odot{-}\vec{r}) + \frac{m_\oplus}{r_{\oplus\varepsilon}^3} (\vec{r}_\oplus{-}\vec{r}) + \frac{(m_\odot{+}m_\oplus)}{r_{\odot\oplus}^3} \vec{r} = 0\]

โอเค หน้าตาสมการสวยดี และถ้าพยายามถึกแก้สมการไปก็อาจจะพบคำตอบ แต่ตัวเลขทื่อๆ ที่ได้มาอาจทำให้เราพลาดความเข้าใจเบื้องลึกเบื้องหลังไป เราจะใช้เทคนิคเปลี่ยนฐานปริภูมิเข้าช่วย โดยเลือกให้แกนหนึ่งนั้นขนานกับ $\vec{r}$ ส่วนอีกแกนก็ตั้งฉากไปเลย ซึ่งหนึ่งในวิธีที่ทำได้โดยง่ายก็คือ

\[\hat{u} = \begin{bmatrix}x \\ y\end{bmatrix} \quad\quad\text{and}\quad\quad \hat{v} = \begin{bmatrix}-y \\ x\end{bmatrix}\]

การจะเขียนเวกเตอร์ $a\hat\imath+b\hat\jmath$ ให้อยู่ในรูป $c\hat{u}+d\hat{v}$ นั้นทำได้โดยนำอินเวอร์สของเมทริกซ์ฐานปริภูมิไปคูณกับเวกเตอร์ต้นทาง ดังนี้

\[\frac1{r^2}\begin{bmatrix} x & y \\ -y & x \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} = \begin{bmatrix} c \\ d \end{bmatrix}\]

ข้อดีของการเลือกแปลงฐานเช่นนี้ คือ แรงเหวี่ยงหนีศูนย์กลางจะปรากฏแค่บนแกน $\hat{u}$ ทำให้ที่แกน $\hat{v}$ เหลือเพียงแรงโน้มถ่วงจากสองเทหวัตถุเท่านั้น ซึ่งจะเห็นได้จาก

\[\begin{array}{rcccrcr} \vec{r}_\odot{-}\vec{r} &=& \begin{bmatrix}x_\odot{-}x \\ -y\end{bmatrix} &=& \left(\dfrac{xx_\odot}{r^2}-1\right)\hat{u} &-& \dfrac{yx_\odot}{r^2}\hat{v} \\ \vec{r}_\oplus{-}\vec{r} &=& \begin{bmatrix}x_\oplus{-}x \\ -y\end{bmatrix} &=& \left(\dfrac{xx_\oplus}{r^2}-1\right)\hat{u} &-& \dfrac{yx_\oplus}{r^2}\hat{v} \\ \vec{r} &=& \begin{bmatrix}x \\ y\end{bmatrix} &=& 1\;\hat{u} &+& 0\;\hat{v} \end{array}\]

ดังนั้นขนาดของแรงที่เหลืออยู่ตามแนวแกน $\hat{v}$ จึงแปรผันกับ

\[F_\perp \propto \frac{m_\odot}{r_{\odot\varepsilon}^3} \frac{yx_\odot}{r^2} + \frac{m_\oplus}{r_{\oplus\varepsilon}^3} \frac{yx_\oplus}{r^2}\]

เราต้องการจุดที่หยุดนิ่งเทียบกับระบบ นั่นก็คือ $F_\perp = 0$ จึงทำให้สมการข้างต้นลดรูปเหลือ

\[0 = \frac{m_\odot x_\odot}{r_{\odot\varepsilon}^3} + \frac{m_\oplus x_\oplus}{r_{\oplus\varepsilon}^3}\]

ระลึกถึงข้อจำกัดของสมการจุดศูนย์กลางมวล $\eqref{eq:center-of-mass}$ ดังนั้นจะได้ว่า $r_{\odot\varepsilon}=r_{\oplus\varepsilon}$ หรือก็คือจากจุดที่เสถียรไปยังดวงอาทิตย์และโลกนั้นต้องมีระยะห่างเท่ากัน เพื่อความสะดวก ต่อไปนี้จะเขียนแทนระยะทางดังกล่าวด้วย $r_\wedge$

ย้อนกลับมาดูขนาดของแรงในแนวแกน $\hat{u}$ ซึ่งเป็นแกนที่ขนานไปกับ $\vec{r}$ จะได้ว่า

\[F_\parallel \propto \frac{m_\odot}{r_{\odot\varepsilon}^3} \left(\frac{xx_\odot}{r^2}-1\right) + \frac{m_\oplus}{r_{\oplus\varepsilon}^3} \left(\frac{xx_\oplus}{r^2}-1\right) + \frac{(m_\odot+m_\oplus)}{r_{\odot\oplus}^3}\]

เช่นเดิม เราสนใจกรณีที่ $F_\parallel=0$ ดังนั้น

\[\begin{align*} 0 &= \frac{m_\odot}{r_\wedge^3} \left(\frac{xx_\odot}{r^2}-1\right) + \frac{m_\oplus}{r_\wedge^3} \left(\frac{xx_\oplus}{r^2}-1\right) + \frac{(m_\odot+m_\oplus)}{r_{\odot\oplus}^3} \\ &= \left( \frac{m_\odot+m_\oplus}{r_{\odot\oplus}^3} - \frac{m_\odot+m_\oplus}{r_\wedge^3} \right) + \frac{x}{r^2r_\wedge^3} (m_\oplus x_\oplus + m_\odot x_\odot) \end{align*}\]

จะเห็นว่าพจน์หลังนั้นกลับมาเข้าข้อจำกัดของ $\eqref{eq:center-of-mass}$ อีกครั้ง ถึงตรงนี้เราก็จะเหลือแค่

\[0 = \frac{m_\odot+m_\oplus}{r_{\odot\oplus}^3} - \frac{m_\odot+m_\oplus}{r_\wedge^3}\]

ซึ่งก็คือ $r_\wedge = r_{\odot\oplus} = r_{\odot\varepsilon} = r_{\oplus\varepsilon}$ หรือตีความได้ว่าจุดลากรองจ์แต่ละจุดที่เหลือนี้ จะต้องอยู่บนยอดหนึ่งของรูปสามเหลี่ยมด้านเท่าที่จุดยอดอื่นๆ คือดวงอาทิตย์กับโลกนั่นเอง!

สมบัติสำคัญของ L4 กับ L5 คือการเป็นจุดเสถียร แม้จากพล็อตพลังงานศักย์จะบอกว่ามันอยู่บนยอดเขาก็ตาม แต่เพราะเมื่อวัตถุเคลื่อนที่ออกห่างจุดนี้แล้วแรงคอริออลิสจะคอยผลักมันกลับเข้าไปวนเวียนอยู่ในบริเวณดังกล่าว ต่างจากจุด L1 L2 L3 ที่อยู่บนอานม้าที่พร้อมจะไหลเข้าไปหาดวงอาทิตย์หรือโลกได้ง่ายๆ ดาวเทียมบนจุดอานม้าจึงต้องคอยเผาเชื้อเพลงเพื่อปรับเส้นทางเป็นระยะๆ นั่นเอง

สำหรับระบบดวงอาทิตย์-โลก จุดลากรองจ์ที่อยู่บนยอดสามเหลี่ยมอาจส่งผลไม่ชัดเท่าไหร่ อาจเพราะมวลที่แตกต่างกันมากๆ จนจุดศูนย์กลางมวลกับจุดศูนย์กลางดวงอาทิตย์แทบจะเป็นจุดเดียวกัน แต่หากไปมองคู่ดวงอาทิตย์-ดาวพฤหัสแล้วจะเห็นว่าจุดนี้มีบทบาทเด่นชัดในธรรมชาติ ซึ่งเป็นบริเวณที่เราจะพบดาวเคราะห์น้อยโคจรอยู่ก่อนหน้าหรือตามหลังดาวพฤหัสในมุม $60^\circ$ เป็นจำนวนมาก … มากเสียจนเอาชื่อทหารในสงครามกรุงทรอยมาตั้งก็ยังไม่พอเลยหละ 😅

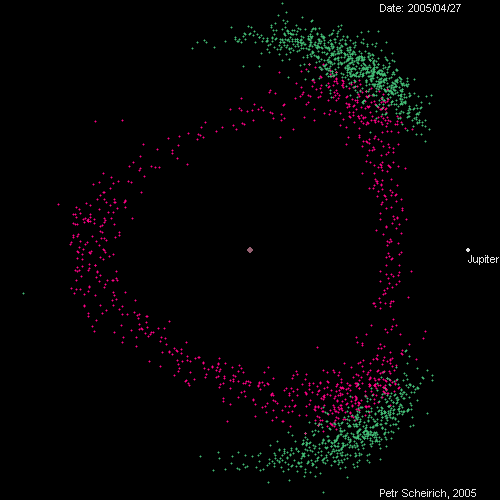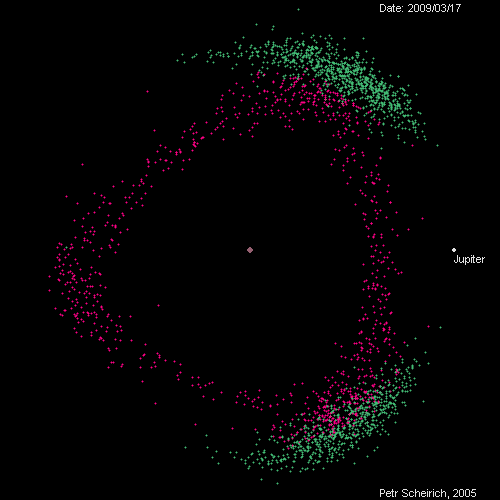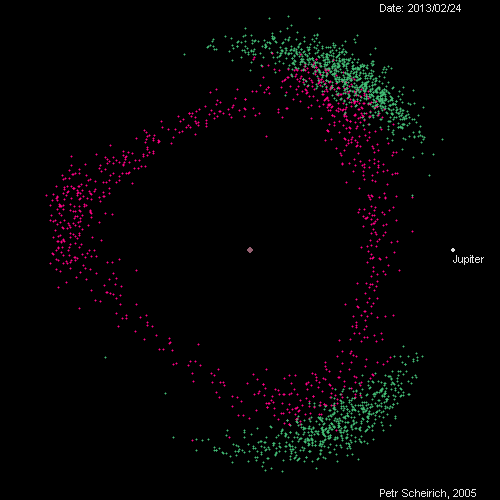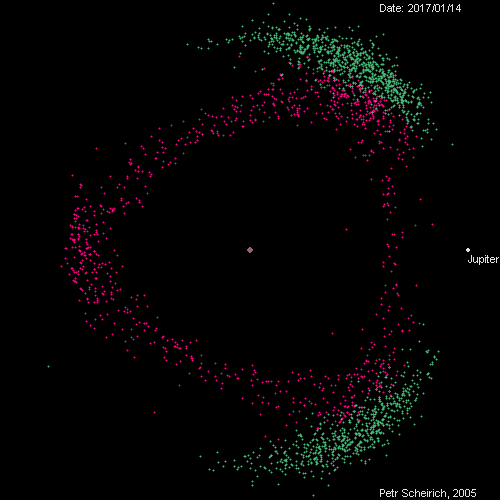
ดาวเคราะห์น้อยรอบดาวพฤหัส ซึ่งกระจุกตัวตามจุดลากรองจ์ต่างๆ – ภาพจาก Petr Scheirich ผ่าน leancrew.com

ก็น่าสนใจว่าในความว่างเปล่ามืดมิดไร้ซึ่งสิ่งใด บางครั้งมันก็ไม่ได้ไร้ซึ่งความสำคัญไปเสียทีเดียว อย่างเช่นการเป็นจุดสมดุลแห่งพลังทั้งหลายแบบจุดลากรองจ์เหล่านี้

อ้างอิง

• NASA: ‘L2’ Will be the James Webb Space Telescope’s Home in Space
• Scott Manley: What Makes Lagrange Points Special Locations In Space
• Neil J. Cornish: The Lagrange Points
• Dennis Westra: Lagrangian Points
• 3Blue1Brown: Change of basis