Solve Wordle in 3.7 Guesses 🤪
Wordle is a viral game created by @powerlanguish. It’s a scrabble version of the classic Mastermind; however, alphabets are used instead of colored pegs. The objective of the game is to find a five-letter word within minimum guesses as possible. Each guess will hint us whether any letter is in the right place, misplaced, or out of place. It gives us at most six guesses before spelling OWARI. Which is quite generous, because on average, we can solve it within 3.7 guesses1 if we play optimally.2
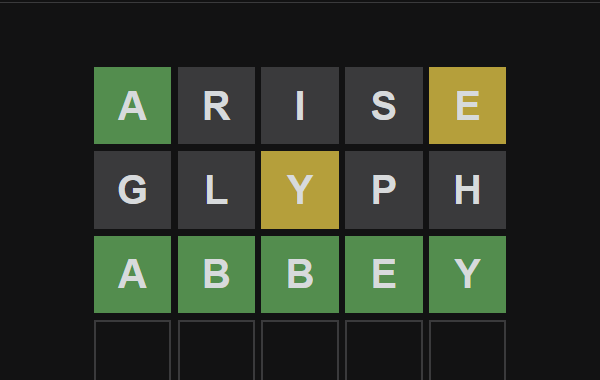
Puzzle #208, 2022-Jan-13
But how to solve the puzzle systematically? Maybe math have an answer for it.
The First Guess
There are around 2.3k distinct solutions in the game (precise word list may be obtained via game’s JavaScript). We want to locate the right one fast, so a guess that can reject lots of feasible solutions is ideal.
If cryptography teach us something, E is the most common letter in English. Which is also true within the game’s dictionary, because it appear almost half of all time. So if we guess a word that’s contain a letter E, we can reject half of the feasible solutions whether E is in the final solution or not.
Then why satisfy with the only letter E, when we can guess a word with five letters? Rank common letters from the word list, we find these ten letters in order EAROTLISNU. Too bad that we can’t input a gibberish word with the first five, so we have to make it LATER.
The word LATER might looks nice since it only skip O, thus can reject many feasible solutions. However, the rejection power of this word is weakened by the fact that TE is one of the most common bigram. Heck, bigram only concern consecutive letters, but for this game a pair of frequent letters can be placed anywhere in the word to take effect. And with only TE it reduce the power of E by $25\%$ already!
Luckily, trigram help strengthen some power back, since we will subtract more than we have to when considering bigram over individual letter. However, four-gram weaken it again, and five-gram try to come back to save the day. In general, each layer either strengthen or weaken the power of the previous $n$-gram layer. This is the inclusion-exclusion principle, which counts the size of interested portion of a set. It can be illustrated nicely (and universally) with the Venn diagram.
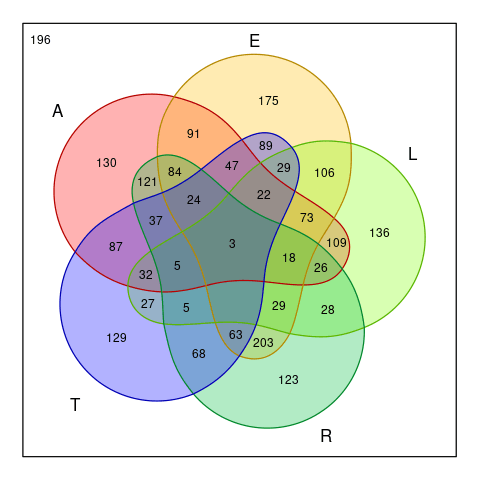
Size of feasible solutions after we guess with the word
LATER
In the above diagram, there are five main (wobbly) circles. Each circle shows how many feasible solutions remain if a guess letter is correct. Region of overlapping circles indicated the case where multiple guess letters are correct at the same time. Surprisingly, the core of the diagram, where all five letters are correct, is not equal to one. Since there are three words with the same set of letters: ALERT, ALTER, and LATER.
Observe a region of size $203$ on the lower center of the diagram. This one required ER, but not ALT to appear in the final solution. It is the largest region, meaning that if we landing on this portion, we have a large number of words to drill down later.
On the other hand, there is a region with zero elements in it. Namely, the region that required ELRT, but not A. It’s kinda wasted that these five letters leaves the region empty.
So the word LATER might not be a good candidate after all. We want to guess with a word that partition the diagram into $2^5=32$ non-empty regions. Also the largest region should be as small as possible to worked on easily. Thus,ARISE met the requirement perfectly.
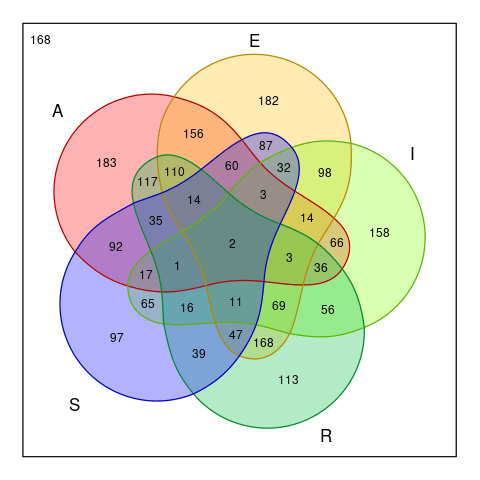
Size of feasible solutions after we guess with the word
ARISE
Note that this analyses doesn’t take the position of the letters into account, the actual feasible solutions might be a lot smaller than this.
The Second Guess
If we are lucky, the first guess will returns some green (right place) or yellow (misplaced). Don’t use them to build the second guess. We don’t wanna go slow by inputting partial correct answers and let them eats up our space for getting feedback. Instead, we will prune the feasible solutions furthermore with the whole new set of letters.3
Suppose the first guess is ARISE, which result A in the right place, E misplaced, and other letters just plain wrong. We may the prune feasible solutions by testing against these three regular expressions:
/^a[^ris]{4}$/
/^....[^e]$/
/e/
Although the diagram tells us that there are as much as $156$ feasible solutions. The actual result after aggressive pruning result in only $10$ solutions. All of them starts with an A and have a letter E somewhere, but not at the end.
abbey abled adept agent ahead
alley amend angel annex apnea
Within this smaller feasible solutions, a new frequency signature emerge. Ignoring AE, we see that ND each appear around half. Follow closely by LGBTPY. We want make a guess that prune these letters fast. It’ll be too slow to take specimen from this already small sets.
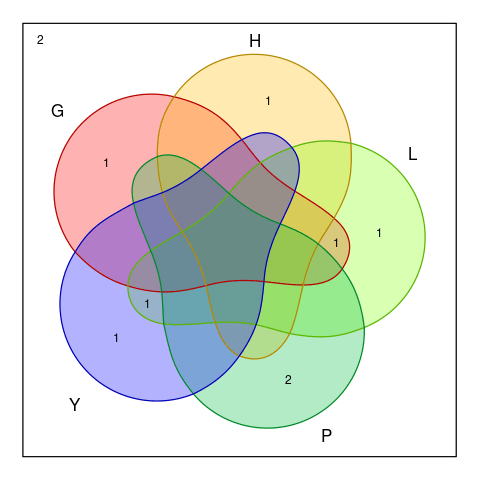
For now, we take a step back and look at the whole word list. Pick a word that can break apart these feasible solutions into lots of smaller regions. Again, we found the perfect candidate for the second guess: GLYPH.
Size of feasible solutions after feedback
A...eand try to guess withGLYPH
That’s mean if we get P or nothing, then we have to guess at most two more time. Otherwise we can pinpoint the final solution right away.
If we’re unlucky that this guess doesn’t gives enough clue to solve the puzzle, just redo this process of second guess again. Be mindful that we might run out of alphabets and have to reuse vowels. Also, at some point, trying the only available guess within feasible solutions became better idea. No matter what, we’ll arrived at the final solution eventually.
It’s not Perfect, but Good Enough
This is just a rough concept that can be automate somewhat reliably. The stats are:
| Guesses | Frequency | Histogram 🤪 |
|---|---|---|
| 1 | 1 | █ |
| 2 | 26 | █ |
| 3 | 1106 | ████████████████████████████ |
| 4 | 703 | ██████████████████ |
| 5 | 455 | ████████████ |
| 6 | 23 | █ |
| 7 | 1 | █ |
With the only failure:
arise 🢡 moldy 🢡 gaunt 🢡 whoop 🢡 batch 🢡 hatch 🢡 catch
Which can be solve manually. Or by sacrificing some statistics, we may contain the number of guesses to fit within the available quota.
Python Code
import re
from enum import IntEnum
from itertools import combinations
from collections import Counter, defaultdict
WORDS = open('wordlist-solution.txt').read().split()
class Position(IntEnum):
RIGHT = 0
MISS = 1
WRONG = 2
class AutoReplyWordleAdapter(object):
def __init__(self, answer):
self.answer = answer
def __call__(self, word):
out = []
for a, w in zip(self.answer, word):
if a == w:
out += [Position.RIGHT]
elif w in self.answer:
out += [Position.MISS]
else:
out += [Position.WRONG]
return out
class ManualReplyWordleAdapter(object):
def __call__(self, word):
print('The program guess:', word)
while True:
result = input('Please response 5 chars [RMW]: ').strip().lower()
if len(result) == 5 and set(result).issubset(set('rmw')):
break
return [Position('rmw'.index(c)) for c in result]
def inclusion_exclusion(elements):
for how_many in range(1+len(elements)):
for selected in combinations(elements, how_many):
yield selected
def frequency_table(words, ignore=set()):
freq = defaultdict(int)
for word in words:
alphabets = ''.join(sorted(set(word) - ignore))
for selected in inclusion_exclusion(alphabets):
freq[selected] += 1
return freq
def partition(word, freq):
alphabets = sorted(set(word))
parts = defaultdict(int)
for base in inclusion_exclusion(alphabets):
remainings = set(alphabets) - set(base)
for selected in inclusion_exclusion(remainings):
parity = [-1, 1][len(selected) % 2 == 0]
find = tuple(sorted(set(selected) | set(base)))
parts[base] += parity * freq[find]
return {key: value for key, value in parts.items() if value}
def partition_comparator(freq):
def aux(word):
parts = partition(word, freq)
return len(parts.values()), -max(parts.values())
return aux
class Solver(object):
def __init__(self, wordle):
self.wordle = wordle
self.local_accepts = [None for _ in range(5)]
self.local_rejects = [set() for _ in range(5)]
self.global_accepts = set()
self.global_rejects = set()
self.attempts = []
def run(self):
words = WORDS
while None in self.local_accepts:
guess = self.select_phase(words)
self.attempts += [guess]
self.update_wordle_feedback(guess)
words = self.filtering(words)
return self.attempts
def make_regex_filter(self):
pattern = '^'
for i in range(5):
if self.local_accepts[i]:
pattern += self.local_accepts[i]
elif self.global_rejects or self.local_rejects[i]:
rejects = ( ''.join(self.local_rejects[i])
+ ''.join(self.global_rejects) )
pattern += f'[^{rejects}]'
else:
pattern += '.'
pattern += '$'
return re.compile(pattern)
def ignore_alphabets(self):
return ( set(a for a in self.local_accepts if a)
| self.global_accepts | self.global_rejects )
def ignore_consonants(self):
return self.ignore_alphabets() - set('aeiou')
def select_phase(self, words):
if len(words) == 1:
return words[0]
if len(self.attempts) < 2:
return self.phase1(words)
elif len(self.attempts) < 3:
return self.phase2(words)
elif len(self.attempts) < 4:
return self.phase3(words)
return self.phase2(words)
def phase1(self, words):
freq = frequency_table(words, self.ignore_alphabets())
candidates = filter(self.ignore_alphabets().isdisjoint, WORDS)
guess = max(candidates, key=partition_comparator(freq))
if self.attempts and self.attempts[-1] == guess:
guess = max(words, key=partition_comparator(freq))
return guess
def phase2(self, words):
freq = frequency_table(words, self.ignore_alphabets())
return max(words, key=partition_comparator(freq))
def phase3(self, words):
freq = frequency_table(words, self.ignore_alphabets())
candidates = list(filter(self.ignore_consonants().isdisjoint, WORDS))
if candidates:
return max(candidates, key=partition_comparator(freq))
return max(words, key=partition_comparator(freq))
def update_wordle_feedback(self, guess):
feedback = self.wordle(guess)
for i, (alphabet, hint) in enumerate(zip(guess, feedback)):
if hint == Position.RIGHT:
self.local_accepts[i] = alphabet
if hint == Position.MISS:
self.local_rejects[i] |= {alphabet}
self.global_accepts |= {alphabet}
if hint == Position.WRONG:
self.global_rejects |= {alphabet}
def filtering(self, words):
match = self.make_regex_filter().match
return list(filter(self.global_accepts.issubset, filter(match, words)))
# ============================================================================
import multiprocessing
def process(word):
output = Solver(AutoReplyWordleAdapter(word)).run()
print(word, ' '.join(output), flush=True)
return output
pool = multiprocessing.Pool(16)
tests = list(pool.map(process, WORDS))
Related Works

author