ก่อนเริ่มแข่งเมื่อวานคิดว่ายังไงก็ผ่านฉลุยได้เข้ารอบถัดไปแน่ๆ แต่เหมือนยิ่งการแข่งปีหลังๆ ยิ่งมีขาโหดหน้าใหม่งอกขึ้นมาเรื่อยๆ พอเห็นผลคะแนนหลังแข่งจบนี่เข้าใจเลยว่ายังไงก็ต้องเก็บคะแนนเต็มเท่านั้นถึงจะการันตีผ่านเข้ารอบ

แน่นอนว่ารอบนี้ไม่เต็มเพราะข้อสุดท้ายนั้นยากจัด 5555TT55 ส่วนข้อแรกก็ง่ายเกินไปแบบว่าน่าจะเอาไว้ปลอบใจให้มีคะแนนติดไม้ติดมือกลับไปบ้าง ก็เหลือแต่ข้อตรงกลางที่ยากพอดีๆ นี่แหละ

จริงๆ ชื่อโจทย์ภาษาอังกฤษนี่แอบฮา(ไม่ออก)อยู่ เพราะเล่นกับคำว่า inflation ที่แปลว่า “การเป่าลม” หรือ “เงินเฟ้อ” ก็ได้ ซึ่งน่าจะล้อกับสถานการณ์ปัจจุบันที่ทั่วโลกเผชิญวิกฤติเศรษฐกิจนี้กันถ้วนหน้า ([1], [2], [3]) จนทำให้คนรุ่นก่อร่างสร้างตัวจำนวนมากเลือกที่จะยอมแพ้ในระบบทุนนิยมแล้วแค่ใช้ชีวิตไปวันๆ ปล่อยให้อนาคตเป็นเรื่องในอนาคตไม่เก็บมาคิดใส่ใจกันเลยทีเดียว ([4], [5], [6])

แต่โอเคแหละ โจทย์ไม่ได้เอาเรื่องจริงมาเขียนเป็นโจทย์ให้เราอ่านแล้วหดหู่เล่น เพราะเปลี่ยนไปเล่าเรื่องผ่านร้านรับเติมลมแห่งหนึ่งที่มีลูกค้าต่อคิวกันเยอะมาก จนต้องหาวิธีจัดลำดับการเติมลมสิ่งของต่างๆ ของลูกค้าแต่ละคนให้เกิดประสิทธิภาพสูงสุด ในขณะที่รักษาสิทธิลูกค้าแต่ละคนโดยไม่ให้ลัดคิวกัน

เล่าให้ละเอียดก็คือ ร้านมีเครื่องเติมลมอัตโนมัติที่มีปุ่มขึ้นลงไว้ปรับให้ได้แรงดันลมที่ต้องการ ตอนเปิดร้านเครื่องดังกล่าวถูกตั้งแรงดันไว้เป็นศูนย์ มีลูกค้าต่อคิวกันอยู่ $n<1000$ คน แต่ละคนมีสิ่งของทีต้องการจะเติมลมเท่ากันที่ $p<100$ ชิ้น ให้หาว่าพนักงานร้านต้องกดปุ่มปรับแรงดันลมเป็นจำนวนรวมน้อยที่สุดกี่ครั้งเมื่อบริการลูกค้าจนครบทุกคน โดยไม่สลับตำแหน่งการมาก่อนหรือหลังของลูกค้า แต่สามารถสลับสิ่งของที่ลูกค้าแต่ละคนนำมาเติมลมได้

สังเกตว่าสำหรับลูกค้าหนึ่งคน เราสามารถสลับสิ่งของที่ต้องการเติมลมอย่างไรก็ได้ เพราะฉะนั้นจุดที่ทิ้งปัญหาให้เรามาขบคิดเพื่อกดปุ่มเพียงน้อยครั้ง จะเป็นช่วงรอยต่อระหว่างการให้บริการลูกค้านั่นเอง

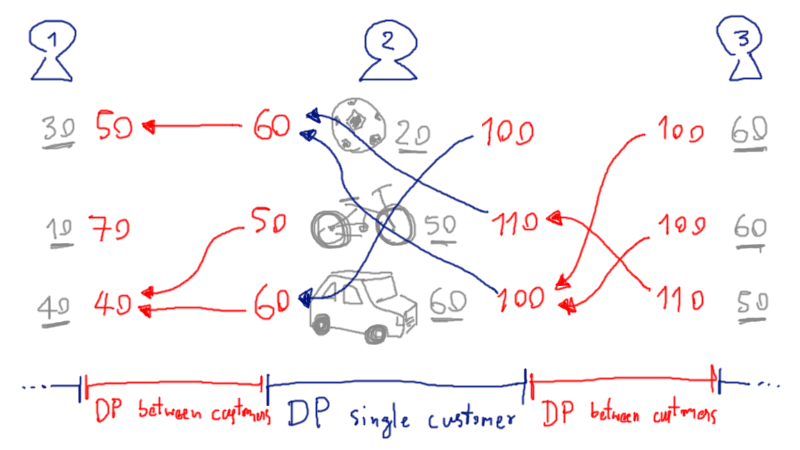
ลองนึกตัวอย่างที่ลูกค้าคนแรกมีของสองชิ้นที่ต้องการแรงดัน $\lbrace20,50,60\rbrace$ ปาสคาล ส่วนลูกค้าคนถัดมาต้องการแรงดัน $\lbrace50,60\rbrace$ ปาสคาล ถ้าเราปิดจ๊อปลูกค้าคนแรกที่แรงดัน $20$ ปาสคาลนั้นไม่ดีแน่ เพราะเราต้องกดปุ่มปรับแรงดันอย่างน้อยสามสิบครั้งเพื่อที่จะเริ่มให้บริการลูกค้าคนถัดไปได้ แต่ถ้าเราปิดจ๊อปลูกค้าคนแรกที่ $50$ ปาสคาลแทน เราก็จะให้บริการลูกค้าคนถัดไปได้ทันทีเลย

เนื่องจากเราต้องการคำตอบที่ดีที่สุดเมื่อให้บริการลูกค้าครบทุกคน แต่มันมีจำนวนวิธีมากเกินไปที่เราจะทดลองปิดจ๊อปทุกรูปแบบสำหรับทุกคนพร้อมกัน อย่างไรก็ตาม สังเกตว่าถ้าเราทดลองปิดจ๊อปทุกรูปแบบแต่ไล่ทำทีละคน เราก็ยังสามารถสร้างคำตอบของลูกค้าคนใหม่ต่อยอดขึ้นมาได้อยู่ ดังนั้นโครงร่างการออกแบบอัลกอริทึมของเราจะเป็นไปในแนวทางกำหนดการพลวัตร

ทั้งนี้อย่าลืมว่าสำหรับในลูกค้าหนึ่งคน เราก็ต้องเติมลมให้กับของทุกชิ้นด้วย ซึ่งก็คือจากของชิ้นแรกที่เติมลมกับของชิ้นสุดท้ายที่จะปิดจ๊อปแล้วไปรับงานลูกค้าคนใหม่ ระหว่างทางนั้นเราก็ต้องกดปุ่มปรับแรงดันเพื่อไปเติมลมให้กับของชิ้นที่ต้องการแรงดันสูงสุดและต่ำสุดอีกด้วย

ซึ่งนี่น่าจะเป็นความสวยงามของโจทย์ข้อนี้ที่ให้เราทำกำหนดการพลวัตรสองแบบล้อกันไปโดยจัดวางสับหว่างฟันปลานี่แหละ

เรายังมีข้อสังเกตที่สำคัญอีกอย่างคือระหว่างทางเราสามารถแอบละโมบได้อีกด้วย ซึ่งก็คือสำหรับลูกค้าแต่ละคน คำตอบที่ดีที่สุดจะต้องเริ่มจากการเติมลมให้กับสิ่งของชิ้นที่ต้องการแรงดันน้อยที่สุดหรือมากที่สุดเท่านั้น จึงทำให้เราได้โค้ดสุดท้ายนี้มา

from collections import namedtuple

Cell = namedtuple('Cell', 'presses pascal')

def make_init(pascal, cell):
    presses = cell.presses + abs(pascal-cell.pascal)
    return Cell(presses, pascal)

def min_init(dp_out, x):
    return min(make_init(x, c) for c in dp_out)

def make_target(pascal, cell, lo, hi):
    presses = cell.presses - abs(pascal-cell.pascal) + 2*abs(hi-lo)
    return Cell(presses, pascal)

def min_target(dp_in, x, lo, hi):
    return min(make_target(x, c, lo, hi) for c in dp_in)

def minimum_presses(ps):
    dp_out = [Cell(presses=0, pascal=0)]
    for person_products in ps:
        lo, *_, hi = sorted(person_products)
        dp_in = [min_init(dp_out, x) for x in [lo, hi]]
        dp_out = [min_target(dp_in, x, lo, hi) for x in [lo, hi]]
    return min(c.presses for c in dp_out)

for t in range(int(input())):
    n, _ = [int(x) for x in input().split()]
    ps = [[int(x) for x in input().split()] for _ in range(n)]
    answer = minimum_presses(ps)
    print(f'Case #{t+1}: {answer}')

neizod

author