กราฟนั้นเป็นโครงสร้างข้อมูลที่แปลก เพราะถึงแม้โครงสร้างหลักๆ ของมันจะคล้ายกับลิสต์หรือต้นไม้ กล่าวคือ มีข้อมูลประจำโหนดของตัวเอง และพอยเตอร์ที่ชี้ไปยังบรรดาโหนดเพื่อนบ้าน

data Graph t = Node { label :: String, value :: t, neighbors :: [Graph t] }

ซึ่งมันก็คงจะไม่มีปัญหาอะไรถ้ากราฟทั้งกราฟนั้นมีแค่โหนดเดียวที่ไม่ต้องชี้หาใครเลยแม้กระทั่งตัวมันเอง

Node "Khorat" (14.9494,102.3125) []

แต่กราฟที่มีเพียงโหนดเดียวก็คงจะดูเหงา และในความเป็นจริงกราฟมักมีโหนดเป็นจำนวนมาก ยิ่งไปกว่านั้นโหนดเพื่อนบ้านก็สามารถชี้ย้อนกลับมายังโหนดตั้งต้น ประหนึ่งการมูฟออนเป็นวงกลมได้อีกด้วย

Node "Chiang Mai" (18.7667,98.9625) [
  Node "Bangkok" (13.9125,100.6007) [
    Node "Chiang Mai" (18.7667,98.9625) [...]]]

อย่างเช่นโค้ดข้างต้นนี่รันไม่ออกแน่ๆ เพราะแค่จะไล่เขียนให้ครบยังทำไม่ได้เลย ทั้งที่จริงๆ แล้วเราก็มีโหนดเป็นจำนวนจำกัด แต่ทำไมถ้าเราจะสร้างข้อมูลที่มีหน้าตาแบบนี้ เรากลับต้องเขียนแตกมันออกมาเป็นอนันต์เทอมไปซะได้

ว่าไงนะ? ต้องการยุ่งกับอะไรที่เป็นอนันต์อย่างนั้นเหรอ … งั้นก็ใช้ความขี้เกียจ (lazy evaluation) ของ Haskell เข้าช่วยสิ!

bkk = Node "Bangkok" (13.9125,100.6007) [cnx,hkt,hdy,usm,uth,kkc,kbv,hgn,phs,bfv,maq,tdx]
cnx = Node "Chiang Mai" (18.7667,98.9625) [bkk,hkt,hdy,usm,utp,kbv,uth,kkc,hgn,hhq]
hkt = Node "Phuket" (8.1131,98.3167) [bkk,cnx,hdy,usm,utp,uth,kkc]
hdy = Node "Hat Yai" (6.9331,100.3928) [bkk,cnx,hkt,usm,uth,kkc]
usm = Node "Ko Samui" (9.5478,100.0622) [bkk,cnx,hkt,hdy,utp,kbv]
kkc = Node "Khon Kaen" (16.4666,102.7837) [bkk,cnx,hkt,hdy]
uth = Node "Udon Thani" (17.3864,102.7883) [bkk,cnx,hkt,hdy]
utp = Node "Pattaya" (12.6797,101.0050) [cnx,hkt,usm]
kbv = Node "Krabi" (8.1008,98.9847) [bkk,cnx,usm]
hgn = Node "Mae Hong Son" (19.3011,97.9747) [bkk,cnx]
phs = Node "Phitsanulok" (16.7731,100.2822) [bkk]
bfv = Node "Buri Ram" (15.2294,103.2511) [bkk]
maq = Node "Mae Sot" (16.6997,98.5450) [bkk]
tdx = Node "Trat" (12.2746,102.3190) [bkk]
hhq = Node "Hua Hin" (12.6361,99.9514) [cnx]
nak = Node "Khorat" (14.9494,102.3125) []

โค้ดนี้รันได้แน่นอน เพราะแม้ตัวแปรต่างๆ ที่เป็นบรรดาโหนดเพื่อนบ้าน (อย่างเช่นเพื่อนบ้านของ bkk ที่มี cnx,hkt,…) จะถูกเขียนนิยามในบรรทัดถัดๆ ไป แต่ด้วยความขี้เกียจของ Haskell จึงทำให้มันยังไม่รีบหาค่าเพื่อนบ้านเหล่านั้น ค่าต่างๆ ของเพื่อนบ้านจะถูกนำมาใส่ลิสต์ดังกล่าวเมื่อเราต้องการรู้รายละเอียดเพิ่มเติมเท่านั้น เช่น

map label $ neighbors $ hkt
-- ["Bangkok","Chiang Mai","Hat Yai","Ko Samui","Pattaya","Udon Thani","Khon Kaen"]

map label $ neighbors $ (!!4) . neighbors $ hkt
-- ["Chiang Mai","Phuket","Ko Samui"]

map label $ neighbors $ (!!1) . neighbors $ (!!4) . neighbors $ hkt
-- ["Bangkok","Chiang Mai","Hat Yai","Ko Samui","Pattaya","Udon Thani","Khon Kaen"]

ซึ่งความขี้เกียจแบบนี้มันทรงพลังมาก เพราะอย่างที่ได้เห็นไป เราได้ผลพลอยได้เป็นการยินยอมให้อ้างอิงถึงตัวแปรที่ยังไม่ถูกประกาศมาก่อนได้ ถ้าเทียบกับภาษาเพื่อนบ้านตระกูล Lisp แล้วนั้น letrec ยังยอมแค่การประกาศฟังก์ชันที่อ้างอิงฟังก์ชันอื่น (mutual recursion) เท่านั้น แต่ไม่สามารถประกาศตัวแปรที่อ้างอิงตัวแปรอื่นได้¹

เทคนิคแนวนี้ชาว Haskell เรียกกันว่าการผูกบ่วง (tying the knot) ซึ่งถึงแม้ว่ามันอาจจะทำให้เรารู้สึกแปลกหูแปลกตา (และสมองพัง) ไปซักหน่อย แต่สุดท้ายแล้วมันก็ทำงานได้

อย่างไรก็ตาม การแทรกข้อมูลลงไปในโค้ด (hard code) เพื่อสร้างกราฟตามข้างต้นนั้น เราทำได้ก็เพราะเรารู้รูปร่างหน้าตาของมันมาก่อนแล้ว แต่มันก็เป็นวิธีการเขียนโค้ดที่ไม่ค่อยดีซักเท่าไหร่ และในโลกจริงเรามักต้องรับข้อมูลกราฟเข้ามาทีหลัง หรือแม้กระทั่งเปลี่ยนแปลงค่าต่างๆ ในกราฟ อย่างเช่นพวกโจทย์เขียนโปรแกรมที่มักเริ่มด้วยการให้ $n,m$ แทนจำนวนโหนดและเส้นเชื่อม แล้วค่อยให้ข้อมูลต่างๆ ตามมาทีหลัง ประมาณนี้

16 31
13.9125 100.6007 Bangkok
18.7667 98.9625 Chiang Mai
8.1131 98.3167 Phuket
6.9331 100.3928 Hat Yai
9.5478 100.0622 Ko Samui
16.4666 102.7837 Khon Kaen
17.3864 102.7883 Udon Thani
12.6797 101.0050 Pattaya
8.1008 98.9847 Krabi
19.3011 97.9747 Mae Hong Son
16.7731 100.2822 Phitsanulok
15.2294 103.2511 Buri Ram
16.6997 98.5450 Mae Sot
12.2746 102.3190 Trat
12.6361 99.9514 Hua Hin
14.9494 102.3125 Khorat
1 2
1 3
1 4
1 5
1 7
1 6
1 9
1 10
1 11
1 12
1 13
1 14
2 3
2 4
2 5
2 8
2 9
2 7
2 6
2 10
2 15
3 4
3 5
3 8
3 7
3 6
4 5
4 7
4 6
5 8
5 9

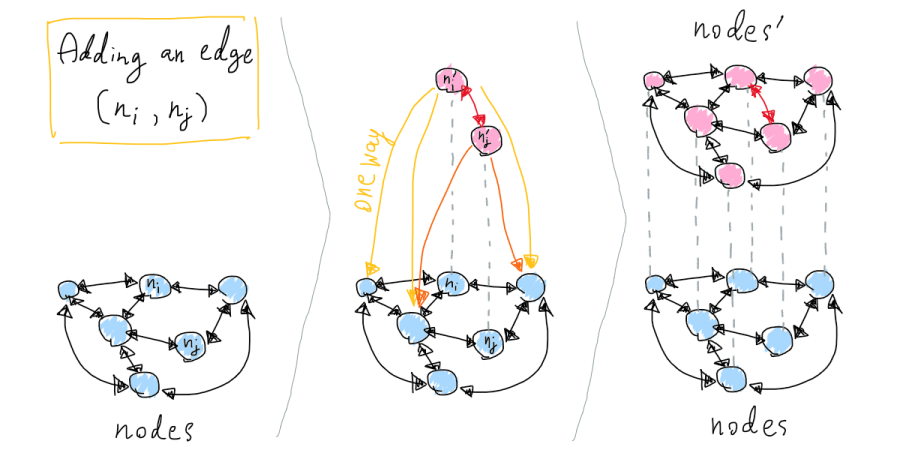
เราจะอ่านข้อมูลเหล่านี้เข้ามาเพื่อสร้างกราฟอย่างไร? อย่าลืมว่าแต่ละโหนดในกราฟนั้นชี้หาเพื่อนบ้านทั้งไปและกลับ ดังนั้นถึงแม้เราจะอัพเดทข้อมูลในโหนดเพียงหนึ่งโหนด แต่เราก็ต้องอัพเดททุกโหนดในกราฟให้ชี้กลับมาหาโหนดที่อัพเดทนี้อีกด้วย

การแก้ไขค่าในกราฟ (เพิ่มเส้นเชื่อมใหม่) ที่ต้องแก้ทุกโหนดในกราฟให้ชี้มายังโหนดที่ถูกแก้ด้วย

getWords :: IO [String]
getWords = getLine >>= return . words

getInts :: IO [Int]
getInts = getWords >>= return . map read

readAirport :: IO (Graph (Float,Float))
readAirport = getWords >>= return . makeAirport
    where makeAirport (r1:r2:ws) = Node (unwords ws) (read r1,read r2) []

readRoute :: Int -> [Graph t] -> IO [Graph t]
readRoute 0 nodes = return nodes
readRoute m nodes = getInts >>= readRoute (m-1) . connectRoute nodes

connectRoute :: [Graph t] -> [Int] -> [Graph t]
connectRoute nodes [i,j] = nodes'
    where [ni,nj] = map (nodes !!) (map pred [i,j])
          nodes'  = map alter nodes
          insert (Node l p ns) n = Node l p (n:ns)
          update (Node l p ns)   = Node l p (filter (previous ns) nodes')
          previous ns n          = elem (label n) (map label ns)
          alter n
            | label n == label ni = update (insert ni (alter nj))
            | label n == label nj = update (insert nj (alter ni))
            | otherwise           = update n

main :: IO ()
main = do
    [n,m] <- getInts
    nodes <- replicateM n readAirport >>= readRoute m

นั่นก็คือใน Haskell การอัพเดทข้อมูลแต่ละทีจะกินเวลาเป็น $O(n+m)$ เลยทีเดียว ทั้งที่ถ้าเอาไปเขียนในภาษาโปรแกรมเชิงคำสั่งอย่าง C++ หรือ Python แล้ว การอัพเดทกราฟมันก็แค่ $O(1)$ เท่านั้นเอง

แน่นอนว่านี่จะทำให้เกิดปัญหาตามมาอย่างมากมาย อย่างเช่นเวลาท่องลงไปในกราฟที่เราต้องการจดจำว่าเคยเห็นโหนดไหนมาแล้วบ้าง (เพื่อป้องกันไม่ให้เราติดลูปในการท่องกราฟ) เนื่องจากเราต้องการเลี่ยงการอัพเดทที่กินเวลามหาศาล เราอาจเปลี่ยนไปเก็บข้อมูลว่าเคยเยี่ยมโหนดไหนไปแล้วบ้างลงต้นไม้ค้นหาซักแบบที่ใช้เวลาแนว $O(\log n)$ แล้วก็ส่งต่อข้อมูลนี้แค่ตอนในสโคปของอัลกอริทึมก็ได้ (โค้ดด้านล่างนี้ไม่ได้ห่วงเรื่องประสิทธิภาพมากนัก และใช้แค่ลิสต์ธรรมดาเก็บว่าเคยไปเยี่ยมโหนดไหนแล้วบ้าง)

hav  = (**2) . sin . (/2)
ahav = (2*) . asin . sqrt
sphericalDistance [p1,p2,l1,l2] =
    ahav (hav (p2-p1) + (1 - hav (p2-p1) - hav (p2+p1)) * hav (l2-l1))
distanceOnEarth (Node _ (lat1,long1) _) (Node _ (lat2,long2) _) =
    6371 * sphericalDistance (map (*(pi/180)) [lat1,lat2,long1,long2])

allPaths ps s t
  | label s == label t = [t:ps]
  | otherwise          = concat $ map (allPaths (t:ps) s) $ unvisited t
        where previous n = elem (label n) (map label ps)
              unvisited  = filter (not . previous) . neighbors

shortestPath s t = minimum [(dist ps, map label ps) | ps <- allPaths [] s t]
    where dist ps = sum [distanceOnEarth s t | (s,t) <- zip ps (tail ps)]


----------------------------------------------------------------------------

shortestPath hgn kkc
-- (598.5705261061864,["Mae Hong Son","Chiang Mai","Khon Kaen"])

shortestPath phs utp
-- (1171.8935136659995,["Phitsanulok","Bangkok","Ko Samui","Pattaya"])

… แบบนี้แล้วการเขียนโปรแกรมเชิงฟังก์ชันก็คงไม่ค่อยเหมาะกับการจัดการกราฟเท่าไหร่หละมั้ง? หรือไม่งั้นก็ต้องใช้ท่าอื่นๆ เช่นนิยามกราฟผ่าน $G=(V,E)$ ที่มองโหนดกับเส้นเชื่อมเป็นชุดข้อมูลที่แยกกันไปเลย จะได้เลี่ยงประเด็นเรื่องการอัพเดทข้อมูลที่ต้องวนลึกลงไปเหมือนงูกินหางแบบนี้อีกด้วย

อ้างอิง

• Stack Overflow - How do you represent a graph in Haskell?
• HaskellWiki - Tying the Knot

neizod

author