ถ้าใครได้รับสมการคณิตศาสตร์หน้าตาประหลาดๆ ตัวนี้ ก็อย่าเพิ่งตกอกตกใจประหนึ่งต้องเวียนกลับไปติดอยู่ในฝันร้าย แค่ลองโยนให้เครื่องคิดเลข¹พล็อตดู จะพบกับผลลัพธ์หน้าตาสวยงามเช่นนี้ …

พล็อตสมการ $(x^2+y^2-1)^3 - x^2y^3 = 0$ บนระบบพิกัดคาร์ทีเซียน

สำหรับหลายคนแค่นี้ก็น่าจะพอแล้ว แต่ถ้าใครอยากจะลองแกะดูว่าสมการนี้ทำงานยังไง แม้ดูเผินๆ แล้วมันออกจะซับซ้อนไปซักหน่อย (และน่าจะเกินความรู้ภาคบังคับไปบ้าง) แต่เราอาจเริ่มจากจัดรูปมันก่อนก็ได้

\[\begin{align} (x^2 + y^2 -1)^3 &= x^2y^3 \\ x^2 + y^2 -1 &= x^{2/3}y \\ y^2 - x^{2/3}y + (x^2{-}1) &= 0 \end{align}\]

จะเห็นว่าจริงๆ แล้วมันก็แค่สมการกำลังสองบนตัวแปร $y$ นั่นจึงทำให้เราได้

\[y = \frac{x^{2/3} \pm \sqrt{x^{4/3} - 4(x^2{-}1)}}2\]

โอเค หน้าตาน่าเกลียดยิ่งกว่าเดิมอีก 55555555

แต่ถ้ากลั้นใจดูต่ออีกหน่อย จะเห็นว่าเราอาจแยกผลลัพธ์กำลังสองได้ออกเป็นสองส่วน คือ

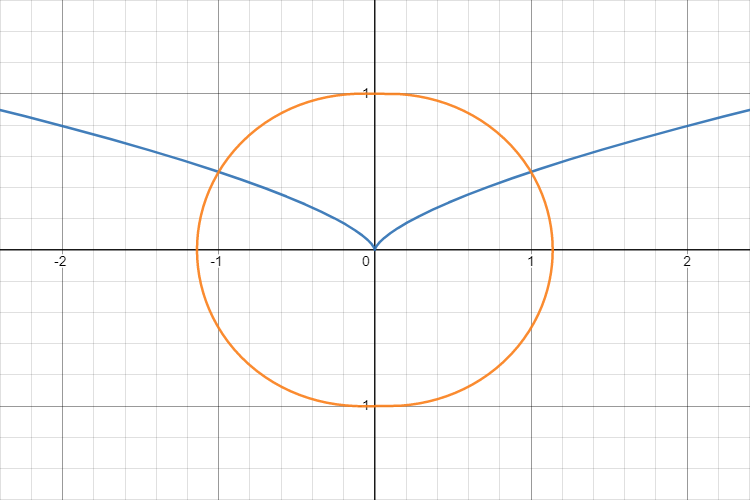
\[\begin{align} y &= f(x) + g(x) \\ 2f(x) &= x^{2/3} \\ 2g(x) &= \pm \sqrt{x^{4/3} - 4(x^2{-}1)} \end{align}\]

ซึ่งพอเราพล็อตทั้งสองส่วนนี้แยกกันดู จะเห็นว่า $f$ นั้นมีหน้าตาคล้ายปีกนก ส่วน $g$ จะคล้ายวงรี

พล็อต $f$ (สีน้ำเงิน) และ $g$ (สีส้ม)

สังเกตว่า $g$ นั้นไม่ใช่ฟังก์ชัน เพราะยังแบ่งเป็นสองซีกบน-ล่างที่สะท้อนซึ่งกันและกัน แต่ตอนที่จะหา $f+g$ จะทำให้สองซีกนี้มีหน้าตาไม่สมมาตรกันแล้ว ซึ่งก็คือการบวกกันซีกบนจะทำให้ได้รูปทรงคล้ายภูเขายอดเรียบสองลูก ส่วนการบวกกันซีกล่างทำให้ได้หุบเหวแหลมลึกตรงกลางอันเดียว ซึ่งพอเราเอาผลลัพธ์สองซีกมาประกบกันก็จะได้รูปหัวใจที่เราคุ้นตานั่นเอง

พอมองเป็นผลบวกของสองซีกแบบนี้ก็ง่ายดี แล้วเราสามารถทำให้สมการนี้เรียบง่ายขึ้นได้อีกหรือเปล่า?

หัวใจ (no pun intended) สำคัญของสมการข้างต้น คือส่วน $f$ ต้องเป็นหุบเหวแหลมลึกตรงกลาง ส่วน $g$ นั้นอาจเป็นแค่วงกลมหรือวงรีง่ายๆ ก็เพียงพอ เพราะงั้นลองพิจารณา

\[\begin{align} 2f'(x) &= \abs{x} \\ 2g'(x) &= \pm \sqrt{4-3x^2} \\ y &= \frac{\abs{x} \pm \sqrt{4-3x^2}}2 \end{align}\]

คำนวณย้อนกลับโดยยกเลิกสูตรแก้สมการกำลังสองบนตัวแปร $y$ จะได้

\[y^2 -\abs{x}y + (x^2{-}1) = 0\]

พล็อตสมการ $y^2 - \abs{x}y + x^2 = 1$ (สีม่วง) เทียบกับสมการหัวใจก่อนหน้า (เส้นประสีแดง)

ซึ่งอาจจะเรียบง่ายกว่า(?) สวยงามกว่า(?) อย่างไรก็ตามสังเกตว่าสมการดังกล่าวติดค่าสัมบูรณ์ที่พจน์ตรงกลาง ซึ่งในแง่หนึ่งอาจจะถือว่ามันน่าเกลียดก็ได้ แต่ถ้าเราพยายามถอดค่าสัมบูรณ์นี้ทิ้งไป สิ่งที่จะได้กลับมาคือวงรีเฉียงๆ สองอันไขว้กันแทน

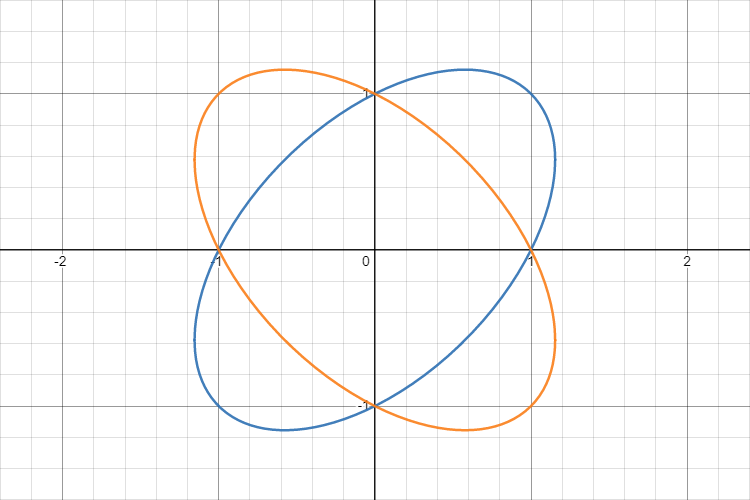
พล็อตสมการ $y^2 \pm xy + x^2 = 1$ เมื่อพจน์กลางเครื่องหมายเป็นบวก (สีน้ำเงิน) และลบ (สีส้ม)

แล้วถ้าเราอยากจะได้สมการเรียบง่ายสวยๆ แต่ยังคงไว้ซึ่งรูปทรงหัวใจเช่นเดิม เราจะทำอย่างไรได้บ้าง? ทางหนึ่งที่เป็นไปได้ก็คือเปลี่ยนไปพล็อตบนระบบพิกัดเชิงขั้วแทน ซึ่งมองค่าของฟังก์ชันเป็นระยะห่างจากจุดศูนย์กลางพิกัดออกไปในองศาที่แตกต่างกัน ดังนั้นเราอาจพิจารณารูปทรงอันแสนเรียบง่ายสองอันนี้

1. $u(\theta) = 1$ วงกลมที่มีระยะห่างจากจุดศูนย์กลางเท่ากับหนึ่งไม่ว่าจะพิจารณาในองศาไหน
2. $v(\theta)=\sin\theta$ วงกลมเส้นผ่านศูนย์กลางหนึ่งหน่วยที่สัมผัสตั้งฉากจุดศูนย์กลางพิกัดที่มุม $\pi/2$

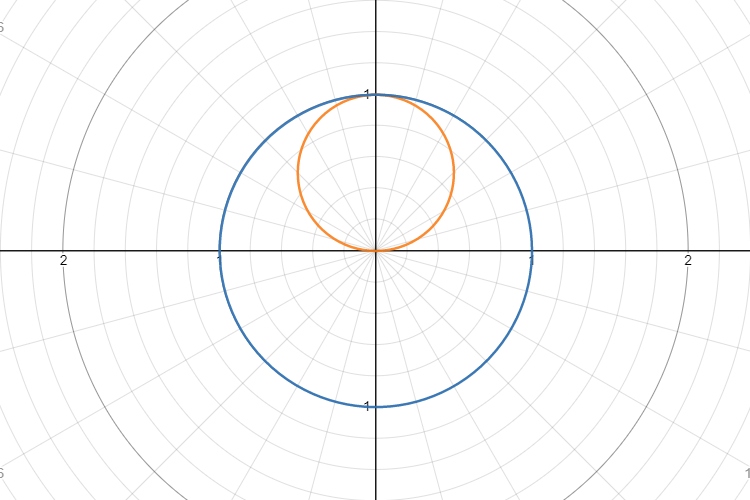
พล็อตฟังก์ชัน $u$ (สีส้ม) และ $v$ (สีน้ำเงิน) บนพิกัดเชิงขั้ว

สังเกตว่าเราจะเห็น $v$ แค่ครึ่งบนของพล็อต (ช่วง $0\le\theta<\pi$) นั่นก็เพราะว่าที่ครึ่งล่างนั้น (ช่วง $\pi\le\theta<2\pi$) ระยะห่างมีค่าติดลบ เส้นโค้งในครึ่งล่างจึงถูกวาดย้อนกลับไปอยู่ฝั่งครึ่งบนแทน และยังวาดทับกับเส้นข้างบนได้พอดิบพอดีอีกด้วย (สมบัติของฟังก์ชัน $\sin$)

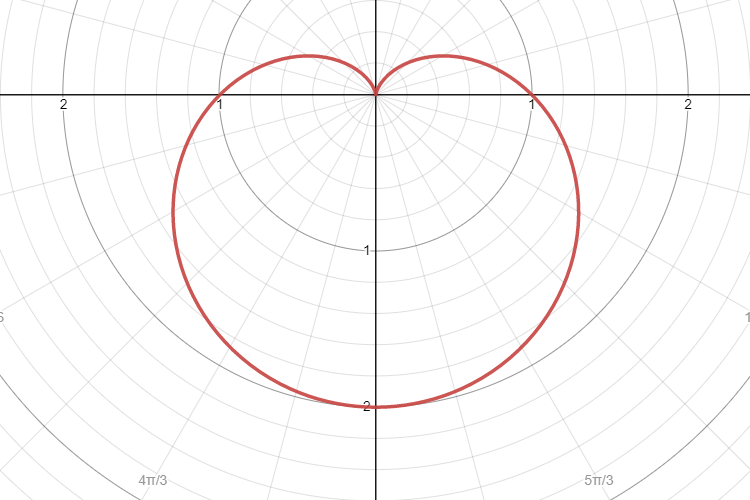
ดังนั้นเมื่อเราหา $u-v$ เราก็จะได้รูปหัวใจ (cardioid)แบบอ้วนป้อมหัวไม่แหลมกลับมานั่นเอง

พล็อต $r = 1 - \sin\theta$

ถึงแม้รูปทรงดังกล่าวอาจจะสวยสู้รูปทรงจากสมการแรกๆ ไม่ได้ แต่มันก็มีสมการที่เรียบง่ายกว่าอย่างเห็นได้ชัด และมันก็เป็นรูปทรงที่เกิดขึ้นอยู่บ่อยมากๆ รอบตัวเราอีกด้วย เช่น แสงเงาบนผิวน้ำในแก้วกาแฟที่โดนแดดยามเช้าส่องในมุมเฉียงๆ

สุดท้ายแล้วมันก็คงขึ้นกับว่าเราชอบแบบไหนมากกว่า? เพราะงั้นชอบแบบไหนก็บอกกันได้นะ 😉