ทวิภาวะ จุด-เส้นตรง
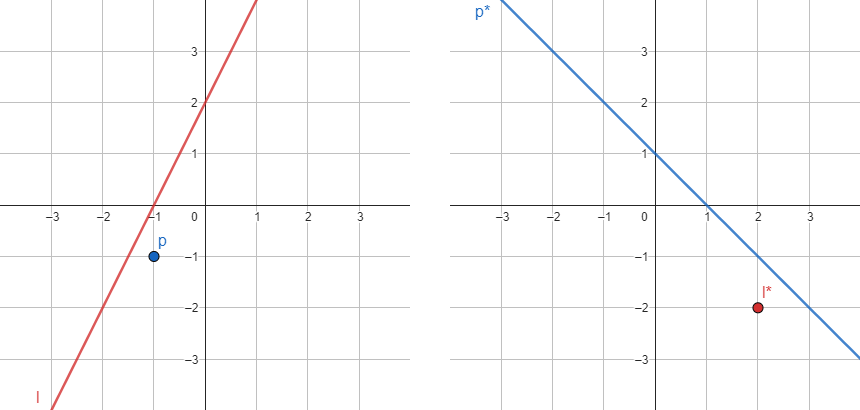
ความน่าตื่นตาตื่นใจของเรขาคณิตวิเคราะห์ที่ชาวกรีกโบราณน่าจะไม่มีวันคาดคิดถึง (เพราะสมัยนั้นยังไม่ได้ประดิษฐ์ระบบพิกัดคาร์ทีเซียนมาใช้งาน) คงหนีไม่พ้นแนวคิดทวิภาวะ (duality)1 ระหว่างจุดกับเส้นตรง ซึ่งก็คือ เริ่มจากเรามีจุด $p$ และเส้นตรง $\ell$ ที่นิยามผ่านสมการพิกัดว่า
\[\begin{align} p &= (a,b) \\ \ell &= mx - c \end{align}\]เราจะสร้าง “โลกคู่ขนาน” ที่แปลงวัตถุแต่ละชิ้นไปเป็นวัตถุคู่ส่วนกลับของมัน ในที่นี้คือ จุดจะถูกแปลงเป็นเส้น และเส้นจะถูกแปลงเป็นจุด ให้การเขียนสัญลักษณ์ดาวที่มุมขวาบนบ่งถึงการแปลงวัตถุให้เป็นคู่ส่วนกลับของมัน เรานิยามกฎการแปลงวัตถุไว้ว่า
\[\begin{align} p^\ast &= ax - b \\ \ell^\ast &= (m,c) \end{align}\]มองเผินๆ ก็ไม่รู้ว่าจะทำไปทำไม ยิ่งเมื่อคิดว่าเราสามารถเลื่อนจุดกำเนิดไปอยู่ตรงไหนก็ได้ ทวิภาวะของมันจึงไม่ได้มีเพียงแค่คำตอบเดียว เลยทำให้การแปลงดังกล่าวแอบดูยุ่งเหยิงไม่เป็นธรรมชาติ
(ซ้าย) โลกตั้งต้นของจุด $p$ และเส้น $\ell$ (ขวา) โลกคู่ขนานของเส้น $p^\ast$ และจุด $\ell^\ast$
แต่จริงๆ แล้วการแปลงเช่นนี้คงสมบัติอันน่าสนใจระหว่างจุดกับเส้นตรงไว้อย่างไม่น่าเชื่อ ซึ่งก็คือ หากในโลกตั้งต้นนั้นเส้นตรง $\ell$ อยู่เหนือจุด $p$ แล้วในโลกคู่ขนานเราจะได้ว่าเส้นตรง $p^\ast$ นั้นก็จะอยู่เหนือจุด $\ell^\ast$ ด้วย
การจะเห็นเรื่องนี้ได้อาจต้องเริ่มจากการโยนเรขาคณิตทิ้งไปก่อน แล้วหันไปพิจารณากับตัวสมการตรงๆ โดยเราจะมองว่าเส้นตรงคือฟังก์ชัน $\ell(x) = mx-c$ ดังนั้น เมื่อเราคำนวณค่า $\ell(a)$ แล้วเอาไปเทียบกับ $b$ เราจะตีความย้อนกลับมาเป็นเรขาคณิตได้ว่า
- เมื่อ $\ell(a) < b$ นั่นคือเส้น $\ell$ จะอยู่ใต้จุด $p$
- เมื่อ $\ell(a) > b$ นั่นคือเส้น $\ell$ จะอยู่เหนือจุด $p$
- เมื่อ $\ell(a) = b$ นั่นคือเส้น $\ell$ จะทับจุด $p$ พอดี
เพื่อความสะดวก ต่อไปนี้จะขอใช้สัญลักณ์ $\lessgtr$ เพื่อแสดงการเปรียบเทียบระหว่างสองข้างอสมการ โดยมองว่ามันคือการเขียนรวบย่อของสามกรณีที่มีโครงสร้างเดียวกัน อันได้แก่ น้อยกว่า/เท่ากับ/มากกว่า มารวมไว้ในที่เดียว2 นอกจากนี้ในบริบทเรขาคณิต สัญลักษณ์ดังกล่าวจะแสดงว่าเส้นที่สนใจนั้นอยู่ ใต้/ทับ/เหนือ จุดที่สนใจอีกด้วย ดังนั้น
\[\ell \lessgtr p \iff ma - c \lessgtr b \iff am-b \lessgtr c \iff p^\ast \lessgtr \ell^\ast \tag*{$\blacksquare$}\]ความเป็นทวิภาวะเช่นนี้ก็เจ๋งดี แต่ว่าแล้วมันมีประโยชน์ตรงไหน? แน่นอนว่าถ้าเรามีวัตถุแค่สองชิ้น (หนึ่งเส้นกับหนึ่งจุด) ก็อาจไม่มีประโยชน์อะไรจริงๆ นอกจากความเจ๋ง แต่ถ้าเราลองเพิ่มวัตถุเข้าไปดู จะเห็นได้ว่า
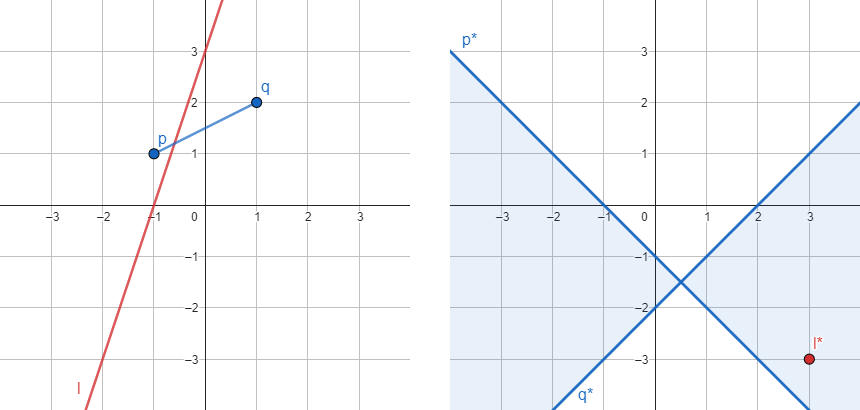
- ในโลกตั้งต้นที่มีจุดสองจุด $p,q$ พร้อมเส้นตรง $\ell$ ที่ลากผ่านสองจุดนั้น จะได้ว่าในโลกคู่ขนานก็จะมีเส้นตรงสองเส้น $p^\ast,q^\ast$ ที่ทั้งคู่ตัดกันที่จุด $\ell^\ast$ ด้วย
- ในโลกตั้งต้นที่มีส่วนของเส้นตรง $\overline{pq}$ และเส้นตรง $\ell$ ที่ลากไปตัดส่วนของเส้นตรง จะได้ว่าในโลกคู่ขนานจะมีบริเวณที่กวาดเชิงมุมจากเส้นตรง $p^\ast$ ไปยังเส้นตรง $q^\ast$ ซึ่งมีจุด $\ell^\ast$ ปรากฏอยู่ภายในบริเวณนี้
(ซ้าย) ส่วนของเส้นตรง $\overline{pq}$ ในโลกตั้งต้น (ขวา) บริเวณที่ $\overline{pq}$ แปลงร่างมากวาดได้ในโลกคู่ขนาน
ดูท่าว่าในโลกคู่ขนานแห่งนี้ ข้าพเจ้าจะใช้แค่สัญชาตญาณทางเรขาคณิตไม่ได้แล้วหล่ะสิ 😭 (และขอขอบคุณโลกนี้ที่มีคนทำเว็บแอพไว้ให้ลองเล่น!)

author