หนึ่งในคำถามสุดคลาสสิกในเรขาคณิตเชิงคำนวณ เริ่มจากให้ข้อมูลตั้งต้นที่ประกอบด้วยจุด $n$ จุดบนระนาบ เราจะถามว่า ภายในพิสัย (range) ที่เราสนใจนั้นมีจุดใดปรากฏตัวขึ้นมาบ้าง?

ตัวอย่างง่ายๆ ตรงไปตรงมา ก็เช่น สนใจแผนที่จังหวัดแห่งหนึ่ง โดยให้แต่ละจุดนั้นแทนตำแหน่งบ้านเรือน และให้พิสัยเป็นวงกลมรัศมีสี่กิโลเมตรโดยเลือกจุดศูนย์กลางเป็นตำแหน่งใดก็ได้บนแผนที่ เช่นนี้แล้วผลลัพธ์การค้นหาบนพิสัยก็จะตอบเราได้ว่า หากเราสร้างร้านอาหารตรงจุดศูนย์กลางที่เลือกนั้นแล้ว เราสามารถคาดหวังลูกค้าในอนาคตว่าอาจจะเป็นใครได้บ้าง (หรือเราไม่จำเป็นต้องรู้ว่าเป็นใครบ้างก็ได้ แค่นับจำนวนรวมเพื่อประมาณการว่ามีลูกค้าเท่าไหร่ก็พอ)

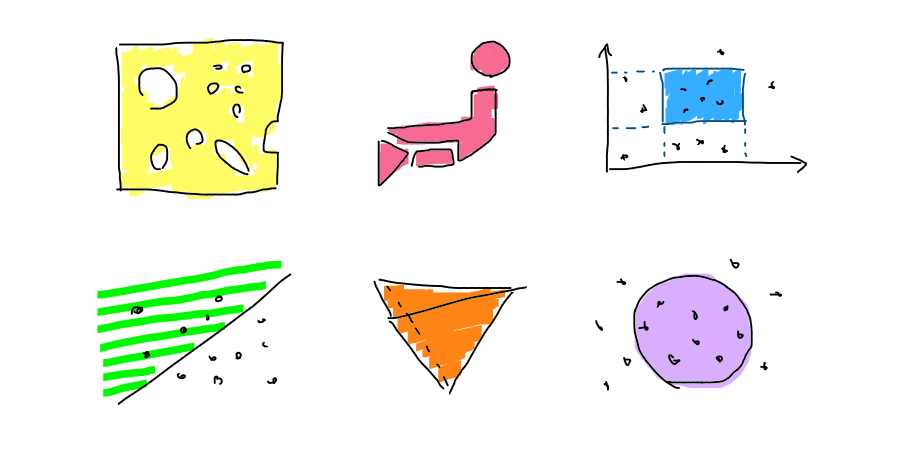
รูปร่างหน้าตาของพิสัยที่เราสนใจนั้นอาจมีความสลับซับซ้อนเป็นรูปทรงใดก็ได้ เช่น สวิสชีสที่มีรูพรุนอยู่อย่างกระจัดกระจาย (ซึ่งก็น่าจะไม่มีประโยชน์เท่าไหร่) หรือรูปทรงแบ่งเขตแดนการปกครอง แต่โดยพื้นฐานแล้ว เราจะสนใจรูปทรงง่ายๆ ดังนี้

1. สี่เหลี่ยมขนานแกน (orthogonal rectangle) ซึ่งดูเผินๆ อาจรู้สึกไม่เป็นธรรมชาติเท่าไหร่ แต่มันมีจุดที่ได้ใช้บ่อยในงานเชิงฐานข้อมูล เช่น ค้นหาพนักงานที่มีเงินเดือนในช่วง 100k-200k และมีอายุระหว่าง 18-25 ปี … ก็อาจนับได้ว่าเป็นเรขาคณิตอีกแบบนึงหละมั้ง?
2. ครึ่งระนาบ (half plane) อาจฟังดูคล้ายกับสี่เหลี่ยมขนานแกนข้างต้น แต่คราวนี้เราไม่ได้มีข้อจำกัดของการขนานแกนแล้ว นั่นก็คือมันจะเป็นธรรมชาติมากขึ้นสำหรับปัญหาเชิงเรขาคณิต
3. สามเหลี่ยม (หรือก็คือ simplex) รูปทรงที่เล็กและง่ายที่สุดใน $n$ มิติ ที่มีจำนวนจุดยอด $n{+}1$ จุด ซึ่งจริงๆ เราอาจมองมันเป็นอินเตอร์เซกชันของครึ่งระนาบจำนวน $\binom{n+1}{n}$ แผ่นก็ได้
4. วงกลม (ไปจนถึง hypersphere) อันนี้ก็เป็นรูปทรงที่เข้าใจได้ง่ายอีกอันนึง แต่ในเชิงการคำนวณอาจยุ่งยากซับซ้อนกว่าแค่ครึ่งระนาบ/สามเหลี่ยมได้มากๆ

ส่วนรูปทรงที่ซับซ้อนกว่านี้ก็สามารถสร้างได้จากการหายูเนียน/อินเตอร์เซกชันของรูปทรงพื้นฐานนั่นเอง

ตัวอย่างพิสัยแบบต่างๆ (1) แผ่นชีส (2) รูปหลายเหลี่ยม (3) สี่เหลี่ยมขนานแกน (4) ครึ่งระนาบ (5) ซิมเพล็กซ์ (6) ทรงกลม

ทีนี้ กลับมาที่โจทย์หลักของเรา ถ้าเราต้องการทราบว่ามีจุดใดบ้างอยู่ในพิสัยนั้นเพียงแค่ครั้งเดียว เราต้องใช้เวลาอย่างน้อยเป็น $O(n)$ แน่ๆ ซึ่งก็คือเราจะวิ่งไล่เช็คทีละจุดเลยว่ามันอยู่ในพิสัยหรือไม่ (และเราอาจใช้เวลามากกว่านี้ได้อีกเมื่อรูปทรงของพิสัยมันมีความซับซ้อนกว่ารูปทรงพื้นฐาน)

แต่ธรรมชาติของโจทย์ปัญหานี้ในโลกจริง เรามักจะถามคำถามใหม่ซ้ำๆ บนเซตของจุดอันเดิมเรื่อยๆ (เช่น จากข้อมูลแผนที่บ้าน เราอาจทดลองเปลี่ยนจุดตั้งร้านอาหารเป็นจำนวนหลายครั้งจนกว่าจะพอใจ) ดังนั้นมันจะดีกว่าถ้าเราเสียเวลาคำนวณโครงสร้างข้อมูลบนจุดเหล่านั้นทิ้งไว้ก่อนเลย เพื่อให้การถามคำถามแต่ละครั้งภายหลังนั้นถูกตอบได้อย่างรวดเร็ว

เราเรียกแนวคิดการออกแบบอัลกอริทึมเพื่อแก้โจทย์ปัญหาเช่นนี้ว่า การประมวลผลล่วงหน้า-สืบค้น (preprocess-query) ซึ่งก็คือ โครงสร้างการทำงานของอัลกอริทึมจะถูกแบ่งเป็น 2 ห้วงขณะที่แยกออกจากกัน ได้แก่

1. ห้วงแห่งการประมวลผลทิ้งไว้ล่วงหน้า เราจะรับข้อมูลจุด $n$ จุดเข้ามาคำนวณเป็นโครงสร้างข้อมูลทิ้งไว้ (ทำแค่ครั้งเดียว) โดยทั่วไปเราจะไม่กังวลเรื่องความเร็วเท่าไหร่ (ขอแค่ไม่ให้ช้าจนเกินไป) แต่จะสนใจขนาดพื้นที่สำหรับจัดเก็บโครงสร้างข้อมูลเป็นหลัก
2. ห้วงแห่งการสืบค้นคำตอบ เราจะรับพิสัยที่ต้องการถามว่ามีจุดใดอยู่ในนั้นบ้าง ซึ่งก็คือเราจะเอาพิสัยไปค้นหาบนโครงสร้างข้อมูลที่คำนวณทิ้งไว้นั่นเอง แน่นอนว่าเราจะสนใจความเร็วในการตอบคำถามเป็นหลัก นอกจากนี้เราจะทำงานในห้วงนี้ซ้ำๆ บนคำถามใหม่ๆ ที่ไม่เหมือนเดิมอีกด้วย

ลองดูตัวอย่างใน 1 มิติกันดีกว่า สมมติให้ข้อมูล $S=\lbrace s_1,s_2,\dots,s_n \rbrace$ แทนตำแหน่งกระถางแคคตัสที่อยู่ติดริมรั้ว (ในหน่วยเซนติเมตรนับจากมุมรั้ว) อยากจะทราบว่า ถ้าเราต้องการทุปรั้วไปสร้างประตูในช่วงปิด $[\ell,r]$ เราจะต้องย้ายกระถางแคคตัสทั้งหมดกี่กระถาง

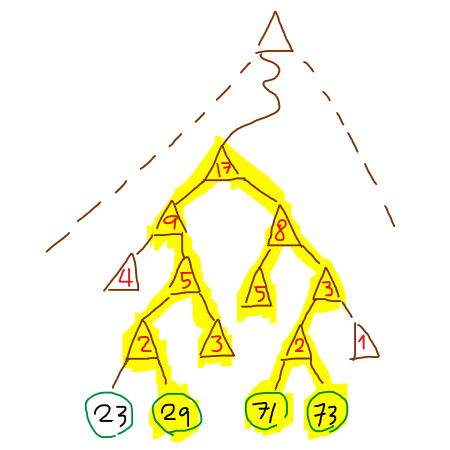
เทคนิคหนึ่งที่ใช้ได้เสมอๆ ในโลกของปัญหาเชิงการคำนวณในคอมพิวเตอร์ ก็คือการค้นหาแบบทวิภาค (binary search) ดังนั้นเราจะใช้โครงสร้างข้อมูลแบบต้นไม้มีราก (rooted tree) เพื่อเก็บข้อมูลว่า ในช่วง $[a,b)$ ที่สนใจนั้น เรานับกระถางแคคตัสได้กี่กระถาง (เก็บค่าเป็นน้ำหนักประจำโหนด) แล้วก็เรียกตัวเองบนช่วง $[a,c)$ กับ $[c,b)$ ซ้อนลงไปเรื่อยๆ

หลังจากที่เราประมวลผลข้อมูลทิ้งไว้เสร็จแล้ว เมื่อเราต้องการสืบค้นพิสัย $[\ell,r]$ ว่ามีกระถางแคคตัสเป็นจำนวนเท่าใด เราก็แค่ท่องลงไปในต้นไม้ตามขอบของพิสัยทั้งสองฝั่ง แล้วก็คำนวณผลรวมทั้งหมดของน้ำหนักโหนดที่อยู่ภายในพิสัยนั่นเอง

ตัวอย่างโครงสร้างข้อมูลและการสืบค้น เมื่อพิจารณาพิสัย $[28,73]$ ซึ่งให้คำตอบว่าต้องย้าย 11 กระถาง

จะเห็นว่าการสร้างต้นไม้ใช้เวลา $O(n\log n)$ และกินพื้นที่เก็บข้อมูล $O(n)$ ส่วนการสืบค้นก็กินเวลาอีกครั้งละ $O(\log n)$ เท่านั้น ซึ่งในโลกของอัลกอริทึมแล้ว นี่คือความเร็วและขนาดพื้นที่จัดเก็บที่แทบจะดีที่สุดในอุดมคติเลยทีเดียว

อย่างไรก็ตาม สำหรับปัญหาในมิติที่สูงขึ้นไป (แอบเฉลยตรงนี้เลยแล้วกันว่า) เราไม่มีอัลกอริทึมที่ทำงานได้ดีตามอุดมคติของเราอีกต่อไป ถึงตรงนี้แนวทางการพัฒนาอัลกอริทึมจะแยกออกเป็นสองสาย โดยสายแรกจะให้ความสำคัญกับการบีบขนาดพื้นที่เก็บข้อมูลให้เล็ก (แต่ยอมให้เวลาสืบค้นคำตอบนานหน่อย) แน่นอนว่าสายที่สองก็จะให้ความสำคัญกับการค้นคำตอบได้เร็ว (แต่ใช้พื้นที่จัดเก็บบวม)

แล้วเราจะกลับมาดูรายละเอียดของอัลกอริทึมสำหรับมิติอื่นๆ ในตอนถัดไป

neizod

author