ในตอนที่ผ่านมาเราได้เห็นอัลกอริทึมสำหรับการค้นหาบนพิสัยแบบ 1 มิติไปแล้ว คราวนี้เราจะมาพิจารณาปัญหาในมิติที่สูงขึ้นไป โดยเราจะมองผ่านกรณี 2 มิติเป็นตัวอย่างประกอบ อย่างไรก็ตาม ในภาพรวมแล้วเทคนิคอัลกอริทึมที่กำลังนำเสนอนี้สามารถถูกนำไปประยุกต์ใช้กับมิติใดๆ ก็ได้ (เพียงแค่ว่าในรายละเอียดแล้วเราจะได้ค่าความซับซ้อนแย่ลง)

มาทบทวนปัญหาที่เราต้องการแก้อีกรอบ พิจารณาเซต $S=\lbrace s_1,s_2,\dots,s_n\rbrace$ ซึ่งเก็บจุดใน 2 มิติ เราต้องการนำ $h$ ซึ่งเป็นพิสัยแบบครึ่งระนาบไปสืบค้นว่ามีจุดเป็นจำนวนเท่าไหร่ที่ปรากฏอยู่บน $h$ เราจะแก้ปัญหานี้ได้อย่างไร? อะไรคือโครงสร้างข้อมูลที่เราต้องการใช้?

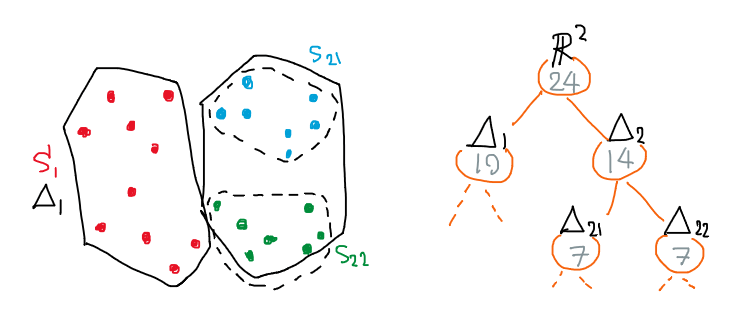
เราจะทดลองคิดวิธีแก้ปัญหานี้แบบง่ายๆ กันก่อน โดยท่าที่ง่ายที่สุดก็คือการพยายามมองปัญหาด้วยกรอบของอัลกอริทึม-โครงสร้างข้อมูลที่อิงบนต้นไม้ทวิภาค (binary tree) ที่เราจะแบ่งเซต $S$ ออกเป็นสองฝาก ฝากละเท่าเท่ากัน นั่นคือ $S = S_1 \cup S_2$ โดยสำหรับแต่ละซับเซต $S_i$ เราจะเก็บข้อมูลสองอย่าง คือ ขนาด $n_i=\abs{S_i}$ และรูปทรง $\Delta_i$ ที่คลุมซับเซตนั้นๆ ในขั้นต้นนี้เราจะใช้รูปทรงคอนเวกซ์ฮัลล์ (convex hull) มาครอบ แล้วหลังจากนั้นก็เวียนเกิดลงไปเรื่อยๆ จนถึงใบของต้นไม้ที่เก็บข้อมูลเพียงแค่จุดเดียว ดังตัวอย่างตามภาพต่อไปนี้

การแบ่งซับเซตของจุดที่สนใจ และโครงสร้างข้อมูลแบบต้นไม้ที่เก็บข้อมูลของการแบ่งนั้น

เนื่องจากต้นไม้ทวิภาคข้างต้นนี้เป็นโครงสร้างข้อมูลที่เรารู้จักกันดี ดังนั้นมันจึงกินพื้นที่จัดเก็บแค่ $O(n)$ ไม่ได้มีอะไรแปลกประหลาดพิสดารให้เราต้องกังวลแต่อย่างใด

และด้วยโครงสร้างข้อมูลเช่นนี้ ก็ทำให้เราได้อัลกอริทึมที่ทำงานอย่างตรงไปตรงมา นั่นคือ รับข้อมูลนำเข้าพิสัยครึ่งระนาบ $h$ ที่เราต้องการสืบค้น หลังจากนั้นก็วนเข้าไปดูลูกๆ ของโหนดรากในต้นไม้ว่า $\Delta_i$ นั้นทับซ้อนกับ $h$ อย่างไร

• ถ้า $\Delta_i$ อยู่ข้างใน $h$ ทั้งหมด แปลว่าทุกจุดใน $S_i$ ต้องปรากฏตัวในพิสัยแน่นอน นั่นคือเรานำค่า $n_i$ ไปบวกเพิ่มในคำตอบได้เลย
• ถ้า $\Delta_i$ อยู่ข้างนอก $h$ ทั้งหมด แปลว่าไม่มีจุดใดเลยใน $S_i$ ที่อยู่ในพิสัยเลย เราก็ไม่ต้องสนใจค่า $n_i$ ไม่ต้องสนใจโหนดนี้
• ถ้า $\Delta_i$ อยู่ทั้งข้างในและข้างนอก $h$ หรือก็คือ เส้นตรง $\ell(h)$ ที่อยู่บนขอบของครึ่งระนาบนั้นตัดผ่าน $\Delta_i$ สำหรับกรณีนี้เราก็จะเรียกตัวเองวนลงไปยังลูกๆ ของโหนดนั้น

อัลกอริทึมนี้ก็ดูปรกติมาตรฐานดีไม่ควรมีอะไรทำงานพลาด แต่ด้วยการใช้งานร่วมกับโครงสร้างข้อมูลข้างต้น มันกลับไม่ได้ช่วยให้การสืบค้นเป็นไปได้รวดเร็วเท่าใดนัก ซึ่งเกิดจากหลายประเด็น เช่น

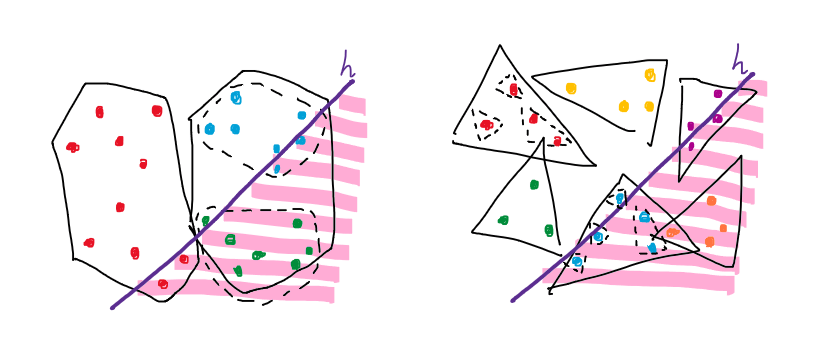
1. แม้ว่าแต่ละ $\Delta_i$ จะเป็นคอนเวกซ์ฮัลล์ (เข้าใจและเห็นภาพในระดับคอนเซปต์ได้ง่าย) แต่ในการทำงานจริงเราจะต้องเสียเวลานานในการเช็คว่า $\Delta_i$ นั้นซ้อนทับกับ $h$ แบบไหน เพราะว่าเรามีขอบของฮัลล์ที่มากได้ถึง $O(n)$ ขอบ
2. สำหรับข้อมูลนำเข้า $h$ บางอัน อัลกอริทึมดังกล่าวอาจทำงานได้ช้าอยู่ดี เพราะว่า $\ell(h)$ ดันตัดผ่า $\Delta_i$ เป็นจำนวนมาก ทำให้เราต้องเรียกตัวเองซ้อนลงไปในโหนดลูกหลายโหนด ซึ่งผิดไปจากความตั้งใจเดิมของการใช้ต้นไม้ทวิภาคที่เราจะเวียนเกิดแค่ชั้นละโหนดเดียว

(ซ้าย) ตัวอย่างคอนเวกซ์ฮัลล์ที่โดนตัดหลายชิ้นมากเกินไป (ขวา) วิธีแก้ปัญหาโดยการเปลี่ยนไปคลุมซับเซตด้วยสามเหลี่ยม

แล้วเราจะทำอย่างไรเพื่อแก้ปัญหานี้? สำหรับประเด็นแรกนั้นเราก็แค่ไม่ต้องใช้คอนเวกซ์ฮัลล์ แต่เปลี่ยนไปใช้สามเหลี่ยมแทนเพราะมันมีจำนวนด้านเป็นค่าคงที่ (อันที่จริง ไม่ต้องใช้สามเหลี่ยมก็ได้ อาจใช้สี่เหลี่ยมหรือวงกลมก็ไม่ต่างกันมาก ประเด็นสำคัญคือต้องทำให้เช็คได้ง่ายและเร็วว่า $\ell(h)$ ตัดผ่านรูปทรงเหล่านั้น) การเปลี่ยนแปลงเช่นนี้ไม่ได้มีผลอะไรกับความถูกต้องของอัลกอริทึม เพียงแค่อาจทำให้วาดภาพออกมาดูยากขึ้นแค่นั้นเอง อนึ่ง เรายินยอมให้สามเหลี่ยมแต่ละชิ้นซ้อนทับกันได้ เพียงแต่ว่าจุดที่สนใจจะต้องเลือกว่าจะอยู่ในสามเหลี่ยมใดสามเหลี่ยมหนึ่งเท่านั้น

ส่วนในประเด็นที่สอง เอาจริงหากเราตั้งใจสังเกต แม้ว่าในการเวียนเกิดบางชั้น รูปทรง $\Delta$ จากโหนดลูกทั้งคู่จะโดนตัดพร้อมกัน แต่ถ้าเราแบ่งซับเซตได้ดี ก็ยังมีอีกหลายชั้นที่ $\Delta$ ในโหนดลูกไม่โดนตัดทั้งคู่เช่นกัน อย่างไรก็ตามการวิเคราะห์ว่าชั้นไหนโดนตัดไม่โดนตัดบ้างนั้นทำได้ยาก วิธีที่ง่ายกว่าก็คือไม่ต้องจำกัดตนเองว่าต้องใช้ต้นไม้ทวิภาค แต่ไปใช้ต้นไม้ที่มีโหนดลูกๆ จำนวนมากกว่าแค่สองโหนดแทน ซึ่งก็คือ เราจะแบ่ง $S$ ออกเป็น $r$ ซับเซตแทน (ค่า $r$ เป็นพารามิเตอร์ที่เราเลือกปรับค่าได้) โดยให้แต่ละซับเซตมีขนาดใกล้เคียงกัน (พูดอย่างรัดกุมคือ $\abs{S_i} \le 2n/r$) ข้อดีของการทำเช่นนี้ก็คือ จากงานของ Matoušek ในปี 1991 ได้พิสูจน์ไว้ว่าจะมีการแบ่งซับเซตบางแบบที่ทำให้รูปทรง $\Delta$ โดนตัดเพียงแค่ $O(\sqrt{r})$ ชิ้นเท่านั้น ซึ่งก็คือจะช่วยลดความกังวลเรื่องจำนวนครั้งที่เราต้องเวียนเกิดลงไปได้

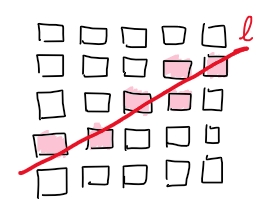
การพิสูจน์เรื่อง $O(\sqrt{r})$ นั้นมีรายละเอียดเยอะเกินกว่าขอบเขตของเนื้อหาในตอนนี้ แต่การพิสูจน์อย่างคร่าวๆ เพื่อให้คุ้นชินกับสหัชญาณของทฤษฎีดังกล่าว ก็อาจทำได้ผ่านภาพตัวอย่างง่ายๆ เช่นนี้

พูดอีกครั้งอย่างรัดกุมก็คือ จากเซต $S$ เราสามารถสร้างพาร์ทิชัน $\Psi(S) = \lbrace (S_1,\Delta_1), \dots, (S_r,\Delta_r) \rbrace$ ที่ไม่ว่าเราจะพิจารณาเส้นตรง $\ell$ ใดๆ จะมี $\Delta$ เพียงแค่ $O(\sqrt{r})$ ชิ้นเท่านั้นที่โดนตัด เราเรียก $\Psi(S)$ เช่นนี้ว่าการแบ่งพาร์ทิชันด้วยซิมเพล็กซ์ (simplicial partition – คำว่า simplicial นั้นมาจาก simplex ซึ่งก็คือรูปทรงหลายเหลี่ยมที่เรียบง่ายที่สุดประจำมิตินั้นๆ)

---

แล้วความซับซ้อนของเวลาการสืบค้นข้อมูลบนโครงสร้างข้อมูลแบบใหม่นี้ (ใช้สามเหลี่ยม + แบ่งชั้นละ $r$ ชิ้น) มันเป็นเท่าไหร่กันหละ? เอาจริงๆ คำถามนี้มันมีรายละเอียดที่วิเคราะห์ได้ยุ่งยากพอสมควร ดังนั้นแทนที่จะอธิบายรวดเดียวจบ จะขอแบ่งอธิบายสองครั้งแทน โดยครั้งแรกจะลดรูปปัญหาให้ง่ายลงเพื่อให้เห็นคำตอบคร่าวๆ ในเชิงสหัชญาณก่อน แล้วจึงค่อยอธิบายซ้ำอีกครั้งแบบลงรายละเอียดให้แม่นยำมากขึ้น

โดยความสัมพันธ์เวียนเกิดตั้งต้นที่บ่งถึงความเร็วของการสืบค้นข้อมูล ซึ่งถอดออกมาตรงๆ ได้จากอัลกอริทึมข้างต้นก็คือ

\[Q(n) = r + \sum_{\substack{1 \le i \le n \\ \Delta_i \cap \ell(h)}} Q(n_i) \tag{1} \label{eq:recurrent}\]

พจน์ $r$ นั้นบอกว่ายังไงเราก็ต้องไล่พิจารณาแต่ละ $\Delta_i$ ว่ามันทับซ้อนอย่างไรกับ $h$ ส่วนพจน์ผลรวมของ $Q(n_i)$ นั้นคือการเวียนเกิดลงไปเมื่อ $\Delta_i$ ตัดกับ $\ell(h)$

ถึงตรงนี้เราจะลองวิเคราะห์แบบง่ายก่อน นั่นคือ เนื่องจากมี $O(\sqrt{r})$ ที่ต้องเวียนเกิด และเมื่อเวียนเกิดแต่ละครั้งเราจะเหลือจุดที่สนใจในชั้นถัดไปเพียง $n/r$ ดังนั้น $\eqref{eq:recurrent}$ จะกลายเป็น

\[Q(n) = r + \sqrt{r} \cdot Q(n/r) \tag{2} \label{eq:recurrent-simple}\]

ความแปลกของ $\eqref{eq:recurrent-simple}$ ก็คือ นอกจาก $Q(n/r)$ ที่เวียนเกิดลงไปแล้ว พจน์อื่นนั้นไม่อิงกับค่า $n$ ซึ่งเป็นขนาดข้อมูลตั้งต้นเลย แต่ไปอิงกับค่าคงที่ $r$ แทน เพราะงั้นการแก้ความสัมพันธ์เวียนเกิดนี้ก็ง่ายๆ แค่ถามว่าต้องเวียนเกิดลงไปลึกกี่ชั้นถึงจะจบ ซึ่งก็คือ

\[k = \left\lceil \log_r n \right\rceil \tag{3} \label{eq:depth-simple}\]

ดังนั้น กลับไปทำ $\eqref{eq:recurrent-simple}$ ก็จะได้

\[\begin{align} Q(n) &= r + \sqrt{r} \cdot Q(n/r) \\ &= r + r\sqrt{r} + \sqrt{r}^2\cdot Q(n/r^2) \\ &\;\;\vdots \\ &= r + r\sqrt{r} + r\sqrt{r}^2\cdot + \dots + r\sqrt{r}^{k-1} + \sqrt{r}^k \end{align}\]

สังเกตว่าทุกพจน์ยกเว้นพจน์สุดท้ายนั้นมี $r$ คูณติดอยู่ทั้งหมด ดังนั้นพจน์ที่เติบใหญ่จนครอบงำทั้งหมดก็คือพจน์รองสุดท้ายซึ่งมีค่าเป็น $r\sqrt{r}^{k-1}=\sqrt{r}^{k+1}$ นั่นเอง อย่างไรก็ตาม เนื่องจาก $r$ เป็นค่าคงตัว ดังนั้นเพื่อความง่ายเราอาจมองเลขยกกำลังเหลือแค่ $k$ ก็ได้โดยไม่ต้องบวกหนึ่งเพิ่ม (หรือพูดอีกนัยหนึ่งก็คือ ไม่ว่าเราจะหยิบพจน์รองสุดท้ายหรือพจน์สุดท้ายมาใช้วิเคราะห์ก็ไม่ต่างกัน) เพราะฉะนั้น

\[Q(n) = O(\sqrt{r}^k)\]

ถึงตรงนี้ขอให้ระลึกถึงเอกลักษณ์ลอการิทึมพื้นฐาน ที่ทำให้เราสามารถแปลงค่าของการติดลอการิทึม/เลขยกกำลังกลับไปกลับมาได้ว่า

\[r = n^{\log_n r} = n^{\log r / \log n} = n^{1/\log_r n} = n^{1/k}\]

จึงทำให้ได้

\[Q(n) = O(\sqrt{n}) \tag{4} \label{eq:time-simple}\]

หรือก็คือเวลาที่ใช้ในการสืบค้นพิสัย ควรมีความเร็วประมาณรากที่สองของขนาดข้อมูลตั้งต้นนั่นเอง

ย้ำอีกครั้งว่าการวิเคราะห์ข้างตั้น (ตั้งแต่ $\eqref{eq:recurrent-simple}$ จนถึง $\eqref{eq:time-simple}$) นี้ไม่แม่นยำซะทีเดียว โดยจุดที่เราพลาดไปก็คือ

1. จำนวน $\Delta$ ที่โดน $\ell(h)$ ตัดผ่านคือ $O(\sqrt{r})$ ซึ่งเราไม่สามารถแทนด้วยแค่ $\sqrt{r}$ แต่ต้องแทนด้วย $c\sqrt{r}$ เมื่อ $c$ เป็นค่าคงที่
2. ในแต่ละชั้นที่เราเวียนเกิดลงไป เราสามารถลดขนาดปัญหาลงได้เหลือแค่ $2n/r$ ไม่ใช่ว่าลดเป็นค่าเฉลี่ยที่ $n/r$

ดังนั้น ความสัมพันธ์เวียนเกิด $\eqref{eq:recurrent-simple}$ จึงควรกลายเป็น

\[Q(n) = r + c\sqrt{r} \cdot Q(2n/r) \tag{5} \label{eq:recurrent-precise}\]

นอกจากนี้ ความลึกของการเวียนเกิด $\eqref{eq:depth-simple}$ ก็ต้องกลายเป็น

\[k = \left\lceil \log_{r/2} n \right\rceil \tag{6} \label{eq:depth-precise}\]

โชคดีที่อย่างน้อยเราก็ยังวิเคราะห์ส่วนที่เหลือในทำนองเดิมได้ นั่นก็คือกระจายการเวียนเกิด $\eqref{eq:recurrent-precise}$ ด้วยความลึก $\eqref{eq:depth-precise}$ แล้วจับเอาพจน์สุดท้าย (หรือพจน์รองสุดท้าย) ที่ชนะครอบงำพจน์อื่นๆ ทั้งหมดมาวิเคราะห์ต่อก็เพียงพอ ซึ่งก็คือ

\[\begin{align} Q(n) &= O\left( (c\sqrt{r})^k \right) \\ &= O\left( c^k \cdot \frac{\sqrt{2}^k}{\sqrt{2}^k} \cdot \sqrt{r}^k \right) \\ &= O\left( c^k \cdot \sqrt{2}^k \cdot \sqrt{\frac{r}2}^k \right) \\ &= O\left( (c\sqrt2)^k \cdot \sqrt{n} \right) \end{align}\]

ถึงตรงนี้ เราจะพยายามจัดรูป $(c\sqrt2)^k$ ให้อยู่ในรูปของ $n$ โดยอาศัยข้อสังเกตที่ว่า

\[k = \log_{r/2} n = \log_{r/2} n \cdot \log_{c\sqrt2} c\sqrt2 = \log_{c\sqrt2} n \cdot \log_{r/2} c\sqrt2\]

ดังนั้น

\[(c\sqrt2)^k = n^{\log_{r/2}c\sqrt2}\]

จึงทำให้เราได้

\[Q(n) = O(n^{\log_{r/2}c\sqrt2} \cdot \sqrt{n})\]

เอาจริงๆ ส่วนเลขชี้กำลังนี้ก็แอบดูยาวไปนิดนึง แต่จากการวิเคราะห์คร่าวๆ ที่ผ่านมาใน $\eqref{eq:time-simple}$ มันช่วยให้เราเดาได้ว่าเลขชี้กำลังนี้ควรมีค่าเล็กๆ เพราะว่าเราสามารถเลือกค่า $r$ เป็นเท่าไหร่ก็ได้ (ยิ่ง $r$ ใหญ่ก็ยิ่งบีบให้เลขชี้กำลังเข้าใกล้ศูนย์ได้) ดังนั้นเราจะกำหนดตัวแปร

\[\varepsilon = \log_{r/2}c\sqrt2 \tag{7} \label{eq:epsilon}\]

ซึ่งก็คือเราจะได้ข้อสรุปว่า

\[Q(n) = O(n^\varepsilon \cdot \sqrt{n}) = O(n^{1/2+\varepsilon}) \tag{8} \label{eq:time-precise}\]

แล้วพารามิเตอร์ $r$ ควรมีค่าเป็นเท่าไหร่? นั่นก็ขึ้นอยู่กับว่าเราต้องการบีบค่า $\varepsilon$ ให้เล็กเป็นเท่าไหร่นั่นเอง โดยเราสามารถคำนวณย้อนได้ผ่านการย้ายข้างสมการ $\eqref{eq:epsilon}$ นั่นเอง

\[r = \left\lceil 2(c\sqrt2)^{1/\varepsilon} \right\rceil \tag{9} \label{eq:param-epsilon}\]

---

แล้วถ้าเราต้องการสืบค้นด้วยพิสัยแบบอื่นนอกเหนือจากแค่ครึ่งระนาบหล่ะ? ใจความสำคัญของอัลกอริทึมนี้คือการเช็คให้ได้เร็วว่าพิสัยที่สนใจนั้นตัดผ่าน $\Delta$ ชิ้นใดบ้าง และจำนวนของ $\Delta$ ที่โดนตัดก็ควรต้องมีขนาดเพียงแค่ $O(\sqrt{r})$ ชิ้น ดังนั้นเราจึงสามารถใช้โครงสร้างข้อมูลอันเดิมนี้ได้ทันทีเลยกับพิสัย $t$ แบบสามเหลี่ยม โดยส่วนที่ต้องปรับก็คืออัลกอริทึมที่จะตรวจเช็คว่าแต่ละ $\Delta$ นั้นอยู่ภายใน $t$ ทั้งหมด/อยู่ภายนอกทั้งหมด/โดนตัดผ่ากลางหรือไม่แค่นั่นเอง

อ้างอิง

• Matoušek, Jiří. “Efficient partition trees.” Proceedings of the seventh annual symposium on Computational geometry. 1991.
• De Berg, Mark, et al. Computational geometry: algorithms and applications. Springer Science & Business Media, 2008.