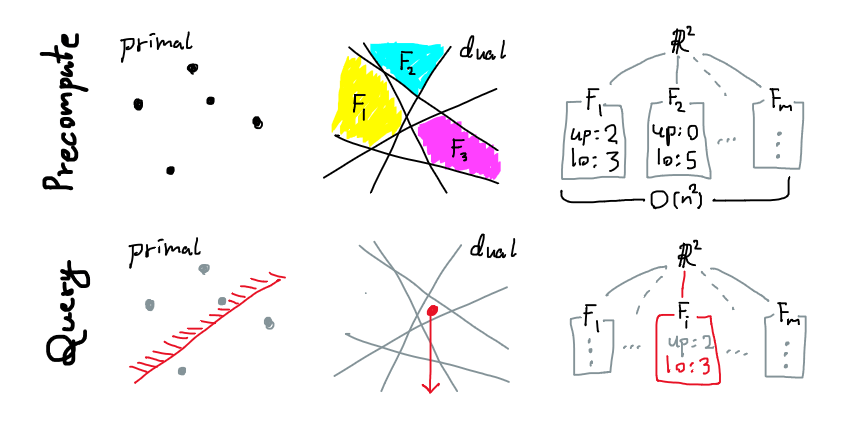ในปัญหาการค้นหาบนพิสัย เราได้เห็นถึงเทคนิคแรกที่แบ่งปัญหาย่อยๆ เป็นซิมเพล็กซ์ไปแล้ว ซึ่งแนวทางดังกล่าวจะให้โครงสร้างสำหรับเก็บข้อมูลขนาดเล็กแต่ก็แลกมากับการใช้เวลาค้นหานาน ในตอนนี้เราจะมาดูอีกเทคนิคหนึ่งซึ่งใช้เวลาค้นหารวดเร็วกว่า แต่ว่าจะไปบวมตรงพื้นที่เก็บข้อมูลที่คำนวณทิ้งไว้ล่วงหน้าแทน

จากข้อมูลเซตตั้งต้นของจุดใน 2 มิติ $S = \lbrace s_1,s_2,\dots,s_n\rbrace$ เราจะเริ่มจากการสืบค้นง่ายๆ ก่อนเช่นเดิม นั่นก็คือพิจารณาพิสัยครึ่งระนาบ $h$ ที่เราจะถามว่า $\abs{S \cap h}$ มีจำนวนจุดเป็นเท่าไหร่? เป้าหมายของเราในตอนนี้ก็คือสืบค้นให้ได้เร็ว (เร็วในเซนส์ของนักวิทย์คอมฯ ก็คือ $O(\log n)$​ หรือเทียบเท่า) เราจะทำอะไรได้บ้าง?

วิธีการที่เรียบง่ายตรงไปตรงมาที่สุด ก็คือการคำนวณการสืบค้นทุกรูปแบบทิ้งไว้ก่อนเลย นั่นก็คือพิจารณาเซต $H$ ซึ่งเป็นเซตของครึ่งระนาบทุกรูปแบบทั้งหมดที่เป็นไปได้ หลังจากนั้นดูว่าสำหรับแต่ละ $h \in H$ นั้นคลุมจุดใน $S$ เป็นจำนวนเท่าไหร่ แล้วก็เก็บคำตอบจำนวนจุดลงโครงสร้างข้อมูลแบบต้นไม้ เรียบร้อยแล้วตอนจะสืบค้นข้อมูลเราก็แค่ท่องลงไปในโครงสร้างข้อมูลเพื่อหยิบคำตอบที่เป็นใบเพียงใบเดียวออกมาตอบได้เลย (เราประหยัดเวลาสืบค้นได้จากการเวียนเกิดลงไปที่ปมเดียวในแต่ละชั้นนี่แหละ)

แน่นอนว่าวิธีข้างต้นนี้เป็นไปไม่ได้ในทางปฎิบัติ เนื่องจากเรามีครึ่งระนาบจำนวนมากมายเป็นอนันต์ อย่างไรก็ตามหากเราสังเกตดีๆ จะเห็นว่ามีครึ่งระนาบหลายอันที่ใกล้เคียงกัน นั่นก็คือครึ่งระนาบเหล่านั้นสามารถคลุมจุดใน $S$ ได้เป็นซับเซตเดียวกันหมดเลย

ตัวอย่างครึ่งระนาบสามอันที่แตกต่างกัน แต่ก็ยังสามารถครอบคลุมซับเซตของจุดที่เหมือนกันได้

ดังนั้นเราอาจจัดกลุ่มพาร์ทิชัน $H$ ด้วยความใกล้เคียงกันของครึ่งระนาบเหล่านั้นก็ได้ แล้วหลังจากนั้นเมื่อเราต้องสืบค้นด้วยครึ่งระนาบ $h$ เราก็แค่เอา $h$ ไปดูว่ามันอยู่ในกลุ่มไหน ดังนั้นคำถามที่ตามมาก็คงหนีไม่พ้นว่า เราแบ่งกลุ่มครึ่งระนาบเหล่านั้นได้เป็นจำนวนเท่าไหร่? และเราจะค้น $h$ ได้ยังไงว่าอยู่กลุ่มไหน?

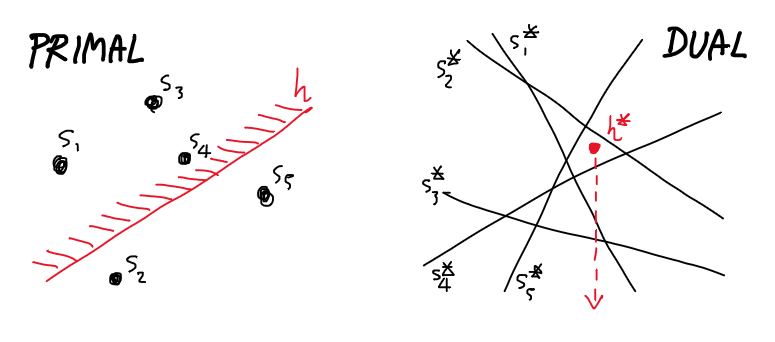
การจะตอบคำถามเหล่านั้นตรงๆ บนปริภูมิตั้งต้นของปัญหานั้นไม่ง่ายเลย แต่มันกลับง่ายลงจนกลายเป็นปัญหาพื้นฐานทันทีเมื่อเรามองปัญหาด้วยแนวคิดทวิภาวะจุด-เส้นตรง ที่เราจะแปลงวัตถุต่างๆ จากปริภูมิตั้งต้น (primal space) ให้กลายเป็นวัตถุในปริภูมิควบคู่ (dual space) นั่นก็คือ แปลงเซตของจุดตั้งต้น $S$ ให้กลายเป็นเซตของเส้นตรง $S^\ast$ และแปลงครึ่งระนาบ $h$ ให้กลายเป็นจุด $h^\ast$ (พร้อมทั้งเก็บทิศทางว่าชี้ขึ้นหรือลง) ดังภาพต่อไปนี้

(ซ้าย) ครึ่งระนาบ $h$ ที่คลุมจุด $s_1,s_3,s_4$ ซีกบน (ขวา) จุด $h^\ast$ ที่ชี้ลงไปโดนเส้น $s_1^\ast,s_3^\ast,s_4^\ast$ ข้างล่าง

สังเกตว่าเส้นตรงจาก $S^\ast$ นั้นตัดแบ่งปริภูมิออกเป็นเซลล์รูปทรงคอนเวกซ์จำนวนมาก ให้ $F_i$ แทนแต่ละเซลล์เหล่านั้น จะเห็นว่าแต่ละ $F_i$ มีสมบัติที่สำคัญก็คือ ไม่ว่าจุด $h^\ast$ จะอยู่ ณ ตำแหน่งใดใน $F_i$ ที่สนใจ จุด $h^\ast$ นั้นจะชี้ขึ้น(หรือลง)ไปโดนเส้นตรงใน $S^\ast$ ชุดเดียวกันทั้งหมดเสมอ ซึ่งก็หมายความว่า แต่ละ $F_i$ ในปริภูมิควบคู่ก็คือการแบ่งกลุ่มของระนาบที่ใกล้เคียงกันในปริภูมิตั้งต้นที่เราต้องการนั่นเอง

เราจึงได้คำตอบแล้วว่ามีครึ่งระนาบอยู่ $O(n^2)$ กลุ่มที่ให้ผลลัพธ์การสืบค้นเดียวกัน (เพราะว่ามีเซลล์ได้เพียงแค่ $O(n^2)$ เซลล์) และการจะบอกว่า $h$ อยู่ในกลุ่มไหนก็เทียบเท่าได้กับการพิจารณาว่า $h^\ast$ ไปตกอยู่ใน $F_i$ ชิ้นใดในปริภูมิควบคู่แทน (ซึ่งทำได้เร็วใน $O(\log n)$ ด้วยเทคนิคสุดพื้นฐาน แต่เราจะเก็บเรื่องนี้ไว้พูดถึงในโอกาสหน้า) นั่นก็คือตอนนี้เราได้อัลกอริทึมและโครงสร้างข้อมูลที่เราต้องการ ที่ใช้เวลาในการสืบค้นเป็น $O(\log n)$ และกินพื้นที่จัดเก็บเป็น $O(n^2)$​ เป็นที่เรียบร้อย

(จากซ้ายไปขวา บนลงล่าง) แนวคิดการทำงานโดยสังเขปสำหรับการสืบค้นด้วยพิสัยครึ่งระนาบ

หมายเหตุ: โครงสร้างข้อมูลที่เราใช้คือต้นไม้มีรากที่มีความลึกเพียงแค่หนึ่งและมีจำนวนใบเป็น $O(n^2)$ ซึ่งอาจดูเป็นการใช้โครงสร้างข้อมูลที่ไม่เหมาะสมนัก แต่มันจะเป็นรากฐานสำหรับทำความเข้าใจปัญหานี้ต่อไป

---

เมื่อเราแก้ปัญหาการสืบค้นด้วยครึ่งระนาบ $h$ ได้แล้ว เราก็อาจถามต่อไปว่าแล้วสำหรับพิสัยอื่นๆ ที่ซับซ้อนกว่านี้หละ เราจะยังใช้วิธีการข้างต้นได้อยู่หรือไม่?

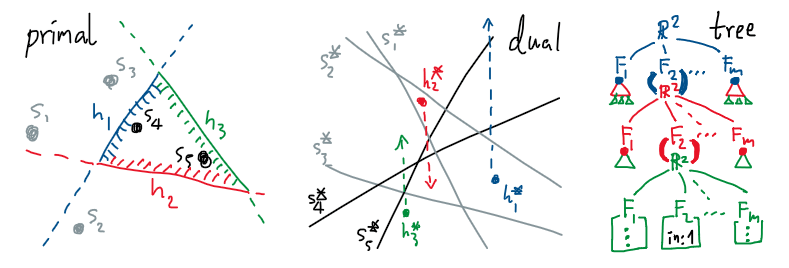
ในที่นี้เราจะแค่พิจารณาแค่การสืบค้นด้วยพิสัยสามเหลี่ยม $t$ ซึ่งมันเป็นพิสัยแบบที่ง่ายรองลงมาจากครึ่งระนาบ เพราะอันที่จริงแล้วมันก็คืออินเตอร์เซกชันกันของครึ่งระนาบจำนวนสามอัน ดังนั้นเราอาจคิดตรงไปตรงมาได้ว่า เราก็แค่แยกส่วนเส้นขอบสามเหลี่ยมให้กลายเป็นครึ่งระนาบ $h_1,h_2,h_3$ แล้วก็แปลงมันต่อเป็นจุดพร้อมทิศทาง $h_1^\ast,h_2^\ast,h_3^\ast$ ในปริภูมิควบคู่ สุดท้ายก็ดูว่าทั้งสามจุดนี้มันชี้ไปโดนเส้นตรงไหนพร้อมกันทั้งหมดใน $S^\ast$ บ้าง

การตีความสามเหลี่ยมในปริภูมิควบคู่พร้อมทั้งโครงสร้างข้อมูลที่ตรงไปตรงมา

ข้อจำกัดสำคัญของแนวคิดข้างต้น คือเราไม่สามารถค้นคำตอบของ $h_1^\ast,h_2^\ast,h_3^\ast$ แยกกันแล้วเอาผลลัพธ์มารวมทีหลังได้ นั่นก็เพราะ

\[\abs{h_1 \cap S} + \abs{h_2 \cap S} + \abs{h_3 \cap S} \ne \abs{h_1 \cap h_2 \cap h_3 \cap S}\]

ถ้าเราจะนำแนวคิดดังกล่าวมาใช้ตรงๆ เราจะต้องค้น $h_1^\ast$ แล้วต่อด้วยค้น $h_2^\ast$ และปิดท้ายด้วยการค้น $h_3^\ast$ อย่างต่อเนื่องกัน นั่นก็คือสำหรับโครงสร้างข้อมูลแล้ว เราต้องซ้อนต้นไม้เข้าไปสามชั้น ซึ่งก็คือเราจะเปลี่ยนใบของต้นไม้ชั้นแรกจากเดิมที่เก็บข้อมูลการสืบค้นด้วย $h_1^\ast$ ให้กลายเป็นต้นไม้สำหรับสืบค้นด้วย $h_2^\ast$ แทน (และเปลี่ยนใบของต้นไม้ $h_2^\ast$ ให้กลายเป็นต้นไม้สำหรับ $h_3^\ast$) ดังนั้น โครงสร้างข้อมูลสำหรับอัลกอริทึมแบบตรงไปตรงมานี้ จึงกินพื้นที่จัดเก็บสูงถึง $O(n^6)$​ เลยทีเดียว

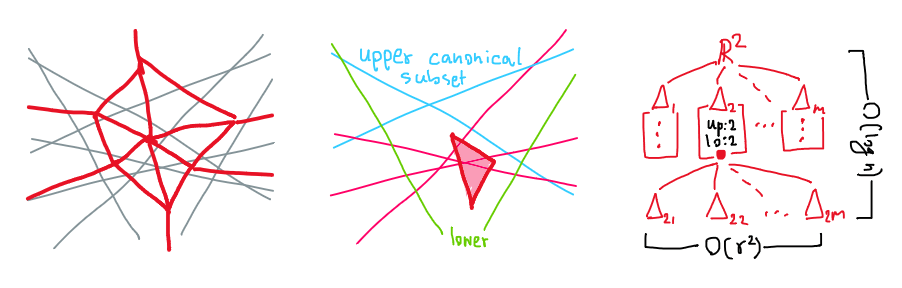
แล้วเราจะประหยัดพื้นที่จัดเก็บข้อมูลกว่านี้ได้หรือไม่? การจะตอบคำถามนี้ให้เข้าใจได้ง่าย จะขอย้อนกลับไปพิจารณากรณีครึ่งระนาบเพียงชิ้นเดียวอีกรอบ ซึ่งเราจะเปลี่ยนไปใช้โครงสร้างข้อมูลแบบ $(1/r)$-ต้นไม้ตัดแบ่ง (cutting tree) ที่มีค่า $r$ เป็นพารามิเตอร์ ซึ่งคราวนี้เราจะตัดแบ่งปริภูมิออกเป็นรูปทรงสามเหลี่ยมปิดหรือเปิดหลายๆ ชิ้นที่แยกออกจากกันโดยเด็ดขาดแทน โดยที่สามเหลี่ยมแต่ละชิ้นจะมีเส้นตรงใน $S^\ast$ พาดผ่านได้ไม่เกิน $n/r$ เส้น ซึ่งจากงานของ Chazelle ในปี 1993 นั้นบอกว่าเราสามารถสร้างต้นไม้ตัดแบ่งที่มีสามเหลี่ยมเพียงแค่ $O(r^2)$ ชิ้นได้ และแน่นอนว่าเมื่อโครงสร้างข้อมูลเป็นแบบต้นไม้ เราก็จะเรียกตัวเองเวียนเกิดลงไปจนกว่าสามเหลี่ยมในชั้นใบจะมีเส้นตรงเพียงแค่เส้นเดียวพาดผ่านมันเท่านั้น

(ซ้าย) เส้นตรงสีเทาจาก $S^\ast$ และโครงสีแดงของ $(1/2)$-ต้นไม้ตัดแบ่ง (กลาง) เมื่อสนใจ $\Delta$ หนึ่งหน้า (ขวา) โครงสร้างข้อมูล

พูดอีกครั้งอย่างรัดกุมก็คือ ต้นไม้ตัดแบ่ง $\Xi(S^\ast) = \lbrace \Delta_1, \Delta_2, \dots, \Delta_m \rbrace$ ที่ดีจะมีขนาดแค่ $m=O(r^2)$ โดยที่แต่ละ $\Delta_i$ นั้นคือสามเหลี่ยมที่อาจไม่ปิดล้อม (เส้นขอบอาจชี้ออกไปยังอนันต์) นอกจากนี้ $\Delta_i$ ต้องมีเส้นตรงจาก $S^\ast$ ไม่เกิน $n/r$ เส้นพาดผ่าน ทั้งนี้ $\Delta_i \cap \Delta_j = \emptyset$ สำหรับทุก $i \ne j$ และ $\bigcap \Delta = \mathbb{R}^2$

อัลกอริทึมสำหรับสืบค้นครึ่งระนาบ $h$ บนโครงสร้างข้อมูลนี้จะยุ่งยากขึ้นเล็กน้อย แต่ใจความจะเหมือนเดิมคือเราจะหาก่อนว่า $h^\ast$ นั้นตกอยู่ใน $\Delta_i$ ชิ้นไหน ซึ่งเราจะเห็นว่า $\Delta_i$ มีเส้นตรงอยู่สูงกว่า/ต่ำกว่ามันอย่างแน่นอนอยู่จำนวนหนึ่ง ทำให้เราสามารถนำจำนวนเส้นตรงกลุ่มนั้นไปบวกเพิ่มในคำตอบของการสืบค้นได้เลย จะเหลือก็เพียงแต่เส้นตรงอีกไม่เกิน $n/r$ เส้นที่พาดผ่าน $\Delta_i$ ที่เราต้องเวียนเกิดเรียกตัวเองลงไปเพื่อชี้ชัดว่ามีเส้นตรงอีกกี่เส้นที่อยู่สูงกว่า/ต่ำกว่าจุด $h^\ast$ นั่นเอง

ด้านเวลาการทำงานของอัลกอริทึม ตรงนี้เราอาจมองง่ายๆ โดยการไล่เช็คทุก $\Delta_i$ จำนวน $O(r^2)$ อันเลยก็ได้ว่า $h^\ast$ อยู่ในนั้นหรือเปล่า ที่เราทำเช่นนี้ได้ก็เพราะว่ามันจะมีเพียง $\Delta_i$ อันเดียวที่เราเวียนเกิดลงไป และความเร็วในการหา $\Delta_i$ ชิ้นที่ถูกต้องนั้นไม่สำคัญเพราะมันเป็นค่าคงที่ (จากพารามิเตอร์ $r$) อยู่ดี ดังนั้น

\[Q(n) = O(r^2) + Q(n/r) \tag{1} \label{eq:recurrent-time-halfplane}\]

การแก้สมการ $\eqref{eq:recurrent-time-halfplane}$ ก็ทำได้ในทำนองเดียวกันกับตอนที่แล้วเลย คือเริ่มจากการถามว่าเราต้องเวียนเกิดลงไปลึกเท่าไหร่ ซึ่งก็คือ $k=\log_rn$ และทำให้เราได้

\[\begin{align} Q(n) &= \overbrace{O(r^2) + O(r^2) + \dots + O(r^2)}^\text{$k$ terms} + O(1) \\ &= O(\log n) \tag{2} \label{eq:time-halfplane} \end{align}\]

ส่วนพื้นที่จัดเก็บที่ใช้นั้นก็ขึ้นกับจำนวนปมของต้นไม้ในแต่ละชั้น ซึ่งเท่ากับ $m=O(r^2)$ โดยที่แต่ละปมก็จะเป็นโครงสร้างต้นไม้ที่สนใจเส้นที่พาดผ่านเหลือเพียง $n_i \le n/r$​ เส้น นั่นก็คือ

\[M(n) = O(r^2) + \sum_{1\le i \le m} M(n_i) \tag{3} \label{eq:recurrent-space-halfplane}\]

ให้ค่าคงที่ $c$ แทนค่าความบวมที่ถูกซ่อนอยู่ภายใต้สัญลักษณ์บิ๊กโอ เราไล่สมการ $\eqref{eq:recurrent-space-halfplane}$ ได้ดังนี้

\[\begin{align} M(n) &= cr^2 + cr^2 \cdot M(n/r) \\ &\le cr^2 \cdot 2M(n/r) \\ &= O( (2cr^2)^k ) \\ &= O( (2c)^k \cdot r^{2k} ) \\ &= O( (2c)^k \cdot n^2 ) \end{align}\]

เราอยากแปลง $(2c)^k$ ให้อยู่ในรูปของ $n^\varepsilon$ ซึ่งก็คือ

\[\varepsilon = \log_r 2c\]

หรือพูดอีกอย่างได้ว่า เราเลือกพารามิเตอร์ $r = (2c)^{1/\varepsilon}$ ที่ทำให้โครงสร้างข้อมูลนี้กินพื้นที่จัดเก็บเป็น

\[M(n) = O(n^{2+\varepsilon}) \tag{4} \label{eq:space-halfplane}\]

จะเห็นว่าสำหรับการสืบค้นด้วยครึ่งระนาบแล้ว อัลกอริทึมบน $(1/r)$-ต้นไม้ตัดแบ่งนี้กินพื้นที่จัดเก็บแย่กว่าการทำงานแบบตรงไปตรงมานิดหน่อย อย่างไรก็ตาม ข้อดีของมันคือการทำให้แต่ละชั้นมีจำนวนปมขึ้นกับพารามิเตอร์ที่เราเลือกได้เอง ซึ่งจะเป็นข้อได้เปรียบมากๆ เมื่อเราต้องซ้อนโครงสร้างข้อมูลเข้าไปในแต่ละปมของต้นไม้ แบบที่เรากำลังจะทำเพื่อแก้ปัญหาการสืบค้นด้วยสามเหลี่ยมนั่นเอง

มาลองนึกถึงอัลกอริทึมสำหรับการสืบค้นด้วยสามเหลี่ยมกันก่อน ในที่นี้สมมติให้สามเหลี่ยมถูกแปลงเป็นครึ่งระนาบ $h_1,h_2,h_3$ ที่ครอบคลุมไปยังซีกล่าง-บน-ล่าง ดังนั้นในปริภูมิควบคู่เราจะมี $h_1^\ast,h_2^\ast,h_3^\ast$ ที่ชี้ไปยังทิศทางขึ้น-ลง-ขึ้น เราจะเริ่มจากถามว่า $h_1^\ast$ อยู่ใน $\Delta_i$ ชิ้นไหน ซึ่งมันจะแบ่งเซตของเส้นตรงใน $S^\ast$ ออกเป็นสามซับเซตให้เราพิจารณาต่อ ดังนี้

1. ซับเซตของเส้นตรงที่อยู่ต่ำกว่า $\Delta_i$ เนื่องจากว่า $h_1^\ast$ ชี้ขึ้น ดังนั้นเส้นตรงกลุ่มนี้จะไม่ถูก $h_1^\ast$ ชี้โดนแน่นอน เราจึงไม่ต้องสนใจมันได้เลย
2. ซับเซตของเส้นตรงที่พาดผ่าน $\Delta_i$ พอดี สำหรับกลุ่มนี้เราไม่แน่ใจว่าจะมีเส้นตรงไหนบ้างที่อยู่สูงหรือต่ำกว่า $h_1^\ast$ เราจึงต้องเรียกตัวเองลงไปโดยเริ่มค้นหาด้วย $h_1^\ast$ ซ้ำอีกครั้ง (บนซับเซตขนาด $n/r$ นี้)
3. ซับเซตของเส้นตรงที่อยู่สูงกว่า $\Delta_i$ ซึ่งเป็นกลุ่มที่เรามั่นใจแน่นอนว่า $h_1^\ast$ ชี้โดน แต่เรายังไม่แน่ใจว่ามันจะถูก $h_2^\ast$ (และ $h_3^\ast$) ชี้โดนด้วยหรือไม่ ดังนั้นเราจึงจะต้องมีโครงสร้างข้อมูลต้นไม้ตัดแบ่งในชั้นถัดไปเพื่อสืบค้นด้วย $h_2^\ast$ (และ $h_3^\ast$) ต่อไป

แน่นอนว่าเราต้องทำแบบนี้ซ้ำกับการค้นด้วย $h_2^\ast$ ที่อาจต้องค้นตัวเองซ้ำในกรณีพาดผ่านพอดี หรือลงไปค้นต่อยังชั้นของ $h_3^\ast$ สำหรับซับเซตของเส้นที่มั่นใจ (แต่จะไม่ถอยกลับไปค้นด้วย $h_1^\ast$ อีกแล้ว)

และท้ายที่สุดเราก็จะทำแบบนี้ซ้ำกับการค้นด้วย $h_3^\ast$ อีกครั้งหนึ่ง เพียงแค่ว่าคราวนี้เราสามารถสรุปได้แล้วว่าเส้นตรงที่เหลือรอดมาให้เรามั่นใจในระดับนี้ จะต้องถูกชี้จาก $h_1^\ast,h_2^\ast,h_3^\ast$ ครบทั้งหมดแน่นอน¹

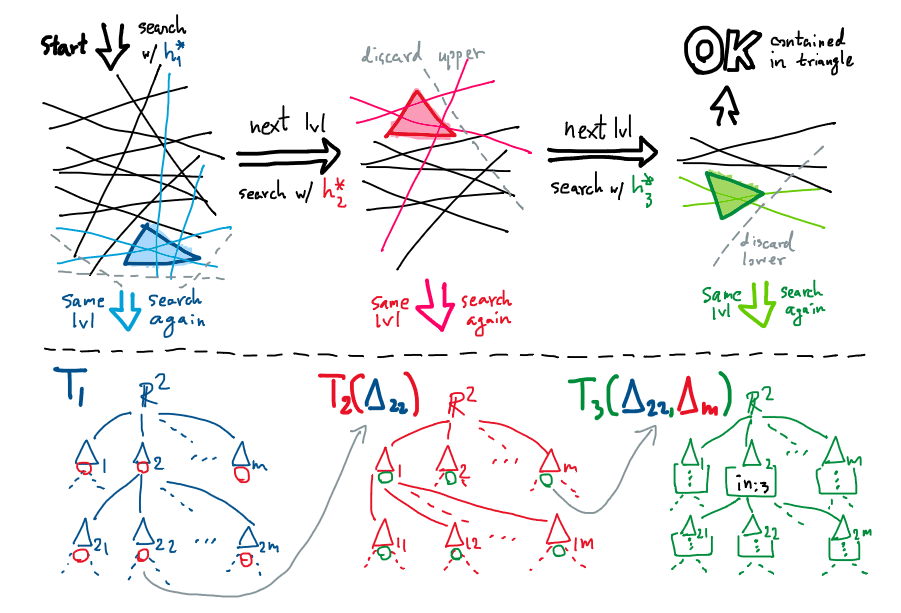
ภาพรวมการสืบค้นพิสัยสามเหลี่ยม (บน) และโครงสร้างข้อมูล (ล่าง) ที่ใช้ $(1/r)$-ต้นไม้ตัดแบ่งสามระดับชั้น

ดังนั้นโครงสร้างข้อมูลที่เราต้องการก็คือต้นไม้ตัดแบ่งที่มีสามระดับชั้น โดยที่ชั้นบนสุด (ที่เราใช้ $h_1^\ast$ ไปสืบค้น) จะมีเพียงแค่ต้นเดียว โดยเราจะเรียกต้นไม้ต้นนี้ว่า $T_1$ ต่อมาต้นไม้ในระดับชั้นถัดที่สองที่จะมีจำนวนมากถึง $O(n^{2+\varepsilon})$ ต้น เนื่องจากแต่ละปมในต้นไม้ $T_1$ จะต้องการเรียกใช้ $T_2$ ที่ไม่เหมือนกัน (จะเขียน $T_2(\Delta_i)$ เพื่อแสดงว่ามันเป็นต้นไม้ระดับชั้น $T_2$ ที่เกิดจากการคำนวณต่อจาก $\Delta_i$ ของ $T_1$) และท้ายที่สุดเราจะมี $T_3$ อีกได้มากถึง $O((n^{2+\varepsilon})^2)$​ ต้นเลยทีเดียว … นี่ยังไม่นับว่า $T_3$ หนึ่งต้นก็มีขนาดใหญ่ได้ถึง $O(n^{2+\varepsilon})$ อีกด้วย

ดูเผินๆ แล้วอาจคิดว่าโครงสร้างข้อมูลนี้ใช้พื้นที่จัดเก็บได้แย่กว่าเดิมเสียอีก แต่อย่าลืมว่าต้นไม้แต่ละต้นนั้นมีขนาดไม่เท่ากัน ต้นไม้ที่โดนสืบค้นลึกๆ นั้นอาจมีขนาดเล็กมากจนแทบไม่ส่งผลกับพื้นที่จัดเก็บก็ได้

เพราะงั้นเราจะมาคำนวณกันอย่างละเอียด โดยเริ่มจากต้นไม้ระดับชั้นล่างสุดที่ $T_3$ สมมติเราสนใจต้นไม้หนึ่งต้นที่ต้องจัดการกับเส้นตรงจำนวน $n$ เส้น เราสามารถตอบได้ทันทีเลยว่าพื้นที่จัดเก็บของต้นไม้ต้นนี้คือ $M_3(n) = O(n^{2+\varepsilon})$ ด้วยการวิเคราะห์แบบเดียวกับสมการ $\eqref{eq:space-halfplane}$ ได้เลย (อนึ่ง เราจะยังไม่กังวลว่าพื้นที่จัดเก็บต้นไม้ $T_3$ เพียงแค่ต้นเดียวนี้มันสูง เพราะต้นไม้ที่ระดับนี้ส่วนใหญ่มีเส้นตรงน้อยกว่า $n$ เส้นมากๆ)

สำหรับระดับชั้นถัดมาที่ $T_2$ เราจะได้ว่าพื้นที่จัดเก็บคือ

\[\begin{align} M_2(n) &= \sum_{1\le i\le m} \left( M_3(n) + M_2(n_i) \right) \\ &= \sum_{1\le i\le m} \left( O(n^{2+\varepsilon}) + M_2(n/r) \right) \\ &= O(r^2)O(n^{2+\varepsilon}) + O(r^2)M_2(n/r) \\ &= O(r^2)O(n^{2+\varepsilon}) + O(r^4)O((n/r)^{2+\varepsilon}) + O(r^4)M_2(n/r^2) \\ &\;\;\vdots \\ &= O\left( r^2n^{2+\varepsilon} \right) + O\left( r^4\left(\frac{n}{r}\right)^{2+\varepsilon} \right) + O\left( r^6\left(\frac{n}{r^2}\right)^{2+\varepsilon} \right) + \dots + O\left( r^{2k}\left(\frac{n}{r^{k-1}}\right)^{2+\varepsilon} \right) \\ &= O(kr^2 \cdot n^{2+\varepsilon}) \end{align}\]

แน่นอนว่าเมื่อสมการอยู่ในรูปประมาณนี้แล้ว เราสามารถละลายส่วนที่เป็น $kr^2$ ให้เข้าไปหลอมรวมกับ $n^\varepsilon$ ได้ (นั่นคือ เราไม่อยากจะเวียนเกิดลงไปลึก โดยเราจะเลือกพารามิเตอร์ $r$ ให้ใหญ่เป็นเงาตามตัวของ $n$ นั่นเอง) ดังนั้นเราจึงอาจมองว่าพื้นที่จัดเก็บสำหรับต้นไม้ $T_2$ หนึ่งต้นก็คือ $M_2(n) = O(n^{2+\varepsilon})$ ได้เช่นกัน

และท้ายสุดสำหรับ $T_1$ เราก็สามารถวิเคราะห์และสรุปในทำนองเดียวกันกับการวิเคราะห์ที่ผ่านๆ มาได้เลยว่ามันจะกินพื้นที่จัดเก็บเท่ากันที่ $M_1(n) = O(n^{2+\varepsilon})$ นั่นเอง

แล้วด้านเวลาการสืบค้นนั้นเป็นยังไง? อันนี้ใช้โครงของการวิเคราะห์สามระดับชั้นได้เช่นเดียวกัน คือเริ่มจากระดับล่างสุดที่ค้นด้วย $h_3^\ast$ ที่จะได้เวลาสืบค้นเป็น $Q_3(n) = O(\log n)$ ตามการวิเคราะห์ $\eqref{eq:time-halfplane}$ ได้เลย

ทีนี้พอย้อนกลับขึ้นมาที่การค้นด้วย $h_2^\ast$ จะได้ว่า

\[\begin{align} Q_2(n) &= O(r^2) + Q_2(n/r) + Q_3(n) \\ &= O(k \cdot r^2) + \left( Q_3(n) + Q_3(n/r) + Q_3(n/r^2) + \dots + Q_3(n/r^k) \right) \\ &= O(k \cdot r^2) + O(k \cdot \log n) \\ &= O(r^2 \log n) + O(\log^2 n) \end{align}\]

หรือก็คือ $Q_2(n) = O(\log^2 n)$ และแน่นอนว่าในท้ายที่สุด เมื่อเราพิจารณาการเริ่มสืบค้นตั้งแต่ $h_1^\ast$ จากระดับชั้นบนสุด เราก็จะเห็นว่ามันใช้เวลาเป็น $Q_1(n) = O(\log^3 n)$ นั่นเอง

อ้างอิง

• Chazelle, Bernard. “Cutting hyperplanes for divide-and-conquer.” Discrete & Computational Geometry 9.2 (1993): 145-158.
• De Berg, Mark, et al. Computational geometry: algorithms and applications. Springer Science & Business Media, 2008.