แบบฝึกหัดสุดคลาสสิกในวิยุตคณิต สนใจปริภูมิ $\mathbb{R}^2$ ถามว่าเส้นตรง $n$ เส้นสามารถตัดแบ่งปริภูมินี้ออกเป็นชิ้นส่วนได้เป็นจำนวนมากที่สุดกี่ชิ้น?

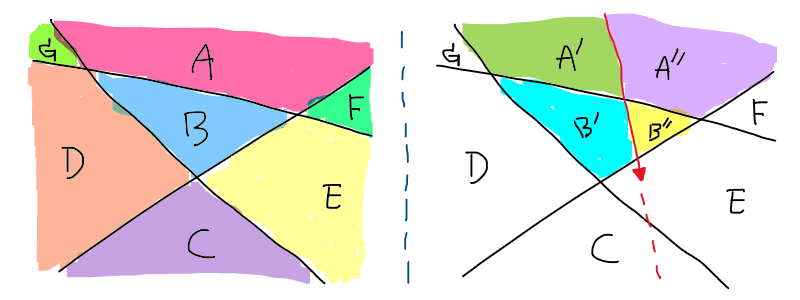
(ซ้าย) เส้นตรงสามเส้นตัดระนาบเป็น 7 ชิ้น (ขวา) ระหว่างที่กำลังลากเส้นตรงเพิ่มเข้าไป

เพื่อความกระจ่าง ชิ้นส่วนหนึ่งชิ้นในที่นี้หมายถึงรูปหลายเหลี่ยม (polygon) ที่มีอาณาบริเวณภายในเชื่อมต่อกันไม่ถูกแบ่งแยกด้วยเส้นตรงใดๆ ซึ่งให้ผลลัพธ์เป็นรูปหลายเหลี่ยมแบบคอนเวกซ์ (convex polygon) เสมอ แต่ว่ามันอาจมีขอบเขตที่ไม่จำกัด (unbounded) ก็ได้ นอกจากนี้จะขอใช้สัญลักษณ์ $\overline{\binom{n}2}$ สำหรับคำตอบจำนวนชิ้นส่วนที่มากที่สุดที่สามารถเกิดได้จากเส้นตรง $n$ เส้นในสองมิติ¹

โดยการตัดให้ได้ชิ้นส่วนมากที่สุดก็คือต้องไม่มีสามเส้นตรงใดๆ ตัดกันที่จุดเดียวกัน (นั่นคือชิ้นส่วนตรงกลางจะไม่หดหายกลายเป็นจุด) ดังนั้นเราสามารถอาศัยการอุปนัยมาพิสูจน์ได้ง่ายๆ ว่าจำนวนชิ้นส่วนจะมีมากที่สุดเท่ากับ

\[\overline{\binom{n}2} = T(n) + 1\]

โดยที่ $T(n)$ คือจำนวนสามเหลี่ยม ซึ่งคำนวณได้จาก $T(n) = 1 + 2 + 3 + \dots + n$

พูดอย่างรัดกุมได้ว่า ให้ $P(n)$ แทนข้อความ “เส้นตรง $n$ เส้นตัดแบ่งปริภูมิได้ $T(n)+1$ ชิ้น” เราจะเริมที่ $P(0)$ ซึ่งเห็นได้ทันทีว่าจริง เพราะในเมื่อไม่มีเส้นมาตัดก็จะได้ปริภูมิทั้งก้อนนับเป็นหนึ่งชิ้น หลังจากนั้นเราจะอุปนัยลงไปโดยสมมติให้ $P(k)$ จริง ซึ่งก็คือเราเริ่มจากการมีชิ้นส่วนอยู่แล้ว $T(k)+1$ ชิ้น ดังนั้นเราต้องการลากเส้นตรง $\ell$ ซึ่งเป็นเส้นตรงเส้นใหม่ให้ไปตัดเส้นตรงอื่นๆ ที่มีอยู่เดิมทั้งหมด สังเกตว่าแต่ละครั้งที่เราลาก $\ell$ ไปชนกับเส้นตรงเดิมแต่ละเส้น เราจะแบ่งชิ้นส่วนที่มีอยู่เดิมได้หนึ่งครั้ง (ยกเว้นครั้งสุดท้ายที่ $\ell$ วิ่งออกไปยังอนันต์ ซึ่งก็คือเราแบ่งชิ้นส่วนชิ้นสุดท้ายที่ไม่จำกัดขอบเขตได้อีกหนึ่งครั้งเช่นกัน) ดังนั้นจำนวนชิ้นส่วนทั้งหมดหลังจากเพิ่ม $\ell$ เข้าไป (จนมีเส้นตรงรวมเป็น $k+1$ เส้น) ก็คือ

\[\overline{\binom{k}2} + k + 1 = T(k) + 1 + k + 1 = T(k+1) + 1 = \overline{\binom{k+1}2}\]

นั่นก็คือ $P(k+1)$ เป็นจริงด้วย และทำให้สรุปได้ว่า $P(n)$ ทั้งหมดจริง

อนึ่ง ปัญหานี้เป็นที่รู้จักอีกชื่อว่า ลำดับตัวเลขของร้านจัดเลี้ยงแสนขี้เกียจ เพราะเค้าเปรียบเทียบกับร้านจัดเลี้ยงอาหารนอกสถานที่ ที่หั่นพิซซ่าที่เฉไปเฉมาไม่ชนกันตรงกลางพอดี เพื่อที่จะแบ่งพิซซ่าหนึ่งถาดให้ได้จำนวนมากที่สุด (แทนที่จะต้องไปอบพิซซ่าเพิ่มนั่นเอง)

---

คำถามที่น่าสนใจก็คือ แล้วถ้าเราเปลี่ยนไปสนใจ $\mathbb{R}^3$ บ้างหล่ะ? นั่นคือเราจะเปลี่ยนไปใช้ระนาบ $n$ ระนาบมาแบ่งปริภูมิแทน แล้วจำนวนชิ้นส่วน (คราวนี้คือนับ $\overline{\binom{n}3}$ บนทรงหลายหน้า (polyhedron) แทนแล้ว) ที่ถูกตัดแบ่งจะมีจำนวนได้มากที่สุดได้เท่าไหร่

สี่ระนาบตัดปริภูมิ ก่อให้เกิดชิ้นส่วนทรงหลายหน้าจำนวน 15 ชิ้น ภาพจาก Wikipedia

แม้ปัญหาในสามมิติจะยังอยู่ในวิสัยพอให้มองภาพได้ แต่ส่วนที่มันทับซ้อนกันก็เริ่มจะซับซ้อนเกินกว่าจะจินตนาการตามทันแล้ว กอปรกับเทคนิคการลากเส้นในสองมิติก็ไม่สามารถนำมาประยุกต์ใช้ได้อีกต่อไป เพราะงั้นเราควรต้องมองหาเทคนิคใหม่ๆ เพื่อนำมาใช้แก้ปัญหานี้ (อันที่จริง ถ้าคิดไม่ออก ลองไล่กรณีง่ายๆ เพื่อดูแพทเทิร์นตัวเลขก็ไม่เลวนะ…)

แล้วเทคนิคไหนที่เราควรใช้? สังเกตว่าเราใช้ระนาบสองมิติเข้าไปตัดปริภูมิสามมิติ ดังนั้นเราอาจลองหยิบระนาบ $\phi$ ที่เอาไปตัดระนาบอื่นๆ มาดูร่องรอยบนตัวมันก็พอ ซึ่งจะเห็นได้ทันทีว่า

• รอยเส้นตรงหนึ่งเส้นที่ปรากฏบน $\phi$ ในสองมิติ แท้จริงแล้วมันก็คือระนาบชิ้นอื่นที่มาตัดเฉียงๆ กับ $\phi$ ในสามมิตินั่นเอง
• ชิ้นส่วนหนึ่งชิ้นที่เป็นรูปหลายเหลี่ยมบน $\phi$ ในสองมิติ มันต้องเกิดจากชิ้นส่วนที่เป็นทรงหลายหน้าในสามมิติที่ถูกตัดด้วย $\phi$ เป็นแน่แท้ (พูดอีกอย่างก็คือ ระนาบ $\phi$ ตัดทรงหลายหน้าจากหนึ่งชิ้นให้กลายเป็นสองชิ้นบนล่าง โดยมีหน้าใหม่ที่แบ่งครึ่งทรงหลายหน้าคือรูปหลายเหลี่ยมบน $\phi$ นั่นเอง)

นั่นก็คือ การเพิ่มระนาบใหม่หนึ่งระนาบเข้าไปยังระบบเดิมที่มี $n-1$ ระนาบอยู่ก่อน จำนวนของชิ้นส่วนทรงหลายหน้าที่เพิ่มขึ้นมาในขั้นตอนนี้จะเท่ากับ $\overline{\binom{n-1}2}$ ชิ้นส่วน ดังนั้นโดยการอุปนัยก็จะทำให้เราสรุปได้ว่าจำนวนชิ้นส่วนทั้งหมดก็คือ

\[\overline{\binom{n}3} = \overline{\binom{n-1}3} + \overline{\binom{n-1}2}\]

ลำดับตัวเลขนี้มีอีกชื่อหนึ่งว่าตัวเลขเค้ก ซึ่งน่าจะมาจากการตั้งชื่อล้อไปกับปัญหาสองมิติข้างต้น เพียงแต่ว่าในสามมิติที่ให้เป็นเค้กก็คงเพราะว่าการตัดเฉียงๆ บนชิ้นส่วนที่มีความกว้างยาวสูงนั้น ให้ผลลัพธ์ที่แตกต่างจากการตัดพิซซ่าที่แบนราบเหมือนเป็นสิ่งของในสองมิติหละมั้ง

---

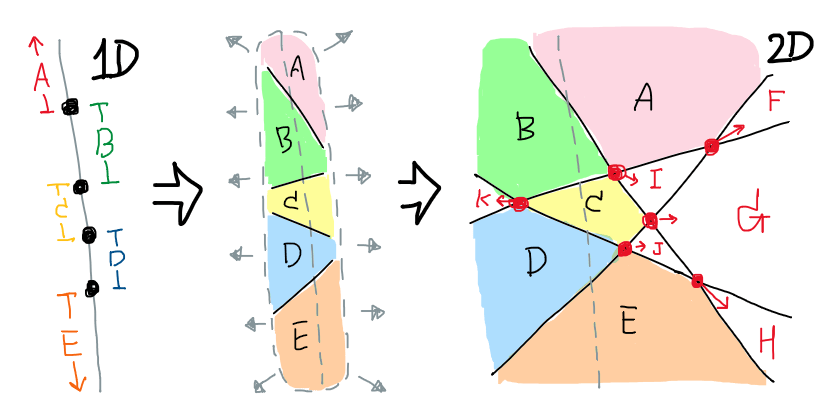
ความเจ๋งของเทคนิคข้างต้นในสามมิติก็คือ มันทำให้เราเกิดสหัชญาณเกี่ยวกับการอธิบายการเกิดชิ้นส่วนชิ้นใหม่ได้อย่างเป็นระบบระเบียบ ซึ่งก็คือเราไม่ได้สนใจความสัมพันธ์ของระนาบชิ้นใหม่กับระนาบเดิมเสียทีเดียว แต่เราสนใจความสัมพันธ์ของภาพฉายของชิ้นส่วนที่ถูกระนาบใหม่นี้ตัดเข้าไปต่างหาก ซึ่งเราสามารถเอาไปปรับปรุงคำอธิบายกรณีการเพิ่มเส้นเข้าไปในระนาบสองมิติได้ด้วย นั่นคือมองเส้นตรงหนึ่งเส้น (มองแบบเส้นจำนวน) แล้วนับว่ามีช่วง (interval) ที่ถูกคั่นด้วยจุดเป็นจำนวนกี่ช่วง (แต่ละจุดแท้จริงแล้วคือเส้นตรงเส้นอื่นๆ นั่นแหละ) ด้วยคำอธิบายที่ถูกปรับปรุงนี้ เราได้

\[\overline{\binom{n}2} = \overline{\binom{n-1}2} + \overline{\binom{n-1}1}\]

แน่นอนว่าเราสามารถใช้คำอธิบายนี้อธิบายย้อนกลับลงไปที่หนึ่งมิติ (หรือแม้กระทั่งศูนย์มิติ) ได้อีกด้วย และทำให้ได้สมการในทำนองเดียวกันออกมาว่า

\[\overline{\binom{n}d} = \overline{\binom{n-1}d} + \overline{\binom{n-1}{d-1}} \tag{1} \label{eq:add-prev}\]

เมื่อ $d$ เป็นจำนวนมิติที่ไม่น้อยกว่าศูนย์ (เพื่อความสะดวก กำหนด $\overline{\binom{n}d}=0$ เมื่อ $d$ ติดลบไปเลยก็ได้)

นอกจากนี้ สมการ $\eqref{eq:add-prev}$ ยังมีความเรียบง่ายสวยงามชวนให้เรานึกถึงสามเหลี่ยมปัสกาลอีกด้วย น่าเสียดายว่าพอเราลองไล่เติมค่าลงในตารางดูแล้ว มันกลับไม่ใช่สามเหลี่ยมปัสกาลไปซะได้

\[\begin{array}{c|cc} n \backslash d & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 1 & \color{lightgray}1 & \color{lightgray}1 & \color{lightgray}1 & \color{lightgray}1 \\ 1 & 1 & 2 & \color{lightgray}2 & \color{lightgray}2 & \color{lightgray}2 \\ 2 & 1 & 3 & 4 & \color{lightgray}4 & \color{lightgray}4 \\ 3 & 1 & 4 & 7 & 8 & \color{lightgray}8 \\ 4 & 1 & 5 & 11 & 15 & 16 \\ 5 & 1 & 6 & 16 & 26 & 31 \end{array}\]

ตารางตัวอย่างค่า $\overline{\binom{n}d}$

อย่างไรก็ตาม หากเราจับคู่สองช่องแนวนอนที่ติดกัน แล้วเอาช่องขวามาลบช่องซ้าย จะเห็นทันทีว่า

\[\begin{array}{c|cc} n \backslash d & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 1 & \color{lightgray}0 & \color{lightgray}0 & \color{lightgray}0 & \color{lightgray}0 \\ 1 & 1 & 1 & \color{lightgray}0 & \color{lightgray}0 & \color{lightgray}0 \\ 2 & 1 & 2 & 1 & \color{lightgray}0 & \color{lightgray}0 \\ 3 & 1 & 3 & 3 & 1 & \color{lightgray}0 \\ 4 & 1 & 4 & 6 & 4 & 1 \\ 5 & 1 & 5 & 10 & 10 & 5 \end{array}\]

ตารางตัวอย่างค่า $\overline{\binom{n}d} - \overline{\binom{n}{d-1}}$

จึงทำให้เราคาดการณ์ได้ว่า

\[\overline{\binom{n}d} - \overline{\binom{n}{d-1}} = \binom{n}{d} \tag{2} \label{eq:sub-prev}\]

แล้วเราจะรู้ได้อย่างไรว่าสมการ $\eqref{eq:sub-prev}$ ถูก? ทางหนึ่งที่อาจทำได้ก็คืออุปนัยสองชั้นโดยให้ชั้นนอกเป็นตัวแปรที่วิ่งบนมิติ $d$ และชั้นในเป็นตัวแปรวิ่งบนจำนวนวัตถุ $n$ ต่อไปนี้จะขอข้ามกรณีพื้นฐานง่ายๆ ในตอนต้นของการอุปนัย แล้วกระโดดมาสนใจสมมติฐานเลยว่า

\[\overline{\binom{k}d} - \overline{\binom{k}{d-1}} = \binom{k}{d}\]

ในการอุปนัยสองชั้นเช่นนี้ เราได้พิสูจน์ชั้นนอกในมิติที่ต่ำกว่าเสร็จเรียบร้อยไปก่อนหน้าแล้ว นั่นก็คือเรามั่นใจในกรณีที่ว่า $\overline{\binom{k}{d-1}} - \overline{\binom{k}{d-2}} = \binom{k}{d-1}$ และเมื่อนำความรู้นี้ไปใช้ควบคู่กับสมการ $\eqref{eq:add-prev}$ ก็จะได้

\[\begin{align} \left( \overline{\binom{k}d} + \overline{\binom{k}{d-1}} \right) - \left( \overline{\binom{k}{d-1}} + \overline{\binom{k}{d-2}} \right) &= \binom{k}{d} + \binom{k}{d-1} \\ \overline{\binom{k+1}d} - \overline{\binom{k+1}{d-1}} &= \binom{k+1}{d} \end{align}\]

นั่นคือเรายืนยันข้อคาดการณ์ $\eqref{eq:sub-prev}$ และจะทำให้ได้ผลลัพธ์ต่อเนื่องตามมาว่า

\[\begin{align} \overline{\binom{n}0} &= \binom{n}0 \\ \overline{\binom{n}1} &= \binom{n}1 + \binom{n}0 \\ \overline{\binom{n}2} &= \binom{n}2 + \binom{n}1 + \binom{n}0 \\ \overline{\binom{n}3} &= \binom{n}3 + \binom{n}2 + \binom{n}1 + \binom{n}0 \end{align}\]

หรือก็คือ

\[\overline{\binom{n}d} = \binom{n}d + \dots + \binom{n}2 + \binom{n}1 + \binom{n}0 \tag{3} \label{eq:bernoulli}\]

ซึ่งจริงๆ แล้วสมการ $\eqref{eq:bernoulli}$​ นี่มันก็คือนิยามสามเหลี่ยมแบร์นุลลีเลยนั่นแหละ โดยเราสามารถตีความแต่ละพจน์ได้เช่นนี้ (จะขอยกตัวอย่างที่ $d=3$ นั่นคือ นำวัตถุที่เป็นแผ่นระนาบ $\lbrace \phi_1,\phi_2,\dots,\phi_n \rbrace$ ไปตัดปริภูมิ $\mathbb{R}^3$)

• $\binom{n}0$ ไม่เลือกระนาบแผ่นไหนเลย จึงได้เป็นปริภูมิทั้งอัน
• $\binom{n}1$ เลือกระนาบทีละแผ่น นั่นคือจะได้แต่ละระนาบ $\phi$
• $\binom{n}2$ เลือกระนาบทีละสองแผ่น นั่นคือจะได้เส้นตรง $\phi_i\cap\phi_j$
• $\binom{n}3$ เลือกระนาบทีละสามแผ่น นั่นคือจะได้จุด $\phi_i\cap\phi_j\cap\phi_k$

เพราะงั้นคำอธิบายก็คือ จำนวนชิ้นส่วนที่ตัดได้ทั้งหมด จะเท่ากับผลรวมของวิธีการเลือกวัตถุแผ่นระนาบ ตั้งแต่เลือกครั้งละศูนย์ระนาบไปจนถึง $d$ ระนาบนั่นเอง (เลือกมากกว่าขนาดมิติไม่ได้ ไม่งั้นจะได้เซตว่าง)

ทำไมถึงอธิบายแบบนี้ได้? เราอาจใช้การอุปนัยมาตอบได้อีกเช่นกัน เพียงแต่คราวนี้เราจะตรึงจำนวนระนาบ $n$ แผ่นเป็นค่าคงตัวใน $\mathbb{R}^3$ แล้วอุปนัยบนตัวแปรมิติ $d$ แทน โดยในแต่ละขั้นที่เราอุปนัย เราจะพิจารณาระนาบว่าถูกฉายลงมาเป็นวัตถุแบบ $d-1$ มิติ

เราเริ่มที่ $d=0$ ซึ่งก็คือพิจารณาปริภูมิ $\mathbb{R}^0$ หรือก็คือปริภูมิที่เป็นจุด พูดอีกอย่างก็คือเราจะเลือกจุดใดจุดหนึ่งในปริภูมิ $\mathbb{R}^3$ ที่ไม่ได้อยู่บนระนาบ $\phi$ ใดๆ มาก็ได้ ดังนั้นเราได้ว่าภาพฉายของทุก $\phi$ จะไม่ปรากฏเลย ดังนั้นจุดที่เราเลือกมานี้จะต้องไปอยู่ในชิ้นส่วนใดชิ้นส่วนหนึ่ง ดังนั้นจึงนับได้ว่ามีชิ้นส่วนที่เราเคยเห็นแล้ว $\binom{n}0$ ชิ้น

ต่อมาที่ $d=1$ เราจะยืดปริภูมิ $\mathbb{R}^0$ ในตอนที่แล้วไปเป็นปริภูมิ $\mathbb{R}^1$ ซึ่งมันจะวิ่งชนกับ $\phi$ ต่างๆ ที่มีภาพฉายเป็นจุดเป็นจำนวน $\binom{n}1$ ครั้ง ดังนั้นแต่ละครั้งที่วิ่งชนจุด เราก็จะให้จุดนั้นรับผิดชอบชิ้นส่วนที่มองเห็นใหม่ไปเลยนั่นเอง ดังนั้นรวมแล้วถึงตอนนี้เราจะเห็นชิ้นส่วนทั้งหมด $\binom{n}0+\binom{n}1=\overline{\binom{n}1}$ ชิ้น

ถัดมา $d=2$ ยืด $\mathbb{R}^1$ เป็น $\mathbb{R}^2$ นั่นหมายความว่าเราต้องยืดแต่ละภาพฉายของ $\phi$ ที่เคยเป็นจุดให้กลายเป็นเส้นด้วย (เราอาจทดลองคิดนอกรอบว่า ช่วงแรกที่เรายืดปริภูมินั้น ทุก $\phi$ ยังไม่วิ่งไปตัดกันก็ได้ ซึ่งจะเห็นว่าเรายังนับชิ้นส่วนได้จำนวนเท่าเดิม) แต่เนื่องจากไม่มี $\phi$ ใดเลยที่ขนานกัน เราจะได้ว่าแต่ละคู่ของเส้น $\phi_i,\phi_j$ จะตัดกันที่จุด $\phi_i\cap\phi_j$ ซึ่งมีจำนวนทั้งหมด $\binom{n}2$ จุด และนอกจากจุดตรงนั้นเราก็จะเห็นชิ้นส่วนชิ้นใหม่ที่ไม่เคยโดนนับอีกด้วย เพราะงั้นเราจะให้แต่ละจุดเหล่ารับผิดชอบชิ้นส่วนหนึ่งชิ้นที่โผล่ขึ้นมาเมื่อพิจารณา $\mathbb{R}^2$ นี้เอง และทำให้ได้ว่ารวมมีชิ้นส่วนทั้งหมด $\overline{\binom{n}2}$ ชิ้น

ท้ายสุด $d=3$ เราจะทำเช่นเดิมคือยืด $\mathbb{R}^2$ ไปเป็น $\mathbb{R}^3$ ที่จะทำให้ได้ว่าเราต้องยืดภาพฉายแต่ละแบบของ $\phi$ ด้วย ซึ่งได้แก่ ยืดเส้นเป็นระนาบ, ยืดจุดเป็นเส้น และสร้างจุดในชั้นนี้เพิ่มขึ้นมาจาก $\phi_i\cap\phi_j\cap\phi_k$ ซึ่งมี $\binom{n}3$ จุด แน่นอนว่าแต่ละจุดเหล่านี้จะรับผิดชอบชิ้นส่วนใหม่ที่ยังไม่เคยโดนนับเมื่อพิจารณาปริภูมินี้ และทำให้สรุปได้ว่าสุดท้ายจะมีชิ้นส่วนทั้งหมด $\overline{\binom{n}3}$ ชิ้น

ตัวอย่างการขยายปริภูมิจาก $\mathbb{R}^1$ ไป $\mathbb{R}^2$ และความรับผิดชอบของแต่ละจุด $\phi_i\cap\phi_j$ ต่อชิ้นส่วนใหม่ที่เพิ่งมองเห็น

อนึ่งก็คือในมิติสูงๆ ขึ้นไป (ที่จินตนาการตามไม่ออกแล้ว) ไม่รู้ว่าจะยังใช้คำอธิบายในแนวทางนี้ได้อยู่หรือเปล่านะ (ก็คงได้แหละ ถ้าเชื่อในผลลัพธ์สมการสวยๆ เหล่านั้น 😂) แต่สำหรับ $\overline{\binom{n}4}$ นี้มันมีวิธีตีความได้อีกทางนึงไปเลย นั่นคือเรายังคงสนใจจำนวนชิ้นส่วนมากที่สุดที่สามารถตัดแบ่งได้เหมือนเดิม แต่เปลี่ยนกฏเป็นว่าเริ่มจากจุด $n$ จุดบนขอบวงกลมแทน แล้วค่อยแบ่งชิ้นส่วนด้วยการลากเส้นตรงเชื่อมทุกคู่จุดเหล่านั้น โดยมันจะให้ผลลัพธ์เป็นชุดตัวเลขลำดับหลอกลวง 1, 2, 4, 8, 16, 31 ที่เราคุ้นเคยกันดีนั่นเอง 😂😂