ตอนเรียนเรื่องการนับและการจัดหมู่ครั้งแรก เห็นนิยาม $n!$ กับ $n!/r!$ แล้วก็ไม่ได้ตะหงิดติดใจอะไร แต่พอมาถึง $\binom{n}{r}=n!/r!(n-r)!$ แล้วแอบคาใจแปลกๆ ว่าทำไมตัวเลขตัวนี้ถึงเป็นจำนวนเต็มได้ … แน่นอนหละว่ามันเป็นการนับ ยังไงซะเราคงไม่นับสิ่งที่สนใจด้วยเลขที่ไม่ใช่จำนวนเต็มเป็นแน่ แต่มันจะมีวิธีการพิสูจน์แบบอื่นที่อธิบายได้รัดกุม ขจัดปัดเป่าข้อข้องใจนี้ทิ้งไป ไม่ชวนให้กลับมาสงสัยซ้ำๆ ในอนาคตมั้ย?

ผ่านมาน่าจะเกินสิบปี จู่ๆ ก็นึกวิธีพิสูจน์ที่ฟังดูเข้าท่า (อย่างน้อยก็กับตัวเอง) ที่ทำได้ผ่านการอุปนัยสองชั้น (double induction) ออก ซึ่งนี่เป็นท่าที่เจ๋งดีเวลาต้องการพิสูจน์บนตัวแปรหลายตัว

---

แต่ก่อนอื่น จะขอแนะนำสัญลักษณ์ที่ใช้งานได้สะดวกในเรื่องการนับ นั่นคือแฟคทอเรียลขาขึ้น $x^\overline{n}$ โดยหลักการทำงานของมันก็คล้ายกับแฟคทอเรียลธรรมดาที่คูณจำนวนนับที่อยู่ติดกันขึ้นไปเรื่อยๆ เป็นจำนวน $n$ ตัวนั่นแหละ เพียงแต่ว่าเลขตัวแรกในผลคูณมันไม่จำเป็นต้องเริ่มที่หนึ่งเท่านั้น แต่สามารถเริ่มที่จำนวนเต็มบวก $x$ ใดๆ ก็ได้ ซึ่งก็คือ

\[x^\overline{n} = \prod_{i=0}^{n-1} (x+i) = x (x+1) (x+2) \cdots (x+n-1)\]

นั่นก็คือ $1^\overline{n} = n!$ โดยมีข้อสังเกตสำคัญคือ เมื่อ $n=0$​ เราจะได้ผลคูณว่าง ซึ่งมันควรจะมีค่าเป็นเอกลักษณ์การคูณนั่นเอง

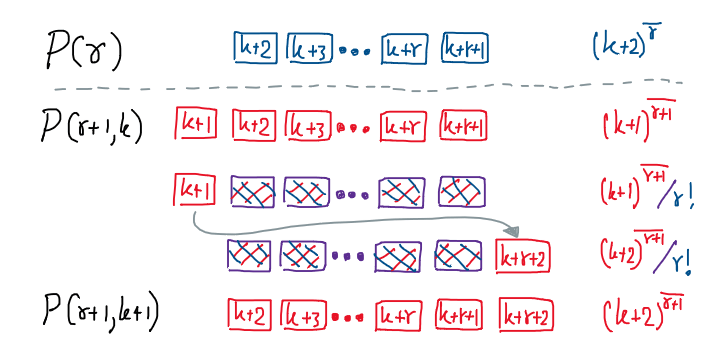
โครงร่างอย่างสังเขปสำหรับการพิสูจน์ด้วยอุปนัยสองชั้นในโจทย์ข้อนี้

กลับมาสนใจปัญหาหลักที่เราต้องการพิสูจน์ว่า $\binom{n}{r}$ เป็นจำนวนนับ ให้ $n=r+k$ โดยที่ $r,k\in\mathbb{N}$ ดังนั้น

\[\binom{n}{r} = \binom{r+k}{r} = \frac{(k+1)^\overline{r}}{r!}\]

หรือก็คือเราสามารถเปลี่ยนปัญหาดังกล่าวไปเป็นปัญหาที่ทัดเทียมกันได้ว่า “$r!$ หารลงตัว¹กับผลคูณของจำนวนธรรมชาติที่เขียนติดกัน $r$ ตัว” นั่นก็คือเราต้องการพิสูจน์ว่า

\[\forall r \forall k\left[ r! \;\Big\vert\; (k+1)^\overline{r} \right]\]

ดังนั้น การอุปนัยชั้นแรกบน $r$ ก็คือ

\[P(r):\quad \forall k \left[ r! \;\Big\vert\; (k+1)^\overline{r} \right]\]

ซึ่งเราย่อมเห็นได้ทันทีว่า $P(0)$ จริงแน่นอน ด้วยสมมติฐานของการอุปนัย เราจะสมมติให้ $P(r)$ จริง เพื่อที่จะพิสูจน์ว่า $P(r+1)$ นั้นก็ต้องจริงด้วย

ถึงตอนนี้ เราจะทำการอุปนัยซ้อนลงไปอีกชั้นบน $k$ ดังนี้

\[P(r, k):\quad r! \;\Big\vert\; (k+1)^\overline{r}\]

เราก็จะเห็นอีกว่า $P(r+1, 0)$ นั้นจริง (เพราะด้านขวาของการหารลงตัวก็คือนิยามของแฟคทอเรียลเลย) ทำให้เราตั้งสมมติฐานว่า $P(r+1, k)$ จริงเพื่อพิสูจน์ $P(r+1, k+1)$ ต่อไป

ความเจ๋งของการอุปนัยสองชั้นนี้ก็คือ ตอนที่เราตั้งสมมติฐานชั้นนอกว่า $P(r)$ จริงนั้น เราจะได้ว่าสมมติฐานชั้นใน $P(r,\ell)$ ก็จะเป็นจริงไปหมดสำหรับทุกค่า $\ell$ ทันทีเลย (ทั้งที่เรายังพิสูจน์ชั้นในไม่เสร็จ!)² เราจะใช้งานสมมติฐานชั้นนอก $P(r)$ ที่เลือกค่าชั้นในเป็น $\ell=k+1$ ดังนั้น

\[r! \;\Big\vert\; (k+2)^\overline{r}\]

เพื่อความสะดวก ให้ $s\in\mathbb{N}$ เป็นผลหารจากการหารลงตัวดังกล่าว นั่นคือ $sr! = (k+2)^\overline{r}$

ถึงตรงนี้เราจะย้อนกลับมาดูสมมติฐานชั้นใน $P(r+1,k)$ ที่บอกว่า

\[\begin{align} (r+1)! &\;\Big\vert\; (k+1)^\overline{r+1} \\ &\;\Big\vert\; (k+1)(k+2)^\overline{r} \\ &\;\Big\vert\; (k+1)sr! \tag{1} \label{eq:inductive-step} \end{align}\]

เนื่องจากจำนวนนับใดๆ หารพหุคูณของตัวมันเองลงตัว เลือกพหุคูณเป็น $s$ บนตัวหาร $(r+1)!$ หรือก็คือ

\[(r+1)! \;\Big\vert\; s(r+1)! \iff (r+1)! \;\Big\vert\; (r+1)sr!\]

เพราะ $(r+1)!$ หาร $(k+1)sr!$ และ $(r+1)sr!$ ลงตัวทั้งคู่ ดังนั้นเราไล่ $\eqref{eq:inductive-step}$ ต่อได้ว่า

\[\begin{align} (r+1)! &\;\Big\vert\; (k+1)sr! + (r+1)sr! \\ &\;\Big\vert\; (k+1+r+1)sr! \\ &\;\Big\vert\; (k+2+r)(k+2)^\overline{r} \\ &\;\Big\vert\; (k+2)^\overline{r+1} \end{align}\]

ทำให้เราสรุปได้ว่า $P(r+1, k+1)$ จะเป็นจริงด้วยนั่นเอง ซ.ต.พ.

---

คิดบทพิสูจน์ซะซับซ้อนยืดยาว เพื่อที่จะไปเห็นว่าคนอื่นใช้อัตลักษณ์

\[\binom{n}{r} = \binom{n-1}{r-1} + \binom{n-1}{r}\]

มาพิสูจน์แบบอุปนัยธรรมดาๆ ก็ออกแล้ว 😂

Revision notes:

• March 11, 2024:

  ปรับปรุงคำอธิบายเพื่อให้เข้าใจได้ง่ายขึ้น(?)