ช่วงนี้เบื่อๆ เลยหาจังหวะเขียนโค้ดเล่น ก็บังเอิญกับที่ @taneekpet ส่งข่าวมาบอกว่า KBTG กำลังจัดแข่ง TechJam พอดี เลยมองซ้ายมองขวาคว้ามือ @ipats มาสมัครแข่งขันอย่างไม่คาดหวังอะไร 555 (ขนาดชื่อทีมยังตั้งว่า Monte Carlo เพราะกะว่าข้อไหนคิดไม่ออกก็จะสุ่มคำตอบเอาเลยละกัน)

เห็นว่าโจทย์มีความท้าทายดี (ขอชมทีมออกโจทย์มา ณ ที่นี้ด้วย) เลยมานั่งจดวิธีคิดและคำตอบไว้ซักหน่อย แต่เฉลยได้ไม่ครบทุกข้อนะเพราะจำ+ทำได้ไม่หมด … พร้อมหมายเหตุตัวโตๆ ว่าโค้ดที่แปะนี่คือทำความสะอาดมาเรียบร้อยแล้ว ตอนแข่งจริงโค้ดไม่ได้สวยงามขนาดนี้ 😅

รอบคัดเลือกทำผ่านอินเตอร์เน็ตให้เวลา 6 ชั่วโมง ตอนแรกเห็นว่าให้เวลามาซะเยอะเลย นึกว่าจะขำๆ เริ่มทำสี่ทุ่มเลิกทำเที่ยงคืน แต่สุดท้ายก็นั่งกดกันยันพระอาทิตย์ขึ้น (แข่งจบอารมณ์ไม่จบ ไล่หาคำตอบที่ถูกต้องไปอีก ถถถ)

ข้อเล็กๆ ถามสั้นตอบไว

ในกติกาให้คำแนะนำมาว่า ข้อเล็กๆ พวกนี้ควรเห็นโจทย์ปุ๊ปก็ตอบได้เลย ไม่ควรใช้เวลาเกินหนึ่งนาที ก็สงสัยว่าจะร้างราจากการแก้โจทย์แนวนี้มานาน ซัดไปข้อละห้าถึงสิบนาทีได้มั้ง … เอาจริงๆ จะให้ตอบหลักวินาทีเลยก็คงได้ แต่ความมั่นใจว่าจะถูกนี่ลดลงเหลือแค่ $1-\delta$ นะ 😝

สุ่มจากเหรียญลำเอียงให้ไม่ลำเอียง

โจทย์ให้เหรียญมาเหรียญหนึ่งซึ่งลำเอียงไปออกก้อย 51% และอยากได้วิธีที่จะเลียนแบบเหรียญที่ไม่ลำเอียง จึงขอให้เรียงความน่าจะเป็นที่วิธีทั้ง 4 นี้จะให้คำตอบลำเอียงน้อยสุดไปหามากสุด

1. โยนเหรียญไปร้อยครั้ง ถ้านับว่าออกหัวน้อยกว่า 49 ครั้งก็ตอบหัว มากกว่า 49 ครั้งก็ตอบก้อย
2. โยนเหรียญไปเรื่อยๆ จนกว่าจะออกก้อย หลังจากนั้นโยนเหรียญอีกหนึ่งครั้งแล้วตอบตามหน้าที่ออก
3. โยนเหรียญสองครั้ง ถ้าออกหัวทั้งคู่ก็ตอบหัว ออกก้อยทั้งคู่ก็ตอบก้อย
4. โยนเหรียญสองครั้ง ถ้าออกหัวแล้วก้อยให้ตอบหัว ถ้าออกก้อยแล้วหัวให้ตอบก้อย

ทั้งสี่วิธีข้างต้น ถ้าทำตามแล้วยังหาคำตอบไม่ได้ ก็ให้วนทำซ้ำไปเรื่อยๆ จนกว่าจะพบคำตอบ

ซึ่งถ้ามาวิเคราะห์ดู จะพบว่า

1. คิดจากผลรวมของการแจกแจงทวินาม $\Pr[X=r] = \binom{100}{r}(0.49)^r(0.51)^{100-r}$ โดยโอกาสออกหัวคือ $\Pr[0 \le X \le 48] \approx 0.4605 $ และโอกาสออกก้อยคือ $\Pr[50 \le X \le 100] \approx 0.4599$ พอเอามาคิดเป็นอัตราส่วนแล้วได้ประมาณ 50.03 ต่อ 49.97
2. การสุ่มแต่ละครั้งเป็นอิสระต่อกัน แม้จะสุ่มมาเรื่อยๆ จนออกก้อยแล้ว ก็ไม่ได้รับประกันว่าครั้งต่อไปจะออกหัวเพิ่มขึ้นแต่อย่างใด ดังนั้นอัตราส่วนจึงเป็น 49 ต่อ 51 เท่าเดิม
3. หัวทั้งคู่แล้วตอบหัวคือ $(0.49)^2 \approx 0.24$ ก้อยทั้งคู่แล้วตอบก้อยคือ $(0.51)^2 \approx 0.26$ ดังนั้นอัตราส่วนจะกลายเป็นประมาณ 48 ต่อ 52
4. เนื่องจากโอกาสออกหัวแล้วก้อยกับก้อยแล้วหัวมีค่าเท่ากัน และโอกาสที่หัวจะไปออกครั้งแรกหรือครั้งหลังก็เท่ากัน ดังนั้นวิธีนี้จึงแฟร์ที่สุด ให้อัตราส่วนเป็น 50 ต่อ 50 พอดีเป๊ะเลย

ดังนั้นข้อนี้ตอบ 4, 1, 2, 3

สร้างรูปจากสี่เหลี่ยม

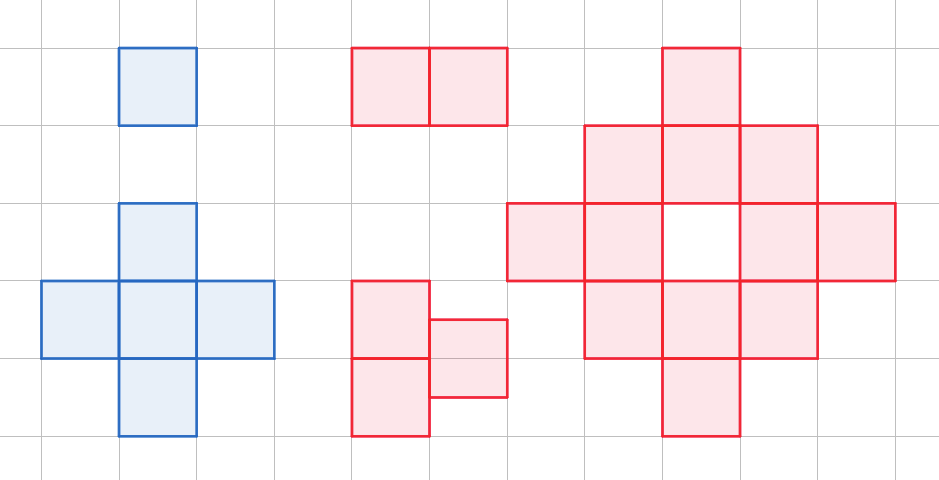
โจทย์ต้องการสร้างรูปทรงใหม่จากสี่เหลี่ยมจัตุรัสหนึ่งหน่วย โดยมีกฎว่า การสร้างรูปทรงใหม่ต้องนำสี่เหลี่ยมจัตุรัสวางบนกริดเท่านั้น ขอบของสี่เหลี่ยมจัตุรัสต้องเชื่อมกันทั้งหมด รูปทรงใหม่ที่ได้ต้องไม่มีรูตรงกลาง และที่ขอบของรูปทรงใหม่ทุกขอบต้องไม่มีขอบใดยาวเกินกว่าหนึ่งหน่วย ถามว่ารูปทรงใหม่ที่ใหญ่ที่สุดที่ไม่สามารถสร้างได้มีขนาดกี่หน่วย?

ตัวอย่างการสร้างรูปที่ถูกกฏ (สีน้ำเงิน) และผิด (สีแดง)

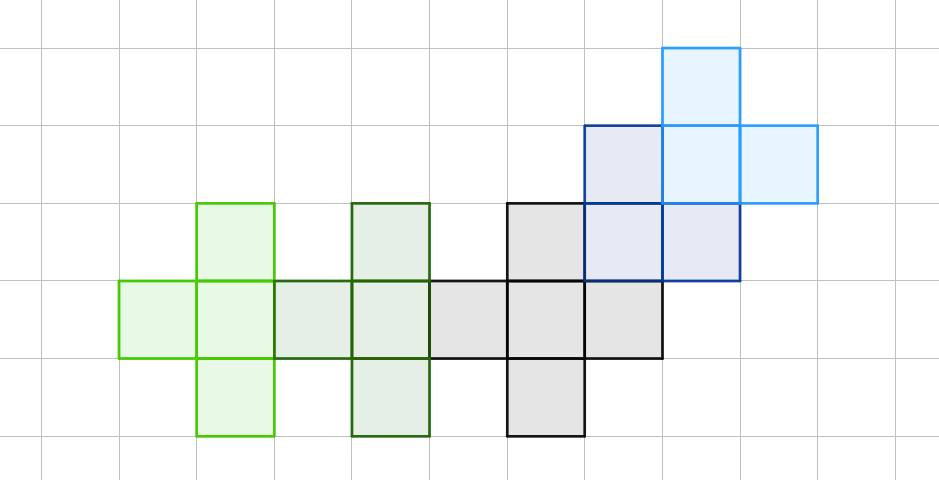
ข้อนี้ @ipats สังเกตอย่างรวดเร็วได้ว่า วิธีการที่จะเติมรูปสี่เหลี่ยมจัตุรัสลงไปเพื่อสร้างรูปทรงใหม่ สามารถตัดทอนรายละเอียดลงมาได้เหลือเพียง 2 วิธีเท่านั้น คือ

การต่อเติมรูปโดยไม่ขัดกฏ วิธีสีเขียวทางซ้ายจะเพิ่มครั้งละ 4 ส่วนวิธีสีน้ำเงินทางขวาเพิ่มครั้งละ 3

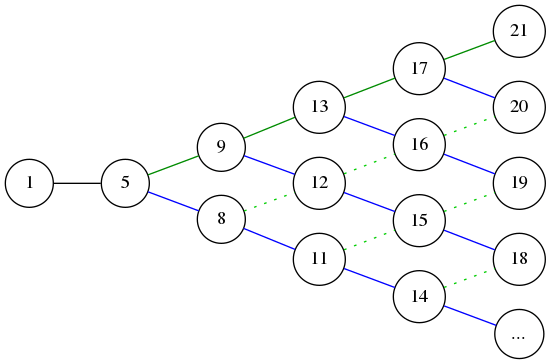
จึงได้สูตรของพื้นที่ที่เป็นไปว่า $5+4s_G+3s_B$ เมื่อ $s_G, s_B$ เป็นจำนวนครั้งที่ทำวิธีสีเขียวและน้ำเงินตามลำดับ หรือวาดออกมาเป็นแผนภาพได้ว่า

แผนภาพความเป็นไปได้ของพื้นที่ที่สร้างได้

จะเห็นว่า ไม่ว่าจะเลือกสลับใช้วิธีรวมกันแบบใด ถ้าทำไปอย่างน้อย 3 ครั้งจะสามารถสร้างพื้นที่ที่แตกต่างกันได้อย่างน้อย 4 แบบ แต่การเพิ่มพื้นที่หนึ่งครั้งให้พื้นที่เพิ่มมากที่สุดเพียง 4 หน่วย ดังนั้นหากเพิ่มพื้นที่มากกว่า 3 ครั้งจะสร้างพื้นที่หลังจากนั้นได้ครบทุกรูปแบบ

เราจึงเหลือแค่กรณีแรกๆ ให้พิจารณา ซึ่งไล่ดูด้วยตาก็ตอบได้ว่า พื้นที่ที่ใหญ่สุดที่สร้างไม่ได้คือ 10 หน่วย

เรียงเรียงเรียง

ข้อนี้ถามว่าถ้ารันอัลกอริทึมเรียงของในอาเรย์หลายๆ ครั้ง โดยแต่ละครั้งเรียงแค่บางส่วนของอาเรย์ การเรียงแบบไหนที่ให้ผลลัพธ์ที่อาเรย์ทั้งอาเรย์ยังเรียงลำดับไม่ถูกต้อง?

วิธีคิดข้อนี้อย่างง่ายที่สุด คงต้องเริ่มจินตนาการว่าสิ่งของในอาเรย์ถูกเรียงแบบกลับข้างกันไว้ก่อนแล้ว หลังจากนั้นจึงค่อยๆ ไล่ดูว่าการเรียงของทีละส่วนในอาเรย์ดังกล่าว รับประกันความถูกต้องของสิ่งของที่อยู่ตำแหน่งใดได้บ้าง

สมมติว่าอาเรย์ยาว 8 ตัวแล้วเราเลือกเรียง 6 ตัวแรก ตามด้วยเรียง 6 ตัวหลัง แล้วกลับไปเรียง 6 ตัวแรกอีกที จะได้ผลลัพธ์หลังการเรียงแต่ละครั้ง ดังนี้

0: 7 6 5 4 3 2 1 0
1: 2 3 4 5 6 7 1 0
2: 2 3 0 1 4 5 6 7
3: 0 1 2 3 4 5 6 7

นั่นก็คือ แม้การเรียงครั้งแรกจะไม่รับประกันเลยว่ามีสมาชิกตัวไหนในอาเรย์ที่อยู่ถูกตำแหน่ง แต่ถ้าดูส่วนที่ซ้อนทับกันระหว่างการเรียงครั้งแรกกับครั้งที่สองแล้ว จะพบว่าสมาชิก 4 ตัวตรงกลางก่อนการเรียงครั้งที่สองจะไปอยู่ตำแหน่งที่ถูกต้องแน่นอนหลังการเรียงครั้งที่สอง และเมื่อเรียงครั้งที่สามก็จะได้อาเรย์ที่เรียงลำดับเรียบร้อยทั้งอาเรย์พอดี

ไล่แบบนี้ก็น่าจะเจอคำตอบได้ไม่ยาก … ติดที่จำชอยส์เป๊ะๆ ไม่ได้ แต่มั่นใจว่าตอบถูกนะ (ตอนแข่งคิดวิธีวิเคราะห์ไม่ทัน เลยเขียนโปรแกรมมาสุ่มเรียงซะเลย 555)

นับกิ่งก้านใบ

โจทย์ให้โครงสร้างข้อมูลต้นไม้ทวิภาคที่สมบูรณ์มา ซึ่งหมายความว่าสำหรับโหนดใดๆ ถ้าโหนดนั้นไม่ใช่ใบ (มีลูกเท่ากับ 0) ก็ต้องเป็นกิ่งที่มีลูกทั้งซ้ายและขวาเท่านั้น (มีลูกเท่ากับ 2) ถามว่าจะนับจำนวนโหนดทั้งหมดในต้นไม้ด้วยฟังก์ชันนิรนามได้อย่างไร?

from collections import namedtuple

Node = namedtuple('Node', 'value left right')
Node.__new__.__defaults__ = (None, None, None)

def compute(tree, f, g):
    if tree.left is None and tree.right is None:
        return f(tree)
    else:
        return g(compute(tree.left, f, g), compute(tree.right, f, g), tree.value)

กระพริบตาก็รู้แล้วว่าข้อนี้แค่ส่งฟังก์ชันที่นับ 1 เมื่อเจอใบ และนับเพิ่มอีก 1 บวกกับผลลัพธ์จากการลงไปทำปัญหาย่อยทั้งซ้ายและขวาก็จะได้คำตอบแล้ว เช่นนี้

compute(tree, lambda _: 1, lambda lt, rt, _: lt + rt + 1)

แต่เนื่องจากเป็นโจทย์ชอยส์ (ที่จะบอกว่ากวนตีนก็ได้ 555) เลยไม่มีคำตอบนี้ให้เลือก! ติดสตันท์กันไปแป๊ปนึง @ipats ก็เตือนความจำว่า ต้นไม้มันเป็นแบบสมบูรณ์ ดังนั้นแม้จะรู้แค่จำนวนใบ ก็สามารถย้อนกลับไปคำนวณโหนดได้ ซึ่งมีสูตรคือ $\abs{V} = 2\abs{T} - 1$ เมื่อ $V, T$ คือโหนดและใบของต้นไม้ตามลำดับ

สูตรดังกล่าวสามารถพิสูจน์ได้ง่ายๆ ผ่านการอุปนัย โดยเริ่มจากต้นไม้ที่มีเพียง 1 โหนด จะเห็นว่าโหนดนี้ต้องเป็นใบด้วย หลังจากนั้นเมื่อต้องการเพิ่มขนาดต้นไม้ จะทำได้วิธีเดียวคือเปลี่ยนใบใดๆ ไปเป็นกิ่งที่แตกใบออกมา 2 ใบ ซึ่งกระบวนการนี้จะเพิ่มโหนดทั้งหมด 2 โหนด โดยหนึ่งในนั้นเป็นใบนั่นเอง ซ.ต.พ.

ดังนั้นข้อนี้จึงตอบ

compute(tree, lambda _: 1, lambda lt, rt, _: lt + rt) * 2 - 1

เลขสวยงาม

เลขสวยงามคือเลขที่เมื่อเขียนด้วยสตริงในฐาน 10 และแบ่งพาร์ทิชันแล้ว มีบางพาร์ทิชันที่ทุกซับสตริงเป็นจำนวนเฉพาะที่ไม่ขึ้นต้นด้วยเลขศูนย์ เช่น

• 863 เป็นเลขสวยงาม เพราะ 863 เป็นจำนวนเฉพาะ
• 357 เป็นเลขสวยงาม แม้ว่า 357 จะไม่เป็นจำนวนเฉพาะ แต่เราสามารถแบ่งพาร์ทิชัน 3|5|7 ที่ทำให้ทุกๆ ซับสตริงเป็นจำนวนเฉพาะได้
• 202 ไม่เป็นเลขสวยงาม แม้ 2 จะเป็นจำนวนเฉพาะ แต่การแบ่งพาร์ทิชัน 2|02 นั้นผิดกฎที่ห้ามมีเลขศูนย์นำหน้า (และการแบ่งพาร์ทิชันแบบอื่นๆ เช่น 20|2 ก็มีบางเลขที่ไม่ใช่จำนวนเฉพาะ)

คำถามคือ สำหรับตัวเลขทุกตัวที่เขียนได้ด้วยสตริงขนาด 5 ตัวอักษร มีเลขสวยงามทั้งหมดเท่าไหร่?

จำได้ว่าเคยเขียนอะไรแบบนี้ใน Project Euler มาแล้ว (หรืออาจจะไม่เคย แต่โจทย์คุ้นมาก) ก็เลยได้โค้ดนี้ออกมาอย่างรวดเร็ว

from collections import deque
from mathapi import prime       # github.com/neizod/mathapi

def partition(s):
    if s.startswith('0'):
        return
    if not s:
        yield deque()
    for i in range(1, len(s)+1):
        head = deque([s[:i]])
        for rest in partition(s[i:]):
            yield head + rest

def is_beautiful(n):
    for par in partition(str(n)):
        if all(int(s) in prime for s in par):
            return True
    return False

print(sum(is_beautiful(n) for n in range(10000, 100000)))

รันไป 5 วินาทีก็ได้คำตอบว่ามีเลขสวยงามอยู่ทั้งหมด 24,920 ตัว

ข้อใหญ่ๆ แก้โจทย์สนใจ Big-O

ทำข้อเล็กๆ เสร็จตั้งแต่ชั่วโมงครึ่งเห็นจะได้ ก็มาลุยกับข้อใหญ่ที่กติกาแนะนำว่าไม่ควรใช้เวลาเกินสามสิบนาทีต่อข้อ แถมทำเสร็จต้องมาเขียนอธิบายทั้งวิธีคิด, หาเทสเคสเพิ่มเติม, เล่าการทำงานของโปรแกรม, วิเคราะห์ความซับซ้อนด้านเวลาและพื้นที่อีก เลยเหลือพลังทำกันได้แค่ 2 ใน 3 ข้อเท่านั้น

ช่วยกันเก็บแอปเปิล

โจทย์ให้สวนแอปเปิล $A$ ที่มีแผนผังเป็นอาเรย์หนึ่งมิติมา โดยมีคนงาน 2 คนคือ Alice และ Bob ที่เก็บแอปเปิลจากต้นไม้ที่ติดกันได้ $K$ และ $L$ ต้นตามลำดับ ถ้าไม่ให้ Alice และ Bob เก็บแอปเปิลจากต้นซ้ำกัน ทั้งคู่จะเก็บแอปเปิลได้รวมกันมากที่สุดเท่าไหร่?

ข้อนี้ @ipats ตอบมาด้วยความรวดเร็วว่าแค่ sliding window ไปก็เสร็จแล้ว แต่คิดเทสเคสไปมาแล้วเจอบั๊ก เลยข้ามไปทำข้ออื่นก่อน (เพิ่งรู้ว่ามันข้ามไปทำข้ออื่นได้) แล้วกลับมาดีบั๊กต่อจนเสร็จครับ

โดยวิธีคิดเริ่มจากให้ Alice เป็นคนเริ่มเลือกเก็บแอปเปิลจากต้นไม้ $K$ ต้นติดกันเป็นคนแรก หาก Alice โลภ (greedy) และเลือกเก็บจาก $K$ ต้นที่ให้แอปเปิลสูงสุด อาจส่งผลเสียให้ Bob เหลือแอปเปิลบนต้นไม้ที่ติดกัน $L$ ต้นให้เก็บน้อยก็ได้ (ตัวอย่าง: $K=L=2$ และ $A=[1,2,23,42,3,1]$)

เราไม่มีทางรู้ (อย่างเร็วๆ) ได้เลยว่า Alice ต้องเลือกเก็บแอปเปิลจากต้นไม้ช่วงใด ถึงจะทำให้ Bob เก็บแอปเปิลมารวมกันแล้วได้ผลลัพธ์ที่ดีที่สุด ดังนั้นเราจึงให้ Alice ทดเก็บวิธีที่เก็บแอปเปิลทุกวิธีไปเลย

ซึ่งเราจะมองว่า หลังจาก Alice เลือกช่วงต้นไม้ที่จะเก็บแอปเปิลไปแล้ว สวนจะถูกแบ่งออกเป็น 2 ฝาก ซึ่ง Bob จะเข้าไปเก็บแอปเปิลในสวนใดสวนหนึ่งที่ให้ผลลัพธ์สูงสุด หากเราสามารถหาว่า Bob ต้องเก็บแอปเปิลที่ต้นไหน เราก็จะสามารถแก้โจทย์ข้อนี้ได้

การจะทำเช่นนั้นได้ เราเริ่มให้ Bob ทดไว้ว่าถ้าเลือกแอปเปิลจากต้นที่ $1$ ถึง $L$ จะได้แอปเปิลได้จำนวนเท่าไหร่ และ Alice ทดไว้ว่าถ้าเลือกเก็บแอปเปิลจากต้น $L+1$ ถึง $L+K$ ได้เท่าไหร่ … ตรงนี้เราจะเห็นว่า Bob เลือกเก็บแอปเปิลที่เป็นไปได้มากที่สุดแล้วในสวนฝั่งซ้ายมือ ดังนั้นผลรวมแอปเปิลที่มากที่สุด เมื่อ Alice เลือกเก็บที่ตำแหน่งนี้คือ การเลือกเก็บตั้งแต่ต้น $1$ ถึง $L+K$

  maxL
|------|
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 ...
|------| |---------|
    L         K

ในรอบถัดมา ให้ Alice เลื่อนไปเริ่มเก็บแอปเปิลที่ต้นถัดไป (ต้นที่ $L+2$ ถึง $L+K+1$) และให้ Bob เลื่อนไปเริ่มเก็บที่ต้นถัดไป (ต้นที่ $2$ ถึง $L+1$) เช่นกัน คราวนี้เราจะเปรียบเทียบว่า Bob เก็บของใหม่ได้ดีกว่าของเดิมหรือไม่ หากเก็บได้มากกว่าก็จะอัพเดทค่าสูงสุดของ Bob ที่เก็บได้ในสวนฝั่งซ้ายมือ แล้วหาค่าผลรวมแอปเปิลจากตำแหน่งปัจจุบันที่ Alice เลือกเก็บและจากค่าสูงสุดของ Bob

     maxL
   |------|
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 ...
   |------| |---------|
       L         K

เราค่อยๆ ขยับตำแหน่งของ Alice และ Bob ไปเรื่อยๆ และคอยจำว่าตำแหน่งใหม่ของ Bob เก็บแอปเปิลได้มากกว่าเดิมหรือไม่ ดังนั้นเราจะได้ผลรวมแอปเปิลสูงสุดที่ Alice กับ Bob สามาถเก็บได้นั่นเอง

        maxL
      |------|
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 ...
            |------| |-----------|
                L          K

อย่างไรก็ตาม การเก็บแอปเปิลตามวิธีข้างต้นนั้น เราสนใจแต่การให้ Bob เก็บแอปเปิลให้ได้มากที่สุดในสวนฝั่งซ้ายอย่างเดียว เพื่อให้ผลลัพธ์ที่สมบูรณ์ เราต้องวิ่งจากด้านขวาของสวนกลับมาด้านซ้ายด้วย หรือก็คือทำกระบวนการข้างต้นอีกครั้งโดยกลับอาเรย์ $A$ นั่นเอง

เพราะเราวิ่งผ่านอาเรย์แค่ 2 รอบ เวลาที่ใช้จึงเป็น $O(n)$

def aux(A, K, L):
    ck = sum(A[L:K+L])
    cl = sum(A[:L])
    ml = max(0, cl)
    ans = cl + ck
    for i in range(K+L, len(A)):
        ck += A[i] - A[i-K]
        cl += A[i-K] - A[i-K-L]
        ml = max(ml, cl)
        ans = max(ans, ck + ml)
    return ans

def solution(A, K, L):
    if K + L > len(A):
        return -1
    return max(aux(A, K, L), aux(A[::-1], K, L))

อินเดียน่า โจนส์ กับเลเซอร์ตุ๊กตากระจก

โจทย์มองแผนที่ห้องจากมุมมองนกลงมาเป็นพิกัดคาร์ทีเซียน โดยให้อินเดียน่า โจนส์ยืนอยู่กลางห้องที่ตำแหน่ง $(0,0)$ และมีเซตของตุ๊กตากระจก $A$ ที่แต่ละตัวอยู่ที่ตำแหน่ง $(x_i,y_i)$ ต่างๆ ถามว่าโจนส์ต้องยิงเลเซอร์ออกไปกี่เส้น ถึงจะโดนตุ๊กตากระจกทุกตัวในห้องนั้น (โดยยิงทะลุตุ๊กตาตัวหน้าไปยังตัวหลังได้)

ข้อนี้ง่ายมาก ใช้แค่ความรู้คณิตศาสตร์พื้นฐานเท่านั้น และถ้ารู้จักโครงสร้างข้อมูลที่เหมาะสมก็ไม่ต้องพึ่งอัลกอริทึมยากๆ เลย

เนื่องจากเรายืนอยู่ที่จุด $(0,0)$ และมองเห็นตุ๊กตาตัวที่ $i$ ที่ตำแหน่ง $(x_i,y_i)$ ถ้าตุ๊กตาตัวที่ $i$ และ $j$ อยู่ในเส้นสายตาเดียวกัน (โดยไม่เสียนัยทั่วไป หมายถึงเราสามารถยิงเลเซอร์ไปยัง $(x_i,y_i)$ และทะลุไปหา $(x_j,y_j)$ ได้) นั่นหมายความว่าตุ๊กตาตัวที่ $i$ และ $j$ อยู่บนเส้นความชันเดียวกัน หรือก็คือสามารถหาค่า $s$ และ $t$ บางค่าที่ทำให้สมการนี้เป็นจริง

ซึ่งมีคำตอบคือ $s = 1/\gcd(x_i,y_i)$ และ $t = 1/\gcd(x_j,y_j)$

สำหรับฟังก์ชัน $\gcd$ เป็นฟังก์ชันที่คำนวณหาค่าห.ร.ม.ของตัวเลขจำนวนเต็มสองตัว เมื่อนำไปหาค่า $s,t$ ตามข้างต้น จะทำให้พิกัดของตุ๊กตาที่ได้มีค่าเป็นเศษส่วนอย่างต่ำเสมอ หรือก็คือ ตุ๊กตาสองตัวที่อยู่ในแนวเส้นสายตาเดียวกัน เมื่อหารด้วยห.ร.ม.แล้ว จะมีพิกัดเดียวกัน

เราสามารถนับเฉพาะตุ๊กตาที่แปลงพิกัดเป็นเศษส่วนขั้นต่ำแล้วเพื่อบอกว่าต้องยิงเลเซอร์กี่ลำแสงได้เลย

แต่เพราะ $\gcd$ สามารถคืนค่าได้ทั้งบวกและลบ ทำให้การแปลงเศษส่วนขั้นต่ำด้วยการหารค่า $\gcd$ ตรงๆ ของ $(x_i,y_i)$ และ $(-x_i,-y_i)$ คืนค่าเป็นพิกัดเดียวกัน แต่โจทย์ข้อนี้บังคับให้ใช้เลเซอร์สองเส้นเพื่อยิงในทิศทางตรงข้ามกัน ดังนั้นจึงต้องเปลี่ยนไปหารด้วยค่าสัมบูรณ์ของ $\gcd$ แทน เพื่อไม่ให้เสียข้อมูลพิกัดควอแดรนท์ตั้งต้นของตุ๊กตาแต่ละตัว

เนื่องจากการหา $\gcd(x,y)$ แต่ละครั้งกินเวลา $O(\log xy)$ เวลารวมทั้งหมดจึงเป็น $O(n \log xy)$

from fractions import gcd

def irreducible(point):
    denom = abs(gcd(point.x, point.y))
    return (point.x//denom, point.y//denom)

def solution(A):
    return len({irreducible(point) for point in A})

ช่วงที่ขนาดใหญ่สุดที่ได้ผลรวมตามที่ต้องการ

โจทย์ให้อาเรย์ $A$ ที่มีแต่ตัวเลข $\lbrace-1, 0, 1\rbrace$ และผลรวม $S$ ที่ต้องการมา แล้วถามว่าซับอาเรย์ที่มีผลรวมเป็นค่าที่ต้องการมีขนาดใหญ่ที่สุดเป็นเท่าไหร่?

คิดในเวลาไม่ออก เลยเขียนแบบถึกส่งแบบ $O(n^2)$ ไป จนได้ฟังเฉลยจากการพูดคุยกับทีมอื่นๆ ที่ผ่านเข้ารอบชิงภาคกลาง ซึ่งแก้ปัญหาดังกล่าวด้วยกำหนดการพลวัต ด้วยแนวคิดดังนี้

สร้างตารางจดค่า prefix และ postfix ของผลรวมตั้งแต่ช่องแรกไปจนถึงตำแหน่งใดๆ ในอาเรย์ หลังจากนั้นดูว่าแต่ละค่า $C$ ที่สร้างได้ในตาราง postfix เมื่อนำไปลบกับค่า $S$ ที่ต้องการแล้วมีอยู่ในตาราง prefix หรือไม่ ถ้ามีก็แปลว่าเราสามารถสร้างผลรวม $S$ นั้นได้ โดยมีความยาวมากสุดจากตำแหน่งของ $C$ ใน postfix ลบกับตำแหน่งของ $C-S$ ใน prefix นั่นเอง

def make_prefix(A):
    count = 0
    table = {}
    for idx, val in enumerate(A):
        count += val
        if count not in table:
            table[count] = idx
    return table

def make_postfix(A):
    count = 0
    table = {}
    for idx, val in enumerate(A):
        count += val
        table[count] = idx
    return table

def solution(A, S):
    prefix = make_prefix(A)
    postfix = make_postfix(A)
    print(max({postfix[C]-prefix[C-S] for C in postfix if C-S in prefix}))

เปลี่ยนอัลกอริทึมแล้วความเร็วเพิ่มเป็น $O(n)$ กราบๆๆ

สรุป

แน่นอนว่าลงแข่งแบบไม่ได้คาดหวังอะไร แต่สุดท้ายก็ดันเข้ารอบซะงั้น (ส่วนคนส่งข่าวดันไม่เข้ารอบตาม – อดเจอเลย) … ก็ต้องไปลุ้นเอาว่าวันแข่งจริงจะเจอคนรู้จักให้เข้าไปทักทายบ้างมั้ย แต่ได้หาเพื่อนใหม่ก็คงจะสนุกไปอีกแบบ 😅

Originally published on: neizod's (แตกตัวจากความยาว)

neizod

author