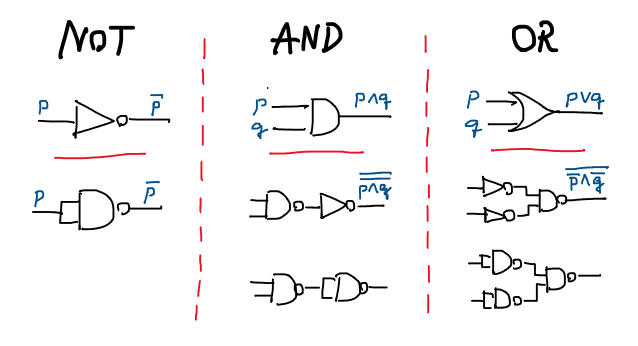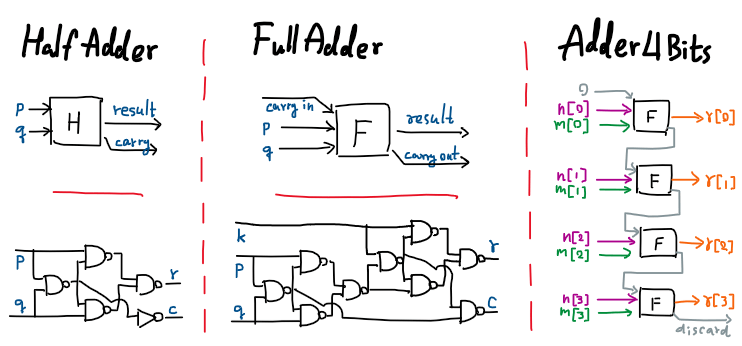
คอมพิวเตอร์นั้นแท้จริงแล้วก็คือระบบตรรกะที่ซับซ้อนมากๆ ระบบหนึ่ง นั่นก็คือเราสามารถคำนวณสิ่งต่างๆ ได้ผ่านการนำตัวดำเนินการ $\wedge,\vee,\neg$ (AND/OR/NOT — เพื่อความสะดวก ในที่นี้จะเขียนนิเสธด้วยเส้นขีดยาวข้างบนแทน) มาทำงานร่วมกัน เช่น ถ้าเรามีจำนวนนับสองตัว $n,m$ ที่เขียนผ่านเลขฐานสองขนาด 4 บิต เราสามารถคำนวณ $n+m$ ได้จาก

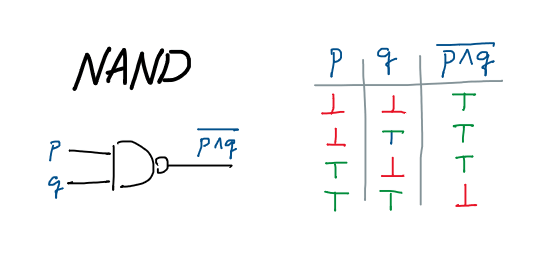
\[\begin{align} p {\;\!\Rightarrow\;\!} q &= p \vee \overline{q} \\ p \oplus q &= \overline{(p {\;\!\Rightarrow\;\!} q) \wedge (q {\;\!\Rightarrow\;\!} p)} \hspace{-2em} \\ H(p,q) &= (p \oplus q, p \wedge q) \\ F(k,p,q) &= (r, c_1 \vee c_2) & \text{where}\quad & (i,c_1) = H(p,q) \\ &&& (r,c_2) = H(i,k) \\ n[0..3] + m[0..3] &= r[0..3] & \text{where}\quad & (r[0],c_0) = F(\bot, n[0], m[0]) \\ &&& (r[1],c_1) = F(c_0, n[1], m[1]) \\ &&& (r[2],c_2) = F(c_1, n[2], m[2]) \\ &&& (r[3],c_3) = F(c_2, n[3], m[3]) \end{align}\]

การมีตัวดำเนินการพื้นฐาน AND/OR/NOT เพียแค่ 3 ตัวก็ทำให้เราสามารถทำงานทุกอย่างได้ครบถ้วนสมบูรณ์แล้ว แต่ว่าเรายังทำได้ดีกว่านี้ไปอีกโดยลดจำนวนตัวดำเนินการพื้นฐานให้เหลือเพียงแค่ตัวเดียว นั่นคือ ในระดับวงจรคอมพิวเตอร์ เราจะเริ่มจากการมีแค่วงจร NAND (Not AND) ที่ทำงานเช่นนี้

จะเห็นว่าเราสามารถสร้างตัวดำเนินการ NOT/AND/OR ได้จาก NAND ดังนี้

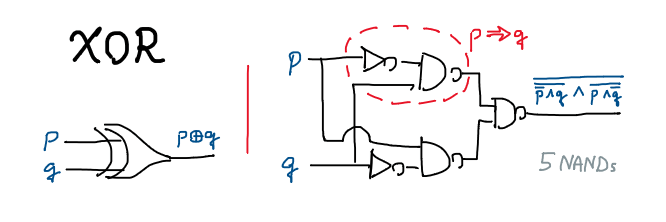
ประเด็นคือ ในคอมพิวเตอร์เรามักใช้งานตัวดำเนินการอีกตัวนึงบ่อยมากๆ นั่นก็คือ XOR (eXclusive OR, สัญลักษณ์ $\oplus$) ซึ่งแน่นอนว่าในระดับแนวคิดแล้ว เราสามารถสร้างมันได้ง่ายๆ ตามนิยามข้างต้นเลยว่า

ปัญหาคือการแปลงสมการคณิตศาสตร์มาเป็นวงจรแบบตรงไปตรงมาเช่นนี้ มันจะใช้ NAND ถึง 5 ตัวในการทำงาน ซึ่งไม่ดีแน่สำหรับตัวดำเนินการที่ถูกเรียกใช้งานบ่อยๆ ดังนั้นคำถามคือเราจะลดขนาดมันให้ใช้ NAND น้อยลงกว่านี้ได้หรือไม่/ได้อย่างไร

ถ้าเรากลับไปพิจารณาสมการของ XOR ตั้งแต่ต้นอีกครั้ง จะได้ว่า

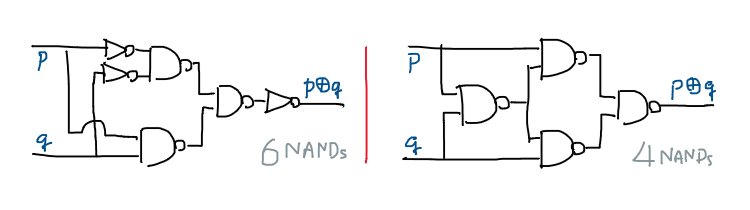
\[\begin{align} p \oplus q &= \overline{(p {\;\!\Rightarrow\;\!} q) \wedge (q {\;\!\Rightarrow\;\!} p)} \\ &= \overline{(p \vee \overline{q}) \wedge (q \vee \overline{p})} \\ &= \overline{(p \wedge q) \vee \cancel{(p \wedge \overline{p})} \vee \cancel{(\overline{q} \wedge q)} \vee (\overline{q} \wedge \overline{p})} \\ &= \overline{(p \wedge q) \vee (\overline{q} \wedge \overline{p})} \end{align}\]

ขอพักครึ่งทางตรงนี้แป๊บนึง เพื่อให้เราได้สัมผัสถึงความงามของนิยามอีกแบบหนึ่งของ XOR ที่สำหรับมนุษย์แล้วอาจถือว่าเข้าใจได้ง่ายกว่านิยามแรก อย่างไรก็ตาม หากเราต่อวงจรตามสมการนี้ จะพบว่าเราใช้วงจร NAND มากขึ้นกลายเป็น 6 ตัว! ดังนั้นเราจะไล่สมการเพิ่มอีกหน่อยจนได้

\[\begin{align} p \oplus q &= \overline{(p \wedge q) {\color{blue}\:\vee\:} (\overline{q} {\color{red}\:\wedge\:} \overline{p})} \\ &= \overline{((p \wedge q) {\color{blue}\:\vee\:} \overline{q}) {\color{red}\:\wedge\:} ((p \wedge q) {\color{blue}\:\vee\:} \overline{p})} \\ &= \overline{\overline{\overline{p \wedge q} \wedge q} \wedge \overline{\overline{p \wedge q} \wedge p}} \end{align}\]

ดูเผินๆ เหมือนว่าเราจะกลับมาที่เดิมที่ใช้ NAND 5 ตัว แต่สังเกตว่า $\overline{p \wedge q}$ นั้นถูกใช้ซ้ำสองครั้ง ดังนั้นเมื่อแปลงเป็นวงจรจริงๆ เราจะใช้ NAND เหลือเพียงแค่ 4 ตัวเท่านั้น! (และใช้น้อยสุดเท่าที่เป็นไปได้แล้ว – ลองพิสูจน์โดยการแจกแจงแผงวงจรทั้งหมดที่ใช้ NAND น้อยกว่านี้ดูได้)

ความเจ๋งของท่านี้ก็คือ ตอนเอา XOR ไปสร้าง halfadder ต่อ เราจะได้ $\overline{p \wedge q}$ มาฟรีๆ ดังนั้นส่วนที่มันต้องคืนค่า carry (ซึ่งก็คือ $p \wedge q$) เราจึงต้องการวงจร NOT เพิ่มอีกแค่ตัวเดียวก็พอ ดังนั้น halfadder จึงสร้างจาก NAND ได้ใน 5 ตัว

ยิ่งไปกว่านั้น สำหรับ fulladder (ซึ่งสร้างจาก halfadder สองอัน) เราก็ยังประหยัด NAND ได้อีกรอบเพราะ carry out ตอนนี้สร้างได้จากการ OR carry ระหว่างทางสองอัน ซึ่งเมื่อกระจายมันออกมาแล้วตัด NOT ระหว่างทางทิ้งไป ก็จะเหลือแค่ NAND ที่จำเป็นเพียงแค่ตัวเดียว รวมเป็นว่า fulladder จะใช้ nand แค่ 9 ตัว

แล้วถ้าเราไม่อยากใช้วงจร NAND เพียงวงจรเดียวเป็นพื้นฐาน จะมีวงจรอื่นที่สามารถทำหน้าที่แบบนี้ได้อีกมั้ย? ก็มีอีกทางเลือกหนึ่งคือวงจร NOR ที่สามารถถูกนำไปสร้างเป็นวงจรอื่นๆ ทั้งหมดได้เช่นกัน เพียงแต่ว่าที่หนังสือเรียนมักหยิบวงจร NAND มาสอนเป็นหลัก หนึ่งในสาเหตุก็คงเพราะว่าการสร้าง XOR จาก NOR นั้นต้องใช้ NOR ขั้นต่ำถึง 5 ตัวหล่ะมั้ง…

อนึ่ง ชิปคอมพิวเตอร์ปัจจุบันนั้นไม่ได้สร้างทุกอย่างขึ้นมาจากวงจร NAND เพียงอย่างเดียวอีกต่อไปแล้ว แต่ออกแบบโดยใช้วงจรพื้นฐานอื่นๆ ที่ซับซ้อนแต่เหมาะสมตามสถานการณ์มาทำงานร่วมกันแทน เพื่อให้ในภาพรวมแล้วเราสามารถประหยัดพื้นที่/อัตรากินไฟของชิปทั้งอันได้นั่นเอง