บวกเลขโดยไม่ใช้เครื่องหมายบวก
เพื่อนในแลปเล่าให้ฟังว่า เจอโจทย์ฝึกสัมภาษณ์งานที่ให้เขียนโปรแกรมเพื่อบวกจำนวนเต็มสองตัวโดยห้ามใช้เครื่องหมายบวก(และลบ) … คือแว๊บแรกก็เข้าใจแหล่ะว่า โจทย์นี้ต้องการทดสอบพื้นฐานการจัดการข้อมูลในระดับบิต ซึ่งก็โอเค คำตอบก็แค่จับ nand gate มาประกอบเป็น halfadder, fulladder เพื่อทำงานบน 2’s compliment ก็เสร็จแล้ว (ถ้ายังจำเทคนิคเหล่านั้นได้จากสถาปัตยกรรมคอมพิวเตอร์อะนะ)
แต่ตัวโจทย์จริงๆ ไม่ได้บอกว่าให้ทำท่า logic gate แบบนั้นซักหน่อย เค้าแค่ถามว่าให้เขียนโปรแกรมบวกเลขโดยห้ามใช้เครื่องหมายบวก(และลบ)แค่นั้นเอง (ซึ่งก็นั่นแหละ โจทย์นี้มันเป็นโจทย์ที่ดีหรือเปล่า นั่นก็เป็นประเด็นที่น่าเก็บไปคิด) … งั้นถ้าเราจะกวนตีนโจทย์นี้กลับโดยการเขียนโปรแกรมแบบอื่นไปเลยที่บวกเลขได้เหมือนกัน เพียงแค่ไม่ใช้เครื่องหมายบวกมันจะทำได้มั้ย
โจทย์ไม่ได้ห้ามเครื่องหมายคูณ/หาร/มอดูโล เพราะงั้นเราอาจเขียนแบบนี้เอาก็ได้ 555555
add n 0 = n
add n m = add (m * succ (div n m)) (mod n m)
โค้ดข้างต้นนี้จริงๆ ก็แอบโกงไปหน่อย เพราะปรกติแล้วเราเริ่มจากนิยามการบวก/ลบเป็นพื้นฐานก่อน แล้วหลังจากนั้นค่อยมานิยามคูณ/หาร แม้ว่าโค้ดนี้จะคอมไพล์ผ่านนำไปใช้งานในโลกจริงได้ แต่มันก็ไม่ถูกต้องตามการให้เหตุผลทางคณิตศาสตร์ซักเท่าไหร่ (เพราะเป็นการนิยามวกวนนั่นเอง)
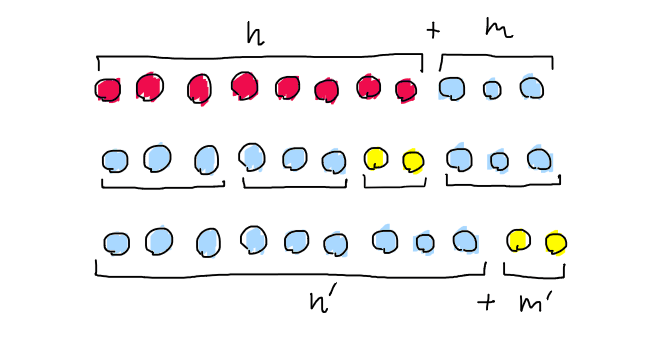
แล้วเราจะเขียนยังไงให้ถูกตามหลักคณิตศาสตร์? ก็คงต้องย้อนกลับไปตั้งแต่การนิยามจำนวนนับ ซึ่งตั้งอยู่บนรากฐานของสัจพจน์ Peano ที่เริ่มจากการมีเลขศูนย์เป็นตัวเลขตัวแรก แล้วใช้ฟังก์ชัน “สมาชิกตัวถัดไป” (successor) เพื่อสร้างตัวเลขที่เหลือ นั่นก็คือเราจะสร้างเลขหนึ่งโดยการบอกว่ามันเป็นสมาชิกตัวถัดมาจากศูนย์ สร้างเลขสองซึ่งเป็นสมาชิกตัวถัดมาจากหนึ่ง เช่นนี้ไปเรื่อยๆ
zero = 0
one = succ zero
two = succ one -- succ (succ zero)
three = succ two -- succ (succ (succ zero))
...
จึงทำให้เรานิยามการบวกได้ว่า
add n 0 = n
add n (succ m) = succ $ add n m
โอเค สำหรับ Haskell แล้วโค้ดนี้ไม่ถูกต้องเสียทีเดียว ถ้าจะคอมไพล์ให้ผ่านต้องใช้ pred เข้ามาช่วยอีกแรง นั่นคือเขียนบรรทัดที่สองเป็น add n m = succ $ add n $ pred m แทน เพราะว่า Haskell ไม่รองรับการจับคู่รูปแบบที่เขียนเป็นฟังก์ชันได้ … ถ้าจะเขียนให้ถูกก็ต้องย้อนกลับไปตั้งแต่นิยามระบบตัวเลขแบบนี้
data Peano = Zero | Succ Peano deriving (Show)
add n Zero = n
add n (Succ m) = Succ $ add n m
ความเจ๋งก็คือ ท่าข้างต้นนี้มันเรียบง่ายมากๆ จนเราสามารถขยายมันไปยังนิยามการคูณและยกกำลังในทำนองเดียวกันได้อย่างง่ายดาย นั่นก็คือ
mul n Zero = Zero
mul n (Succ m) = add n $ mul n m
pow n Zero = Succ Zero
pow n (Succ m) = mul n $ pow n m
เอาไปใช้จริงได้มั้ยนั่นอีกเรื่อง 😜
ป.ล. ไหนๆ ก็ไหนๆ ส่งท้ายด้วยคำตอบเวอร์ชัน logic gate ไว้ด้วยดีกว่า
nandG 1 1 = 0
nandG _ _ = 1
notG a = nandG a a
andG a b = notG (nandG a b)
orG a b = nandG (notG a) (notG b)
xorG a b = notG (orG (andG a b) (notG (orG a b)))
halfadder a b = (xorG a b, andG a b)
fulladder a b c = (f, orG c1 c2)
where (i,c1) = halfadder a b
(f,c2) = halfadder i c
add n m = aux n m 0
where aux 0 0 0 = 0
aux n m c = append r $ aux (shiftR n) (shiftR m) k
where (r,k) = fulladder (leastB n) (leastB m) c

author