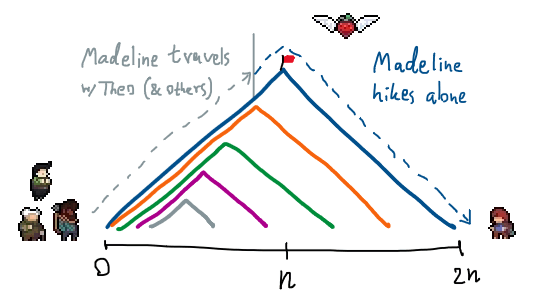
IOI 1992: ปีนเขากันเป็นทีม
โจทย์จากการแข่งขัน IOI 1992 เอาจริงโจทย์ข้อนี้ก็อาจเรียกได้ว่าไม่ใช่โจทย์ที่ยากหรือโดดเด่นเท่าไหร่ (เมื่อเทียบกับโจทย์อื่นๆ) แต่ส่วนตัวแล้วก็เรียกได้ว่ามีความทรงจำร่วมกับโจทย์นี้พอสมควร เพราะว่ามันเป็นโจทย์แรกๆ ที่เปิดโลกให้เรารู้จักการนำคอมพิวเตอร์มาช่วยแก้โจทย์ปัญหาเลยหล่ะ1
ปีนเขาให้เหนื่อยทำไม เดี๋ยวนี้เค้ามีรถกระเช้ากันแล้ว 😜
ทีนี้ถ้าเราไปหาโจทย์ต้นฉบับมาอ่านแล้วมองด้วยเลนส์ของการแข่งแก้โจทย์ในปัจจุบันก็จะรู้สึกว่าอิหยังวะมากๆ เพราะว่าเกณฑ์การให้คะแนนนั้นมีเรื่องของการ “พิมพ์ข้อความบนหน้าจอเพื่อบอกให้ป้อนข้อมูล (และปฏิเสธข้อมูลที่ไม่ตรงตามข้อจำกัด)” อย่างถูกต้องด้วย! (ปัจจุบันผู้เข้าแข่งขันไม่ต้องห่วงเรื่องการนำเข้าข้อมูล สามารถถือว่าข้อมูลนำเข้านั้นถูกต้องตรงตามข้อจำกัดได้เลย) นั่นก็คงเป็นเพราะว่าการแข่งในปีนั้นเป็นเพียงการแข่งปีที่ 4 ของโอลิมปิกวิชาการคอมพิวเตอร์ ซึ่งมันยังไม่มีระบบตรวจคำตอบแบบอัตโนมัติ หมายความว่าเมื่อเขียนโปรแกรมเสร็จก็จะต้องเรียกกรรมการมาตรวจคำตอบด้วยการนั่งพิมพ์ข้อมูลนำเข้าด้วยมือและดูคำตอบด้วยตานั่นเอง (เท่าที่เคยอ่านมานะ เกิดไม่ทันไปแข่งเอง รอผู้รู้มายืนยันอีกที)
แต่ถ้าเราจะพยายามแปลงโจทย์ข้อนี้มาให้อยู่ในกรอบของการแข่งเขียนโปรแกรมในปัจจุบัน (ซึ่งก็คงต้องทำอย่างนั้น เพราะว่าส่วนคำถาม-คำตอบมันไม่เหลือแล้ว) ก็คงจะเล่าได้ว่า มีนักปีนเขากลุ่มหนึ่งที่มีสามาชิก $p$ คน โดยทุกคนปีนเขาได้เร็วเท่ากัน (และเร็วเท่ากันในทั้งขาขึ้นและขาลง) อย่างไรก็ตาม นักปีนเขาแต่ละคนจะแบกสัมภาระและต้องการอาหารเป็นปริมาณไม่เท่ากัน นั่นคือนักปีนเขาคนที่ $i$ แบกข้าวติดตัวไปได้ $s_i$ กล่อง แต่ว่าก็ต้องการกินข้าววันละ $c_i$ กล่องด้วยเช่นกัน สมมติว่าภูเขาลูกหนึ่งใช้เวลา $n$ วันในการปีนไปจนถึงยอด ซึ่งภูเขาลูกนี้มันอาจจะสูงมากๆ จนนักปีนเขาแต่ละคนไม่สามารถปีนไปถึงยอดและกลับลงมาได้ด้วยตนเองได้ (โดยไม่อดตายไปซะก่อนระหว่างทาง) กลุ่มนักปีนเขาจึงรวมตัวกันเพื่อวางแผนการปีนเขาให้มีอย่างน้อยหนึ่งคนพิชิตยอดเขาได้ โดยมีแนวทางการปีนเขาดังนี้
- นักปีนเขาทุกคน (ที่ได้รับเลือกให้ออกเดินทาง) จะเริ่มออกเดินทางพร้อมกันทั้งหมด
- นักปีนเขาบางคนจะเป็นผู้เสียสละหันหลังกลับระหว่างทางพร้อมยกอาหารส่วนเกินให้นักปีนเขาคนอื่นๆ
- นักปีนเขาแต่ละคนไม่สามารถหยุดรอที่กลางทาง หรือออกเดินทางอีกครั้งทีหลังได้
ดังนั้นคำถามก็คือ มันจะมีวิธีจัดกลุ่มนักปีนเขาอย่างเหมาะสมเพื่อให้ทำภารกิจนี้ได้สำเร็จมั้ย? และถ้ามีแล้วตารางการปีนเขาของนักปีนแต่ละคนจะเป็นอย่างไร? โดยเราจะถือว่าปัญหานี้ถูกแก้ได้อย่างเหมาะสมที่สุดเมื่อเลือกใช้นักปีนเขาได้เป็นจำนวนน้อยที่สุด และในบรรดาวิธีที่ใช้นักปีนเขาเป็นจำนวนน้อยสุดนี้ก็ยังใช้อาหารน้อยสุดอีกด้วย (นั่นคือแม้จะสามารถลดการเตรียมเสบียงอาหารให้น้อยลงได้ แต่หากต้องแลกมากับการใช้นักปีนเขาเป็นจำนวนมากขึ้น ก็จะถือว่าไม่เหมาะสมในกรอบของโจทย์ข้อนี้) อนึ่ง ข้อจำกัดของโจทย์คือ $n\le100$ และ $p\le20$ และ $s,c \in \mathbb{Z}^+$
ตัวอย่างแรก
- จำนวนวันปีนเขาถึงยอด $n=2$
- นักปีนเขามีแค่คนเดียว ซึ่งสามารถแบกข้าวได้สามกล่อง และกินข้าววันละหนึ่งกล่อง
สังเกตว่าแม้เราจะใช้เวลาแค่สองวันในการปีนขึ้นไปจนถึงยอดเขา แต่ว่าเราก็ยังต้องปีนลงเขากลับมาที่ฐานด้วย ดังนั้นเวลารวมในการปีนเขาจริงๆ คือสี่วัน ซึ่งจะเห็นว่าไม่สามารถทำได้
ตัวอย่างที่สอง
- จำนวนวันปีนเขาถึงยอดคือ $n=4$
- กลุ่มนักปีนเขาสามารถแบกข้าว/ต้องการกินต่อวัน คือ $\lbrace (7,1),(8,2),(12,2),(15,3),(7,1) \rbrace$
คำตอบคือใช้นักปีนเขาสองคน ได้แก่คนแรกและคนสุดท้าย โดยแบกข้าวไปรวมกันเท่ากับสิบกล่อง ซึ่งคนที่จะเสียสละแบกข้าวกล่องให้เพื่อน จะต้องหันหลังกลับในวันที่หนึ่ง
ตัวอย่างที่สาม
- จำนวนวันปีนเขาถึงยอดคือ $n=10$
- กลุ่มนักปีนเขามีจำนวนไม่จำกัด โดยแต่ละคนกินข้าววันละหนึ่งกล่อง และแบกข้าวได้ $s=12$ กล่อง
คำตอบคือใช้นักปีนเขา 5 คน โดยให้หนึ่งคนในกลุ่มเดินลงเขาทุกๆ สองวัน
ไม่ใช่ตัวอย่าง
การที่โจทย์ให้ข้อจำกัดว่านักปีนเขาทุกคน (ที่ได้รับเลือก) ต้องเริ่มออกเดินทางพร้อมกันในวันแรก ก็ช่วยให้เราแก้โจทย์ได้ง่ายขึ้นพอควรเลย เพราะถ้าเราลองยกข้อจำกัดนี้ทิ้งไป (เพื่อให้ตรงกับปัญหาในโลกจริงมากขึ้น?) เราจะเห็นว่าเราสามารถจัดกลุ่มนักปีนเขาที่น่าสนใจหลากหลายได้มากกว่านี้ จนทำให้บางกรณีถือว่าว่าสามารถปีนเขาได้สำเร็จ เช่นสมมติให้ภูเขาสูง $n=5$ และเรามีนักปีนเขาแค่สองคนที่กินข้าววันละหนึ่งกล่องและแบกข้าวได้ 6 กล่องทั้งคู่ เราอาจได้กำหนดการปีนเขาดังนี้
- ให้ทั้งคู่ออกเดินทางพร้อมกัน โดยหยิบข้าวกล่องกันไปทั้งสองคนจนเต็มกระเป๋า
- ให้คนที่สองเดินทางกลับในวันที่ 2 นั่นคือ คนแรกจะมีข้าวกล่อง 6 กล่องสำหรับเดินทางขึ้นเขาต่อ
- คนที่สองจะกลับถึงฐานในวันที่ 4 และคนแรกจะถึงยอดเขาในวันที่ 5 (เหลือข้าวกล่อง 3 กล่อง)
- ให้คนที่สองเดินขึ้นเขาอีกครั้งในวันที่ 6 (นั่นก็คือกลับไปเตรียมข้าวกล่องที่ฐานเพิ่มอีกชุดนึงนั่นเอง)
- คนที่สองเดินทางไปพบคนแรกวันที่ 8 ซึ่งเป็นวันที่ข้าวกล่องหมดพอดี
- ทั้งสองลงจากเขากลับมาที่ฐานได้สำเร็จ
แต่สำหรับโจทย์ต้นฉบับข้อนี้แล้วจะถือว่าปืนเขาไม่สำเร็จ
แล้วงั้นเราจะแก้โจทย์นี้อย่างไรดี?
ข้อสังเกตแรก (ที่อาจไม่ได้ส่งผลให้โจทย์ง่ายลงแต่อย่างใด แค่ทำให้คิดเลขได้ง่ายเท่านั้น) คือว่านักปีนเขาแต่ละคนนั้น ไม่จำเป็นต้องกินเสบียงที่ตัวเองแบกมาก็ได้ แต่สามารถไปกินเสบียงของคนอื่นได้อยู่ดี เพราะอย่างไรซะคนที่หันหลังกลับก็ต้องยกเสบียงที่เหลือให้คนอื่นๆ อยู่แล้ว
ถ้าเราลองนั่งคิดต่ออีกหน่อย จะได้ข้อสังเกตที่สำคัญเพิ่มมาว่า นักปีนเขาที่มีโอกาสเป็นผู้พิชิตยอดเขาได้สำเร็จ จะต้องเป็นคนที่สามารถเดินทางด้วยตนเองได้อย่างน้อย $n$ วันสำหรับขาลงเขา (ส่วนขาขึ้นเขานั้นสามารถให้คนอื่นช่วยแบกข้าวไปให้ได้)
และนอกจากนี้เราอาจได้ข้อสังเกตอีกอย่างว่า สำหรับนักปีนเขาที่ต้องการอาหารเป็นปริมาณเท่ากันในแต่ละวัน การเลือกนักปีนเขาที่แบกข้าวไปได้เยอะกว่านั้นดีกว่าเสมอ (นั่นคือสำหรับนักปีนเขา $i,j$ ที่ $c_i=c_j$ ถ้า $s_i<s_j$ แล้วเราควรเลือกพิจารณา $j$ ก่อนเสมอ)
ดังนั้นถ้าเราลองนำเอาข้อสังเกตเหล่านี้กับตัวอย่างที่ทดๆ ไว้มาเขียนเป็นแผนภาพกำหนดการปีนเขา ก็น่าจะได้อะไรประมาณนี้
กำหนดการปีนเขาในตัวอย่างที่สาม ที่ต้องใช้นักปีนเขาห้าคนช่วยกัน
นั่นก็คือเราสามารถมองปัญหานี้เป็นการเรียกตัวเองได้ โดยให้ปัญหาแต่ละชั้นเป็นภูเขาที่สูงลดลงไปเรื่อยๆ โดยที่คนสุดท้ายประจำแต่ละชั้นจะต้องสามารถลงเขาด้วยตัวเองได้สำเร็จ ส่วนขาขึ้นหากปีนเองได้ไม่ถึงยอดก็ขอความช่วยเหลือจากนักปีนเขาคนก่อนหน้าให้แบกเสบียงข้าวกล่องให้นั่นเอง
ดังนั้นปัญหาก็จะเหลือแค่การคำนวณวันเวลาว่า ภูเขาลูกเล็กๆ สำหรับแต่ละคนนั้นต้องใช้เวลาปีนกี่วันจึงจะถึงยอด และทำให้เราได้โค้ดออกมาหน้าตาประมาณนี้
from math import inf
from copy import deepcopy
from collections import namedtuple, defaultdict
Hiker = namedtuple('Hiker', 'name capacity rate')
Order = namedtuple('Order', 'hiker days carry')
def ceil_div(numerator, denominator):
quotient, remainder = divmod(numerator, denominator)
return quotient + (remainder > 0)
def scoring(plan, need=0):
if plan is None:
return inf, inf
return len(plan), need + sum(order.carry for order in plan)
def iterate_strongest_by_rate(groups):
for rate in groups.keys():
altered_groups = deepcopy(groups)
hiker = altered_groups[rate].pop()
if not altered_groups[rate]:
del altered_groups[rate]
yield altered_groups, hiker
def aux(days, groups, need=0, this_plan=[], best_plan=None):
if scoring(best_plan) < scoring(this_plan, need):
return best_plan
if days == 0:
return min(best_plan, this_plan, key=scoring)
for re_groups, hiker in iterate_strongest_by_rate(groups):
if hiker.capacity < days*hiker.rate:
continue
total_need = 2*days*hiker.rate + need
actual_carry = min(total_need, hiker.capacity)
re_plan = this_plan + [Order(hiker, days, actual_carry)]
accumulate_rate = sum(order.hiker.rate for order in re_plan)
re_need = total_need - hiker.capacity
re_days = ceil_div(re_need, accumulate_rate)
best_plan = aux(re_days, re_groups, re_need, re_plan, best_plan)
return best_plan
def planning(n, hikers):
groups = defaultdict(list)
for hiker in hikers:
groups[hiker.rate] += [hiker]
for group in groups.values():
group.sort(key=lambda hiker: hiker.capacity)
return aux(n, groups)
โค้ด Python ข้างต้นนี่อาจถือว่าไม่ดีเท่าไหร่ในแง่ของการแก้โจทย์แข่งขัน เพราะว่าแต่ละครั้งที่เรียกตัวเองลงไปนั้นต้องสร้างอาเรย์ใหม่ตลอด ถ้าจะเอาไปเขียนด้วย C++ เพื่อรีดประสิทธิภาพให้ได้สูงสุด อาจควรส่งพอยเตอร์อาเรย์ (หรือไม่ก็เก็บอาเรย์เป็นตัวแปรโกลบอลไปเลย) แล้วแก้ไขอาเรย์นี้ไปมาระหว่างชั้นของการเรียกตัวเองแทน
อย่างไรก็ตาม โจทย์ข้อนี้ก็ยังมีจุดอ่อนตรงอัลกอริทึมของการแก้ปัญหาอยู่ดี เพราะว่า (อย่างน้อยก็ตามวิธีข้างต้น) เราไม่สามารถแปลงมันไปเป็นกำหนดการพลวัตรได้โดยง่าย/มีประโยชน์เลย เนื่องจากว่าอย่างน้อยๆ เราก็มีลำดับการเลือกนักปีนเขาถึง $p!$ แบบเข้าไปแล้ว ซึ่งแน่นอนว่าเมื่อโจทย์ให้ $p=20$ มามันย่อมทำไม่ออกในกรณีทั่วไปแน่นอน (ไม่ว่าจะด้วยคอมพิวเตอร์ในทุกวันนี้หรือเมื่อสามสิบปีก่อนก็ตาม)
ก็ไม่น่าแปลกใจว่าทำไมถึงไม่ค่อยเห็นโจทย์แนวนี้อีก … น่าจะเรียกได้ว่าเป็นโจทย์สำหรับฝึกมือเทคนิคการเขียนโปรแกรมแบบที่ต้องเรียกตัวเองหละมั้ง ต่างจากโจทย์ในปัจจุบันที่แคร์เรื่องโครงสร้างข้อมูลและความซับซ้อนของอัลกอริทึมมากกว่านี้หลายเท่าตัว
-
ให้เล่าจริงเดี๋ยวจะยาว ก็ขอสรุปสั้นๆ แค่ว่าตอนนั้นเข้าค่ายโอลิมปิกวิชาการฟิสิกส์ดาราศาสตร์ แล้ว
สาวเพื่อนร่วมค่ายที่อยู่โอคอมฯ เอาโจทย์มาหลอกให้ทำเล่น ↩

author