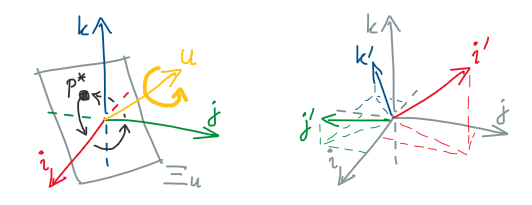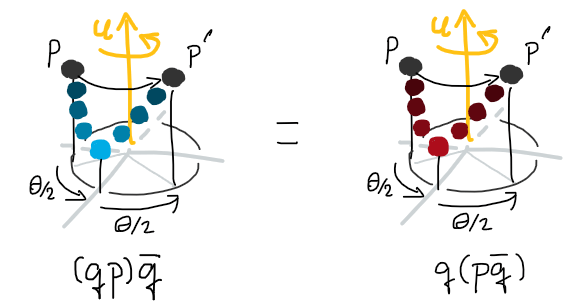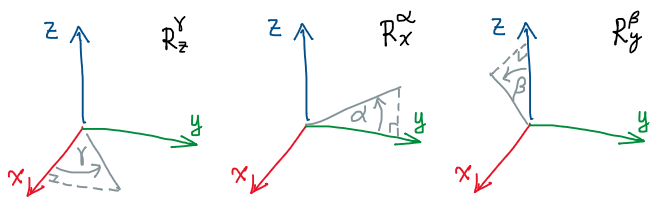
เป็นที่ทราบกันดีว่า¹ เมทริกซ์สำหรับการหมุนวัตถุในสองมิติ (หมุนรอบจุดกำเนิดด้วยมุม $\theta$ ในทิศทางทวนเข็มนาฬิกา) นั้นคือ

\[R^\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}\]

ซึ่งจากตอนที่แล้ว จะเห็นว่าเราสามารถยกระดับเมทริกซ์นี้ให้ขึ้นไปอยู่บนสามมิติได้ด้วย (ซึ่งมันจะทำให้เราได้สมบัติบางอย่างที่น่าสนใจนอกเหนือจากการหมุน โดยแลกมากับการขยายขนาดเวกเตอร์ข้อมูลด้วยการเติมเลขหนึ่งต่อท้าย) นั่นก็คือ เราจะเปลี่ยนไปเขียนเมทริกซ์ดังกล่าวเป็น

\[R_z^\theta = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

เมทริกซ์การแปลงนี้หมายความว่าเราต้องการหมุนข้อมูลรอบแกน $z$ ในทิศทางทวนเข็มนาฬิกา (หรือก็คือเราจะหมุนระนาบ $xy$ ในทิศทางที่เอาแกน $x$ หมุนเข้าหาแกน $y$ นั่นเอง)

แน่นอนว่าพอเราเห็นแบบนี้ เราก็คงเดาได้ไม่ยากว่ามันจะมีเมทริกซ์ในทำนองเดียวกันสำหรับการหมุนรอบแกนอื่นด้วย นั่นก็คือ

\[R_x^\theta = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}, \quad\quad R_y^\theta = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}\]

การหมุนรอบแกนพื้นฐานทั้งสามด้วยเมทริกซ์

ตัว $R_y$ นี่ดูเผินๆ อาจจะไม่เหมือนเพื่อนเท่าไหร่ นั่นคือเราอาจจะเข้าใจว่ามันเป็นการหมุนตามเข็มนาฬิกาจากแกน $x$ ไปหาแกน $z$ (เพราะเครื่องหมายลบสลับด้านกับเมทริกซ์อันอื่น) ซึ่งเอาจริงแล้วจะมองแบบนั้นก็ไม่ผิดเพียงแต่ว่าเราต้องมองจากแกน $-y$ เข้ามาหาจุดกำเนิดแทนด้วย อย่างไรก็ตามวิธีการมองในทำนองเดียวกับเมทริกซ์อื่น ก็คือให้มองว่ามันเป็นการหมุนทวนเข็มนาฬิกาจากแกน $z$ ไปหาแกน $x$ ต่างหาก (ซึ่งสามารถคิดอีกทางโดยโดยแปะป้ายประจำหลักและแถวในเมทริกซ์ด้วย $x,y,z$ ไล่ไปตามลำดับ แล้วจึงสลับหลักและแถวในเทริกซ์จนได้ว่าป้ายมันเรียงตัวกลายเป็น $z,x,y$ ก็ได้)

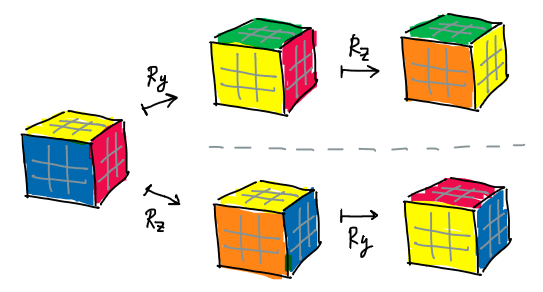
ข้อสังเกตก็คือเวลาเราหมุนสิ่งของในสามมิติเป็นจำนวนหลายครั้ง (ด้วยแกนหลายแกนที่แตกต่างกัน) ลำดับการหมุนก่อนหลังมันจะมีผล หรือพูดอีกอย่างก็คือว่าเราไม่สามารถสลับที่เมทริกซ์การหมุนได้

ตัวอย่างการหมุนที่ให้ผลลัพธ์ไม่เหมือนกันเมื่อถูกสลับลำดับ

การหมุนเป็นจำนวหลายครั้งนี้ก็ช่วนเวียนหัวอยู่ไม่น้อย แต่โชคดีที่มีทฤษฎีบทอันนึงที่รับประกันว่า ไม่ว่าเราจะหมุนสิ่งของที่สนใจในสามมิติเป็นจำนวนกี่ครั้งก็ตาม มันจะมีแกนอันนึง (ที่ไม่จำเป็นต้องเป็นแกนพื้นฐาน) ที่ทำให้เราหมุนสิ่งของเพียงครั้งเดียวแล้วได้ผลลัพธ์ปลายทางเช่นเดียวกันเลย (พูดอีกอย่างก็คือการหมุนในสามมิตินี้เป็นกรุป ซึ่งเรามีชื่อเรียกให้มันเก๋ๆ ว่า $\mathrm{SO(3)}$ โดยเฉพาะเลย)

แล้วถ้าเราเปลี่ยนไปสนใจแกนหมุนใดๆ เราจะเขียนเมทริกซ์การหมุนรอบแกนนั้นได้อย่างไร? แนวคิดง่ายๆ เพียงแค่

1. หมุนปริภูมิเพื่อจัดตำแหน่งให้แกนหมุนที่เราต้องการให้ขนานไปกับแกนพื้นฐาน
2. หมุนวัตถุที่สนใจด้วยสมการของแกนพื้นฐานที่เราเตรียมไว้
3. หมุนปริภูมิเพื่อจัดตำแหน่งให้แกนหมุนที่เราต้องการย้อนกลับไปอยู่ที่เดิม

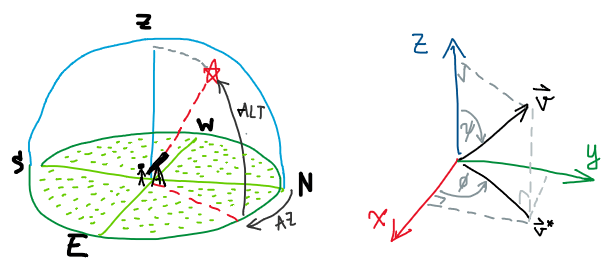
เพราะงั้นคำถามก็คือว่าแล้วเราจะระบุแกนหมุนที่ต้องการนี้อย่างไรดี? ถ้าใครชอบดูดาวก็คงจะนึกออกทันทีว่าเราก็วัดมุมจากจุดอ้างอิงไล่ตามแต่ละแกนพื้นฐานต่างๆ ไปจนถึงแกนที่เราต้องการหมุนสิ

(ซ้าย) การระบุตำแหน่งด้วยมุมทางดาราศาสตร์แบบหนึ่ง (ขวา) การระบุแกนหมุน $\vec{v}$ ในทำนองเดียวกัน

ซึ่งโจทย์ข้อนี้จะง่ายลงมากเมื่อเรานำการมองแบบดังกล่าวมาใช้ (ประยุกต์นิดหน่อยตรงจุดอ้างอิงและทิศทางของมุม) นั่นก็คือ ถ้าให้แกนหมุนเขียนแทนด้วยเวกเตอร์ $\vec{v}$ เราจะวัดมุมต่างๆ ดังนี้

• มุม $\phi$ นับจากแกน $x$ ไปหาภาพฉายของ $\vec{v}$ บนระนาบ $xy$
• มุม $\psi$ นับจากแกน $z$ ไปหาแกนหมุน $\vec{v}$ ได้เลย

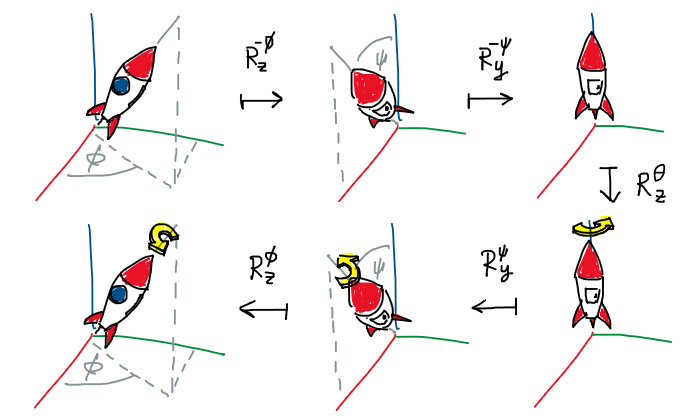
เพราะฉะนั้น ในขั้นตอนแรกที่เราอยากแปลงวัตถุให้มีแกนหมุนเป็นแกนพื้นฐาน เราก็เริ่มจากการหมุน $\vec{v}$ ด้วยมุม $-\phi$ ให้เข้ามาอยู่บนระนาบ $zx$ ก่อน (กลายเป็นเวกเตอร์ $\vec{v}’$) แล้วจึงหมุน $\vec{v}’$ ขึ้นไปด้วยมุม $-\psi$ ให้มันไปทาบบนแกน $z$ พอดี ซึ่งก็คือเขียนเป็นเมทริกซ์การแปลงได้ว่า (เตือนตรงนี้อีกซักครั้งว่าเวลาเราอ่านลำดับการทำงานของเมทริกซ์ เราอ่านไล่จากขวามาซ้าย)

\[\begin{bmatrix} \cos\psi & 0 & -\sin\psi \\ 0 & 1 & 0 \\ \sin\psi & 0 & \cos\psi \end{bmatrix} \begin{bmatrix} \cos\phi & \sin\phi & 0 \\ -\sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{bmatrix} = (R_y^{-\psi}) (R_z^{-\phi}) = (R_y^\psi)^{-1} (R_z^\phi)^{-1} = (R_z^\phi R_y^\psi)^{-1}\]

ดังนั้นเมื่อทำขั้นตอนที่สองและสามต่อจนครบ จะได้ว่าเมทริกซ์สำหรับหมุนด้วยแกน $\vec{v}$ ใดๆ ก็คือ

\[R_\vec{v}^\theta = (R_z^\phi R_y^\psi) R_z^\theta (R_z^\phi R_y^\psi)^{-1} \tag{1} \label{eq:five-rotations}\]

การหมุนห้าครั้งในแกนพื้นฐานเพื่อสร้างการหมุนที่ต้องการในแกนใดๆ

ตรงนี้ถ้าใครขยันหน่อยอาจจะลองคูณเมทริกซ์ $\eqref{eq:five-rotations}$ ออกมาดูได้ ซึ่งมันน่าจะกินพื้นที่กระดาษทดอยู่พอสมควรเลย อย่างไรก็ตาม เราจะกลับไปนิยามเวกเตอร์แกนหมุนให้ชัดเจนขึ้นว่ามันคือ

\[\vec{v} = \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix}, \quad\quad \vec{v}^\ast = \begin{bmatrix} v_x \\ v_y \\ 0 \end{bmatrix}\]

ซึ่งทำให้เราได้

\[\begin{array}{l} \cos\phi = \frac{v_x}{\norm{\vec{v}^\ast}}, & \sin\phi = \frac{v_y}{\norm{\vec{v}^\ast}}; \\ \cos\psi = \frac{v_z}{\norm{\vec{v}}}, & \sin\psi = \frac{\norm{\vec{v}^\ast}}{\norm{\vec{v}}}; \\ \norm{\vec{v}^\ast}^2 = v_x^2 + v_y^2, & \norm{\vec{v}}^2 = v_x^2 + v_y^2 + v_z^2; \end{array}\]

นอกจากนี้ ถึงแม้ว่าแกนหมุน $\vec{v}$ ที่เราสนใจจะมีค่าเป็นอย่างไรก็ได้ แต่ในการคำนวณจริงมันจะง่ายลงมากเมื่อเราสนใจแกนหมุนที่ถูกปรับค่าให้เป็นมาตรฐานแล้ว เราจะเปลี่ยนไปใช้แกนหมุน $\vec{u}$ ที่เป็นเวกเตอร์หนึ่งหน่วยแทน นั่นคือ

\[\vec{u} = \frac{\vec{v}}{\norm{v}}\]

เมื่อใช้ความรู้เหล่านี้ช่วยกระจายผลคูณเมทริกซ์ใน $\eqref{eq:five-rotations}$ คราวนี้จะได้คำตอบที่สั้นลงเหลือแค่

\[R_\vec{v}^\theta = R_\vec{u}^\theta = \begin{bmatrix} \cos\theta + u_x^2(1{-}\cos\theta) & u_xu_y(1{-}\cos\theta) - u_z\sin\theta & u_xu_z(1{-}\cos\theta) + u_y\sin\theta \\ u_yu_x(1{-}\cos\theta) + u_z\sin\theta & \cos\theta + u_y^2(1{-}\cos\theta) & u_yu_z(1{-}\cos\theta) - u_x\sin\theta \\ u_zu_x(1{-}\cos\theta) - u_y\sin\theta & u_zu_y(1{-}\cos\theta) + u_x\sin\theta & \cos\theta + u_z^2(1{-}\cos\theta) \end{bmatrix} \tag{2} \label{eq:rotation-matrix}\]

เอาจริงๆ การจัดรูปให้ได้ออกมาแบบนี้ก็ไม่ง่ายเท่าไหร่ แต่ข้อสังเกตสำคัญขณะที่กำลังจัดรูปอยู่นั้น ก็คือแต่ละช่องในเมทริกซ์มันจะมีความคล้ายกันเป็นสองกลุ่มใหญ่ กลุ่มแรกคือช่องที่ไม่ใช่ช่องทะแยงมุมที่จัดรูปง่ายหน่อย ซึ่งจะเห็นว่ามันแทบจะสะท้อนฝั่งตรงข้ามมาเลย (เปลี่ยนแค่เครื่องหมาย) ส่วนอีกกลุ่มคือบรรดาช่องทะแยงมุมที่ตอนเริ่มจัดรูปอาจดูว่ามันไม่ได้คล้ายกันเท่าใดนัก แต่ว่ามันต้องสามารถจัดรูปออกมาได้หน้าตาเดียวกันแน่ๆ เพราะว่าเราอาจเปลี่ยนเมทริกซ์ตั้งต้นที่ $\eqref{eq:five-rotations}$ เพื่อหมุนเข้าแกนพื้นฐานแกนอื่นก็ได้ (และมันก็จะได้เมทริกซ์ที่หน้าตาเหมือนกันเพียงแค่เปลี่ยนชื่อตัวแปรและสลับตำแหน่งหลัก/แถวเมทริกซ์เท่านั้น)

ทั้งนี้ เมทริกซ์การหมุนแบบที่ใช้แกนพื้นฐานตามลำดับใน $\eqref{eq:five-rotations}$ น่าจะนับว่าช่วยให้กระจายผลคูณแล้วจัดรูปเป็น $\eqref{eq:rotation-matrix}$ ได้ง่ายที่สุดแล้ว(มั้ง) นั่นคือเราอาจเปลี่ยนไปใช้เมทริกซ์การหมุนพื้นฐานอื่นๆ ก็ได้ ซึ่งท้ายที่สุดแล้วเราจะสามารถจัดรูปให้มันเป็นแบบข้างต้นได้เสมอ เพียงแต่ว่าระหว่างทางอาจจะเจอพจน์ประหลาดๆ โผล่มาเยอะกว่านี้จนถอดใจยอมแพ้ไม่จัดรูปต่อแล้ว ถถถถถถ

---

เมทริกซ์การหมุนข้างต้นนี้ก็ดูเป็นระเบียบดี แต่เอาตามตรงเลยก็คือมันค่อนข้างใหญ่เทอะทะพอสมควร เพราะงั้นคำถามที่ตามมาก็คงหนีไม่พ้นว่าเราจะสามารถอธิบายการหมุนให้มันเรียบง่าย/สวยงามกว่านี้ได้อีกมั้ย? ซึ่งคำตอบก็คือมีอีกวิธีหนึ่งที่เขียนเป็นสมการได้สั้นกระชับกว่านี้² แต่รายละเอียดอันซับซ้อนของมันก็อาจจะทำให้สมองระเบิดได้เลย เพราะเราจะไปพึ่งพาจำนวนเชิงซ้อนแบบสี่มิติเพื่อช่วยอธิบายการหมุนดังกล่าวในสามมิติ! (เอาจริงๆ แล้วส่วนตัวก็ยังมองภาพไม่ค่อยออกเท่าไหร่ เพราะงั้นจะขอเริ่มด้วยการเสกทุกอย่างขึ้นมาให้เห็นว่ามันทำงานได้ก่อน)

เรานิยามควอเทอร์เนียน (quaternion หรือจำนวนเชิงซ้อนสี่มิติ) ในทำนองเดียวกันกับจำนวนเชิงซ้อน $a+b\mathbf{i}$ ที่เราคุ้นเคยกันดี ซึ่งก็คือเราจะเพิ่มส่วนจินตภาพที่ตั้งฉากกับส่วนจริงอีกสองแกน³ เช่นนี้

\[\mathbf{h} = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}\]

โดยที่

\[\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = \mathbf{ijk} = -1\]

ข้อห้ามสำคัญก็คือจำนวนควอเทอร์เนียนไม่มีสมบัติสลับที่การคูณ ซึ่งดูเผินๆ อาจคิดว่าเป็นอะไรที่ขัดสามัญสำนึกพอควร แต่จริงๆ แล้วสมบัตินี้คือความเป็นธรรมชาติของการหมุนด้วยแกนมากกว่าหนึ่งแกนเลยหล่ะ (เทียบเคียงได้กับเมทริกซ์การแปลงที่ลำดับการทำงานก่อนหลังมีผล)

ถัดมาเราจะระลึกถึงเทคนิคทางคณิตศาสตร์ที่น่าสนใจอันนึง นั่นคือการ “แซนด์วิช” ประกบวัตถุทางคณิตศาสตร์ที่เราสนใจด้วยคู่ของวัตถุคู่หนึ่งที่มีความคล้ายคลึงกัน อย่างที่เราได้เห็นไปข้างต้นแล้วใน $\eqref{eq:five-rotations}$ ที่เราประกบเมทริกซ์ $R_z^\theta$ ด้วย $(R_z^\phi R_y^\psi)$ กับ $(R_z^\phi R_y^\psi)^{-1}$ หรือในเรื่องอื่นๆ อีกมากมาย เช่น การแยกเมทริกซ์ลักษณะเฉพาะ ที่เราแยกเมทริกซ์ได้เป็น $\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{-1}$

ดังนั้นสิ่งที่เราจะเสกขึ้นมา ก็คือการคูณควอเทอร์เนียนที่ประกบหน้าหลัง เช่นนี้

\[\mathbf{p}' = \mathbf{q}\mathbf{p}\mathbf{\bar{q}} \tag{3} \label{eq:quaternion-conjugation}\]

โดยที่

• $\mathbf{p} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ แทนตำแหน่งจุดข้อมูลตั้งต้นก่อนหมุน (เทียบได้กับเวกเตอร์ $\vec{p}=[x,y,z]^T$)
• $\mathbf{p}’ = x’\mathbf{i} + y’\mathbf{j} + z’\mathbf{k}$ แทนตำแหน่งผลลัพธ์จุดข้อมูลหลังจากที่โดนหมุนไปเรียบร้อยแล้ว
• $\mathbf{q} = q_r + q_x\mathbf{i} + q_y\mathbf{j} + q_z\mathbf{k}$ เป็นควอเทอร์เนียนหนึ่งหน่วยใดๆ ที่มาพร้อมกับคู่สังยุคของมัน (นั่นก็คือ $\mathbf{q}\mathbf{\bar{q}} = \norm{\mathbf{q}}^2 = 1$)

ทั้งนี้ เมื่อเรานึกถึงการคูณควอเทอร์เนียนโดยทั่วไป (หรือจะนึกถึงแค่จำนวนเชิงซ้อนก็ได้) ผลลัพธ์หลังการคูณเสร็จมักจะติดพจน์ทั้งส่วนจริงและส่วนจินตภาพมาด้วยเสมอ อย่างไรก็ตาม เมื่อเราคูณกระจาย $\eqref{eq:quaternion-conjugation}$ พร้อมจัดรูปอีกนิดหน่อย จะเห็นว่าผลลัพธ์คือ

\[\begin{align} \mathbf{p}' = 0 &+ \left( (q_r^2{+}q_x^2{-}q_y^2{-}q_z^2)x + 2(q_xq_y{-}q_rq_z)y + 2(q_xq_z{+}q_rq_y)z \right) \mathbf{i} \\ &+ \left( 2(q_yq_x{+}q_rq_z)x + (q_r^2{-}q_x^2{+}q_y^2{-}q_z^2)y + 2(q_yq_z{-}q_rq_x)z \right) \mathbf{j} \\ &+ \left( 2(q_zq_x{-}q_rq_y)x + 2(q_zq_y{+}q_rq_x)y + (q_r^2{-}q_x^2{-}q_y^2{+}q_z^2)z \right) \mathbf{k} \end{align} \tag{4} \label{eq:quaternion-expand}\]

นั่นก็คือส่วนจริงในควอเทอร์เนียนถูกหักล้างกันเองหายไปจนหมด หรือพูดอีกอย่างได้ว่า ถึงแม้ระหว่างทางเราจะทำงานกับตัวเลขสี่มิติ แต่ผลลัพธ์ปลายทางนั้นจะหดลงมาเหลือเพียงสามมิติอยู่ดี นี่ทำให้เราสามารถมอง $\eqref{eq:quaternion-expand}$ ในเชิงเมทริกซ์สามมิติได้เช่นกัน ซึ่งก็คือเราจะเขียนมันให้อยู่ในรูป $\vec{p}’ = R_\mathbf{q}\vec{p}$ โดยที่

\[R_\mathbf{q} = 2\begin{bmatrix} q_r^2+q_x^2 - \frac12 & q_xq_y-q_rq_z & q_xq_z+q_rq_y \\ q_yq_x+q_rq_z & q_r^2+q_y^2 - \frac12 & q_yq_z-q_rq_x \\ q_zq_x-q_rq_y & q_zq_y+q_rq_x & q_r^2+q_z^2 - \frac12 \end{bmatrix} \tag{5} \label{eq:quaternion-matrix}\]

ถึงตรงนี้เราคงเห็นได้ไม่ยากว่าเมทริกซ์ $\eqref{eq:rotation-matrix}$ กับ $\eqref{eq:quaternion-matrix}$ นั้นมีโครงสร้างคล้ายกันมากพอควร และเพราะว่าทั้งสองเมทริกซ์นั้นทำงานและให้ผลลัพธ์ออกมาเหมือนกัน เราจึงอาจเดาได้ว่าเมทริกซ์ทั้งสองตัวนี้ก็ควรจะมีหน้าตาเหมือนกันด้วย (ผ่านการจัดรูป/เปลี่ยนค่าตัวแปร) ดังนั้นเราจะย้อนกลับไปจัดรูปเมทริกซ์ $\eqref{eq:rotation-matrix}$ ต่ออีกนิดหน่อย โดยแอบเปิดดูเฉลยเดาว่าเราไม่ได้ต้องการทำงานบนมุม $\theta$ แต่ลดลงมาครึ่งนึงเป็นมุม $\theta/2$ ต่างหาก ดังนั้นเราจะใช้เอกลักษณ์ตรีโกณมิติต่างๆ เหล่านี้

\[\cos\theta = 2\cos^2\frac\theta2 - 1, \quad 1{-}\cos\theta = 2\sin^2\frac\theta2, \quad \sin\theta = 2\sin\frac\theta2\cos\frac\theta2\]

ไปจัดรูป $\eqref{eq:rotation-matrix}$ ให้กลายเป็น

\[R_\vec{u}^\theta = 2\begin{bmatrix} \cos^2\frac\theta2 + u_x^2\sin^2\frac\theta2 - \frac12 & u_xu_y\sin^2\frac\theta2 - u_z\sin\frac\theta2\cos\frac\theta2 & u_xu_z\sin^2\frac\theta2 + u_y\sin\frac\theta2\cos\frac\theta2 \\ u_yu_x\sin^2\frac\theta2 + u_z\sin\frac\theta2\cos\frac\theta2 & \cos^2\frac\theta2 + u_y^2\sin^2\frac\theta2 - \frac12 & u_yu_z\sin^2\frac\theta2 - u_x\sin\frac\theta2\cos\frac\theta2 \\ u_zu_x\sin^2\frac\theta2 - u_y\sin\frac\theta2\cos\frac\theta2 & u_zu_y\sin^2\frac\theta2 + u_x\sin\frac\theta2\cos\frac\theta2 & \cos^2\frac\theta2 + u_z^2\sin^2\frac\theta2 - \frac12 & \end{bmatrix}\]

ซึ่งจะทำให้เราเห็นได้ทันทีว่า $R_\vec{u}^\theta = R_\mathbf{q}$ เมื่อ

\[\begin{array}{l} q_r = \cos\frac\theta2, & q_x = u_x\sin\frac\theta2, \\ q_y = u_y\sin\frac\theta2, & q_z = u_z\sin\frac\theta2; \end{array}\]

และทำให้เราสรุปได้ว่า สมการ $\eqref{eq:quaternion-conjugation}$ นั้นก็สามารถคำนวณการหมุนในสามมิติรอบแกน $\vec{u}$ ด้วยมุม $\theta$ ได้เช่นกัน โดยเราจะต้องตระเตรียมควอเทอร์เนียน $\mathbf{q}$ เพื่อทำงานระหว่างทาง ดังนี้

\[\begin{align} \mathbf{q} &= \cos\frac\theta2 + (u_x\mathbf{i} + u_y\mathbf{j} + u_z\mathbf{k})\sin\frac\theta2 \\ &= \cos\frac\theta2 + \frac{v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}}{\norm{\vec{v}}} \sin\frac\theta2 \tag{6} \label{eq:rotation-quaternion} \end{align}\]

---

แล้วทำไมควอเทอร์เนียนมันถึงหมุนสิ่งของในสามมิติได้ เราจะอธิบายให้เห็นภาพการทำงานของมันได้อย่างไร มุมแค่ครึ่งเดียวมาจากไหน อะไรคือแนวคิดเบื้องหลังของเรื่องราวทั้งหมดนี้ … คำถามเหล่านี้ก็ดูน่าขย่มขวัญพอสมควรเลย เพราะนัยหนึ่งก็เหมือนกับว่ามันร้องขอให้เรามองภาพสี่มิติให้ออก!?

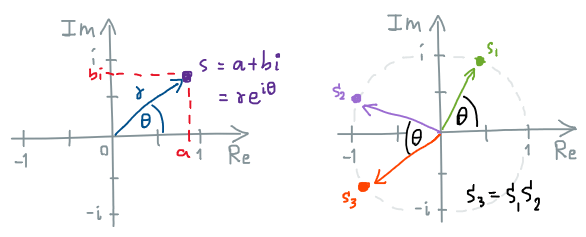
แต่จริงๆ แล้วเราอาจลองอธิบายง่ายๆ (ที่อาจไม่ถูกต้องแม่นยำมากนัก) เพื่อให้เห็นภาพรวมได้ว่า เราได้แนวคิดของควอเทอร์เนียนมาจากจำนวนเชิงซ้อน

\[\mathbf{s} = a + b\mathbf{i}\]

โดยที่มี $\mathbf{i}$ เป็นหน่วยจินตภาพที่มีสมบัติว่า $\mathbf{i}^2 = -1$ เราจะเห็นว่าการบวก(และลบ)จำนวนเชิงซ้อนสองตัวก็ง่ายๆ นั่นคือเอาส่วนจริงมาบวกกันแล้วเก็บผลลัพธ์ลงส่วนจริง และเอาส่วนจินตภาพมาบวกกันแล้วเก็บผลลัพธ์ลงส่วนจินตภาพ แค่นั้นเอง

แต่การคูณจำนวนเชิงซ้อนกลับมีความยุ่งยากกว่ามากๆ เพราะว่าส่วนจริงกับส่วนจินตภาพจะถูกนำมาใช้คำนวณข้ามฝั่งกันไปมา โชคดีที่เราสามารถเปลี่ยนไปเขียนจำนวนเชิงซ้อนในรูปเชิงมุมได้ นั่นก็คือ

\[\mathbf{s} = r(\cos\varphi + \mathbf{i}\sin\varphi) = re^{\mathbf{i}\varphi}\]

การตีความจำนวนเชิงซ้อนให้กลายเป็นเลขยกกำลังฐานธรรมชาติ $re^{\mathbf{i}\varphi}$ เช่นนี้มีความสำคัญมาก เพราะมันจะทำให้เรามองการคูณจำนวนเชิงซ้อนสองตัวว่าเป็นการนำรัศมีมาคูณกัน และนำมุมมาบวกกัน แยกกออกจากกันไม่ต้องคิดข้ามไปข้ามมานั่นเอง

\[\mathbf{s}_1 \mathbf{s}_2 = r_1r_2e^{\mathbf{i}(\varphi_1+\varphi_2)}\]

พูดอีกอย่างก็คือ จำนวนเชิงซ้อนก็เป็นวัตถุทางคณิตศาสตร์แบบหนึ่งที่เอาไว้ระบุตำแหน่งสิ่งของในสองมิติ โดยมันมีทั้งสมบัติการเลื่อนตำแหน่งและการย่อขยายขนาดแบบเดียวกับเวกเตอร์สองมิตินั่นแหล่ะ ที่เพิ่มเติมขึ้นมาคือสมบัติการหมุนผ่านการคูณกันของจำนวนเชิงซ้อนสองตัว (เวกเตอร์ต้องไปใช้เมทริกซ์มาช่วยหมุน) เพราะงั้นเราอาจสรุปได้ว่า ระบบจำนวนเชิงซ้อนก็คือระบบที่เชี่ยวชาญด้านการหมุนเป็นพิเศษนั่นเอง

การคูณคือการหมุนในจำนวนเชิงซ้อน

แต่จำนวนเชิงซ้อนนี้ก็ทำงานได้แค่บนสองมิติเท่านั้น แล้วถ้าเราอยากจะหมุนของในสามมิติบ้างหล่ะ? ขั้นแรกสุดเราอาจลองเพิ่มหน่วยจินตภาพ $\mathbf{j}$ ที่ตั้งฉากกับทั้ง $1$ และ $\mathbf{i}$ เข้าไป นี่ทำให้เรามีจำนวนเชิงซ้อนสามมิติ $a+b\mathbf{i}+c\mathbf{j}$ ที่ดูคร่าวๆ ก็เหมือนว่าจะหมุนอะไรง่ายๆ ตามแกนพื้นฐานได้บ้าง แต่ก็ยังไม่สามารถหมุนได้ทุกจุดด้วยแกนใดๆ ในปริภูมิสามมิติได้ตามต้องการ

นี่คือจุดที่ Hamilton ติดอยู่นานนับทศวรรษ จนกระทั่ง 1843 เขาก็คิดออกระหว่างเดินเล่นริมแม่น้ำ⁴ ว่าต้องใช้หน่วยจินตภาพ $\mathbf{k}$ (ที่ตั้งฉากกับหน่วยจินตภาพอื่นๆ) เพิ่มอีกหนึ่งตัว จึงทำให้ได้จำนวนเชิงซ้อนสี่มิติว่า

\[\mathbf{h} = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}\]

เพียงแต่ว่าคราวนี้เราจะไม่ระบุตำแหน่งสิ่งของในสามมิติด้วยตัวแปร $a$ ซึ่งเป็นส่วนจริงแล้ว (เพราะมันมีพฤติกรรมไม่เหมือนกับส่วนจินตภาพอื่นๆ เลย) แต่จะเปลี่ยนไปใช้ $b,c,d$ เพื่อระบุตำแหน่งสิ่งของตามพิกัด $x,y,z$ แทนตามลำดับ – อนึ่ง ในที่นี้จะให้ $\Xi_\mathbf{i}$ เป็นระนาบที่ตั้งฉากกับหน่วยจินตภาพ $\mathbf{i}$ ณ จุดกำเนิด หรือก็คือทุกจุดที่อยู่บนระนาบนี้จะต้องมีค่า $x$ เป็นศูนย์นั่นเอง (แน่นอนว่าเรานิยาม $\Xi_\mathbf{u}$ สำหรับหน่วยจินตภาพ $\mathbf{u}$ อื่นๆ ในทำนองเดียวกันอีกด้วย)

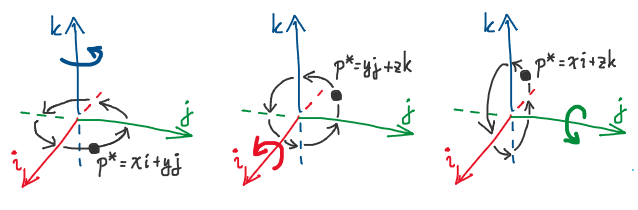
การมีหน่วยจินตภาพสามหน่วยเช่นนี้ก็ทำให้เราสามารถหมุนจุดที่อยู่บนระนาบที่ตั้งฉากกับแกนพื้นฐานได้แล้ว เช่น ถ้าเราอยากจะหมุนจุด $\mathbf{p}^\ast = x\mathbf{i}+y\mathbf{j}$ รอบแกน $\mathbf{k}$ (เพราะว่า $\mathbf{p}^\ast$ นั้นอยู่บนระนาบ $\Xi_\mathbf{k}$ พอดี) ด้วยมุม $\theta$ ในทิศทางทวนเข็มนาฬิกา เราก็แค่เอา $\cos\theta+\mathbf{k}\sin\theta$ คูณเข้าไปทางด้านซ้ายของ $\mathbf{p}^\ast$ ก็พอ (หากคูณทางขวาจะได้การหมุนตามเข็มนาฬิกามาแทน) นั่นก็คือ

\[\mathbf{p}' = (\cos\theta + \mathbf{k}\sin\theta) \mathbf{p}^\ast = (x\cos\theta - y\sin\theta)\mathbf{i} + (x\sin\theta + y\cos\theta)\mathbf{j}\]

การหมุนรอบหน่วยจินตภาพพื้นฐานทั้งสาม

ถึงตอนนี้ก็จะเหลือแค่สองประเด็น ประเด็นแรกคือกรณีที่จุดที่ต้องการหมุนไม่ได้อยู่บนระนาบ และประเด็นที่สองคือกรณีที่แกนหมุนไม่ใช่แค่แกนพื้นฐาน หากเราสามารถอธิบายทั้งสองประเด็นนี้ได้ก็จะได้การหมุนในสามมิติที่ครบถ้วนสมบูรณ์

เราจะดูประเด็นที่สองกันก่อน นั่นคือเมื่อเราต้องการหมุนจุดที่สนใจด้วยแกนใดๆ (แต่ว่าจุดที่ถูกหมุนจะต้องอยู่บนระนาบที่ตั้งฉากกับแกนนั้น) ขั้นแรกก็คือเราจะนิยามแกนหมุนที่สนใจนี้ผ่านหน่วยจินตภาพ $\mathbf{u}$ (มีค่า $\norm{\mathbf{u}}=1$) ที่เราสร้างขึ้นมาผ่านการนำหน่วยจินตภาพพื้นฐานอื่นๆ มาประกอบรวมกัน ดังนี้

\[\mathbf{u} = u_i\mathbf{i} + u_j\mathbf{j} + u_k\mathbf{k} \tag{7} \label{unit-imaginary}\]

จากจุด $\mathbf{p}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}$ ทั้งหมดในปริภูมิสามมิติ จะได้ว่าจุดที่อยู่บนระนาบ $\Xi_\mathbf{u}$ พอดีก็คือ

\[\begin{align} \mathbf{p}^\ast &= \mathbf{p} - (\mathbf{p}\cdot\mathbf{u})\mathbf{u} \\ &= (x - u_i\mathbf{p}\cdot\mathbf{u})\mathbf{i} + (y - u_j\mathbf{p}\cdot\mathbf{u})\mathbf{j} + (z - u_k\mathbf{p}\cdot\mathbf{u})\mathbf{k} \end{align}\]

โดยที่เราเขียนย่อ $\mathbf{p}\cdot\mathbf{u} = u_ix + u_jy + u_kz$ ดังนั้นตำแหน่งที่ได้หลังการหมุนก็คือ

\[\begin{align} \mathbf{p}' &= (\cos\theta + \mathbf{u}\sin\theta)\mathbf{p}^\ast \\ &= \mathbf{p}^\ast\cos\theta + \mathbf{u}\mathbf{p}^\ast\sin\theta \\ &= \mathbf{p}^\ast\cos\theta + \big( (u_yz{-}u_zy)\mathbf{i} + (u_zx{-}u_xz)\mathbf{j} + (u_xy{-}u_yx)\mathbf{k} \big)\sin\theta \end{align}\]

สังเกตว่าทั้ง $\mathbf{p}^\ast$ และ $\mathbf{p}’$ นั้นไม่มีส่วนจริงเลย ซึ่งก็คือเราหมุนจุดบางจุดให้ยังอยู่ในสามมิติได้เสมอ

การแก้ประเด็นนี้ได้สำเร็จ ยังส่งผลให้เรารู้อีกว่าเราไม่จำเป็นต้องใช้แค่หน่วยจินตภาพ $\mathbf{i,j,k}$ เพื่อเป็นพื้นฐานของแกนสามมิติเท่านั้น แต่สามารถเลือกใช้หน่วยจินตภาพ $\mathbf{i’,j’,k’}$ ชุดใดๆ ที่ตั้งฉากกันแทนก็ได้ (แล้วเราก็เปลี่ยนไปวัดตำแหน่งจุดข้อมูลต่างๆ โดยอ้างอิงกับชุดของแกนใหม่นี้ที่เราเลือกแทน) อย่างไรก็ตาม หน่วยจินตภาพทุกตัวจะต้องมีจุดกำเนิดเดียวกันเสมอ

(ซ้าย) หมุนจุด $\mathbf{p}^\ast$ บนระนาบ $\Xi_\mathbf{u}$ รอบแกน $\mathbf{u}$ (ขวา) หน่วยจินตภาพชุดอื่นๆ ที่สามารถใช้แทน $\mathbf{ijk}$ ได้

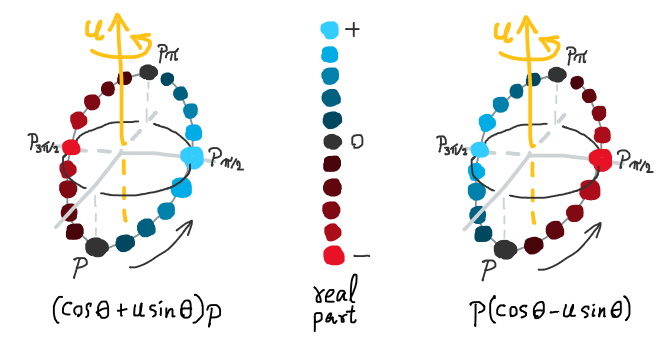
ทีนี้ย้อนกลับไปดูประเด็นที่แรกที่เราอยากหมุนจุด $\mathbf{p}$ ใดๆ ก็ได้ในปริภูมิ (ไม่ใช่แค่เฉพาะจุดที่อยู่บนระนาบ $\Xi_\mathbf{u}$) สังเกตว่าหากเราเลือกหมุนด้วยมุม $\theta$ ตามความเคยชิน การคูณควอเทอร์เนียน $(\cos\theta + \mathbf{u}\sin\theta)\mathbf{p}$ จะมีผลข้างเคียงตามมาดังนี้

• มีส่วนจริงโผล่เข้ามาในผลลัพธ์ (ผลลัพธ์ไม่ได้อยู่แค่ในสามมิติอีกต่อไปแล้ว)
• ส่วนจินตภาพในผลลัพธ์จะอยู่ห่างจากระนาบ $\Xi_\mathbf{u}$ ด้วยระยะทางไม่คงที่ (ระยะห่างขึ้นอยู่กับค่า $\theta$​)
• เส้นโค้งผลลัพธ์จะเป็นวงรีในสามมิติ (อย่างไรก็ตาม เมื่อฉายโค้งนี้ลงระนาบ $\Xi_\mathbf{u}$ จะยังได้วงกลมอยู่)

ผลข้างเคียงพวกนี้สามารถเห็นได้ชัดเพียงแค่เราพิจารณาการหมุนด้วยมุมง่ายๆ เช่นการหมุนด้วยมุม $\pi$ จะให้ผลลัพธ์ $\mathbf{p_\pi}$ ว่าเป็นภาพสะท้อนของ $\mathbf{p}$ ผ่านจุดกำเนิด (หรือก็คือ $\mathbf{p}+\mathbf{p_\pi}=0$) นั่นหมายความว่าทั้ง $\mathbf{p}$ และ $\mathbf{p_\pi}$ จะอยู่คนละฟากของ $\Xi_\mathbf{u}$ และมันจะต้องมีบางมุมที่ทำให้ผลลัพธ์การหมุนวิ่งผ่านระนาบ $\Xi_\mathbf{u}$ พอดี แน่นอนว่าเราคงเดาได้ไม่ยากว่ามันคือมุม $\pi/2$ (และ $-\pi/2$) และเราจะเห็นได้อีกว่า $\mathbf{p_{\pi/2}}$ นั้นจะต้องมีส่วนจริงโผล่เข้ามา เพราะว่ามันจะมีบางพจน์ที่คูณกันแล้วได้หน่วยจินตภาพพื้นฐานยกกำลังสอง (ยิ่งไปกว่านั้น $\mathbf{p_{\pi/2}}$​ จะมีส่วนจริงที่มีค่าห่างจากศูนย์มากที่สุดในบรรดามุมการหมุนทั้งหมดอีกด้วย)

ตัวอย่างผลลัพธ์การหมุนจุด $\mathbf{p}$ ด้วยมุมต่างๆ โดยให้สีประจำจุดแทนค่าของส่วนจริงที่โผล่เข้ามา

การจะได้มาซึ่งการหมุนในสามมิติที่ถูกต้องสมบูรณ์ ก็ขอแค่เรากำจัดผลข้างเคียงอันไม่พึงประสงค์เหล่านี้ทิ้งไปให้หมด นั่นคือเราอยากให้ผลลัพธ์ไม่มีส่วนจริงโผล่เข้ามา และมีระยะห่างจากระนาบการหมุนเป็นค่าคงที่ ซึ่งถ้าเราอยากได้แค่นี้จริงๆ ก็ไม่ยาก ทางนึงที่ทำได้ก็คือเริ่มจากให้ $\mathbf{p}^\ast$ เป็นภาพฉายจุด $\mathbf{p}$ บนระนาบ $\Xi_\mathbf{u}$ ต่อมาเราก็หมุนจุด $\mathbf{p}^\ast$ ด้วยมุม $\theta$ รอบแกนหมุน $\mathbf{u}$ ให้กลายเป็นจุด $\mathbf{p}’$ แล้วท้ายที่สุดเราก็เลื่อนขนาน $\mathbf{p}’$ ออกไปด้วย $\mathbf{p}{-}\mathbf{p}^\ast$ เพื่อให้ผลลัพธ์กลับอยู่ห่างจากระนาบ $\Xi_\mathbf{u}$ เป็นระยะทางเท่าเดิมนั่นเอง

แต่ว่าเรามีวิธีที่เรียบง่ายกว่านั้น และที่เราทำเช่นนี้ได้ก็เพราะว่าควอเทอร์เนียนไม่มีสมบัติสลับที่การคูณ นั่นก็คือเรารู้อยู่เต็มอกว่า การเอาตัวหมุนไปคูณทางด้านขวา $\mathbf{p}(\cos\theta+\mathbf{u}\sin\theta)$ นั้นจะให้ผลลัพธ์เป็นการหมุนทวนเข็มนาฬิกา แต่เรายังมีสังยุคของควอเทอร์เนียนที่มันช่วยให้หมุนของในทิศทางตรงกันข้ามได้ด้วย ดังนั้น $\mathbf{p}(\cos\theta-\mathbf{u}\sin\theta)$ จึงกลายเป็นการหมุนตามเข็มนาฬิกา และนั่นไม่ใช่แค่ความดีงามเพียงอย่างเดียวของสังยุค เพราะเมื่อเราสนใจส่วนจริงในผลลัพธ์การคูณด้วยสังยุค เราจะเห็นว่ามันวิ่งกลับข้างกันกับการคูณด้วยควอเทอร์เนียนต้นฉบับ (ไม่ว่าเราจะคูณจากฝั่งซ้ายหรือขวาก็ตาม)

นั่นหมายความว่าถ้าเราเริ่มคูณจุดข้อมูลของเราทางฝั่งซ้ายด้วยควอเทอร์เนียนต้นฉบับ แล้วคูณฝั่งขวาด้วยควอเทอร์เนียนสังยุค ผลลัพธ์ท้ายสุดจะได้ว่าเราหมุนเป็นมุมสองเท่าจากที่เราต้องการ ในขณะที่ส่วนจริงถูกหักล้างให้กลายเป็นศูนย์นั่นเอง นอกจากนี้การหมุนไปในทิศทางเดียวกันด้วยมุมเท่ากันยังช่วยหักล้างความห่างจากระนาบตั้งฉากอีกด้วย

การหมุนในสามมิติที่กำจัดผลข้างเคียงต่างๆ ออกไปแล้ว

ดังนั้นจึงสรุปได้ว่า เมื่อเราต้องการหมุนจุด $\mathbf{p}$ ใดๆ รอบหน่วยจินตภาพ $\mathbf{u}$ ด้วยมุม $\theta$ เราสามารถใช้คู่ของควอเทอร์เนียนต้นฉบับ-สังยุคมาคูณประกบเพื่อสร้างการหมุนได้ โดยที่ควอเทอร์เนียนแต่ละตัวจะแบ่งความรับผิดชอบมุมไปคนละครึ่ง ดังที่ได้เห็นไปแล้วใน $\eqref{eq:quaternion-conjugation}$ หรือเขียนซ้ำอีกรอบได้ดังนี้

\[\mathbf{p}' = \left( \cos\frac\theta2 + \mathbf{u}\sin\frac\theta2 \right) \mathbf{p} \left( \cos\frac\theta2 - \mathbf{u}\sin\frac\theta2 \right)\]

และนี่ก็น่าจะตอบคำถามเรื่องความบ้าคลั่งทั้งหมดของการหมุนด้วยควอเทอร์เนียนได้แล้ว(มั้ง)