โอเรอรี่เป็นเครื่องมือทางดาราศาสตร์อย่างหนึ่งที่ช่วยให้เรา “เห็นภาพ” และเรียนรู้เกี่ยวกับระบบสุริยะ โดยมันจะจำลองลักษณะต่างๆ ของดวงอาทิตย์ดาวเคราะห์และดาวบริวาร ไม่ว่าจะเป็น ขนาด ตำแหน่ง วงโคจร ไปจนถึงการหมุนรอบตัวเอง พูดง่ายๆ ว่ามันก็คือนาฬิกาดาราศาสตร์แบบหนึ่งนั่นแหล่ะ ซึ่งก็แน่นอนว่าเครื่องมือในลักษณะเช่นนี้ถูกคิดค้นพัฒนาขึ้นมาอย่างยาวนานตามประวัติศาสตร์มนุษยชาติ แต่ว่าหมุดหมายสำคัญของโอเรอรี่ยุคใหม่นี้เริ่มนับที่ปี 1713 เมื่อ George Graham ได้ประดิษฐ์โมเดลระบบสุริยะด้วยกลไกฟันเฟืองที่จำลองการโคจรของดาวเคราะห์ต่างๆ ได้อย่างแม่นยำเพื่อนำไปเสนอต่อเอิร์ลแห่งโอเรอรี่ (จึงเป็นที่มาของชื่อเครื่องมือชิ้นนี้นั่นเอง)

ถึงแม้ทุกวันนี้คอมพิวเตอร์อิเล็กทรอนิกส์จะสามารถคำนวณวัตถุทางดาราศาสตร์ได้อย่างละเอียดแม่นยำ จนเราไม่มีความจำเป็นต้องพึ่งพาโอเรอรี่แบบกลไกฟันเฟืองในงานทางดาราศาสตร์อีกต่อไปแล้ว แต่กลไกฟันเฟืองที่ดูเรียบง่ายแต่ก็ซับซ้อนนี้ก็มีเสน่ห์ชวนหลงไหลอย่างเหลือเชื่อ มันจึงเป็นเรื่องน่ายินดียิ่งนักเมื่อ LEGO ได้นำเสนอโมเดลหมายเลข 42179 ที่จำลองความสัมพันธ์ระหว่างดวงอาทิตย์-โลก-ดวงจันทร์ให้เราได้เล่นสนุกและเรียนรู้กับมัน¹

โมเดลนี้สนใจอะไรบ้าง?

เมื่อเรานึกถึงโมเดลแบบจำลองใดๆ ขึ้นมาซักชิ้นนึง เราคงไม่สามารถถ่ายทอดความสมจริงทุกประการลงมายังโมเดลชิ้นนี้ได้ เช่น ในโมเดลทางดาราศาสตร์โดยทั่วไปก็จะติดข้อจำกัดด้านอัตราส่วนขนาดต่างๆ นั่นคือถ้าเราย่อดวงอาทิตย์ลงมาที่เส้นผ่านศูนย์กลาง 1.4 เมตร (ประมาณเก้าอี้บีนแบคขนาดใหญ่) แล้วโลกจะมีเส้นผ่านศูนย์กลางแค่ 1.3 เซนติเมตร (เมล็ดกาแฟ) เท่านั้น! แถมระยะห่างจากโลกถึงดวงอาทิตย์ก็คือ 150 เมตร (สามสระว่ายน้ำมาตรฐาน) อีกด้วย!! เรียกได้ว่าโมเดลเช่นนี้นอกจากจะนำไปสร้างจริงได้ยากแล้ว ยังทำให้เราไม่สามารถใส่รายละเอียดอื่นๆ ที่น่าสนใจลงไปได้อยู่ดี … (แต่ถ้าใครอยากจะเห็นโมเดลในอัตราส่วนที่ถูกต้องทั้งขนาดและระยะทางเช่นนี้ อาจลองตีตั๋วเครื่องบินไปดูที่ชายหาดเมืองเมลเบิร์นได้)

ดังนั้นมันจึงเป็นเรื่องปรกติที่เรามักจะต้องเสียสละความสมจริงอะไรบางอย่างทิ้งไป เพื่อให้ยังสามารถสร้างโมเดลที่มีความหมายขึ้นมาได้ ตัวอย่างง่ายๆ ที่เราเห็นกันจนชินตาก็คือแผนที่ระบบสุริยะ ที่มักวาดทั้งขนาดและระยะห่างต่างๆ ผิดเพี้ยน (ไปจนถึงการลดทอนความซับซ้อนของวงโคจรที่ควรเป็นวงรีให้เหลือเพียงแค่วงกลม) นั่นเอง

แล้วโมเดล LEGO ชิ้นนี้รักษาความสมจริง/เสียสละอะไรไปบ้าง?

• อัตรตราส่วนขนาดระหว่างโลกกับดวงอาทิตย์นั้นเพื้ยนแน่ๆ (เรื่องระยะห่างนี่ยิ่งไม่ต้องพูดถึง)
• แต่อัตราส่วนขนาดระหว่างโลกกับดวงจันทร์กลับทำได้ดีอย่างไม่น่าเชื่อ ซึ่งก็คือเส้นผ่านศูนย์กลางในโมเดลนี้เท่ากับ 3.9 ซม. กับ 1.1 ซม. ตามลำดับ (รัศมีจริงที่ 6371 กม. กับ 1737 กม.) อย่างไรก็ตาม ระยะห่างระหว่างโลกกับดวงจันทร์ก็ยังไม่ถูกอยู่ดี (ไม่งั้นโมเดลส่วนนี้จะต้องมีระยะห่างถึงสองเมตรครึ่ง)
• แกนเอียงของโลก (ตัวการที่ทำให้เกิดฤดูกาล) จากของจริงที่ 23.44 องศา ถูกนำมาแปลงเป็นโมเดลที่ 22.5 องศา (ซึ่งก็คือ LEGO นำชิ้นส่วนเดิมที่มีอยู่มาใช้งานเลย เพราะว่ามันเป็นชิ้นส่วนพื้นฐานที่เกิดจากการแบ่งมุมฉากออกเป็นสี่ส่วนเท่ากัน)
• ในโมเดลนี้ดวงจันทร์โคจรรอบโลกด้วยระนาบที่สูงเท่าเดิมตลอด นั่นหมายถึงเราจะมีสุริยุ/จันทรุปราคาทุกเดือน แต่ในความเป็นจริงแล้วทั้งสองเหตุการณ์จะเกิดได้ราวๆ หกเดือนครั้งเท่านั้น เพราะระนาบวงโคจรของดวงจันทร์นั้นเอียงเล็กน้อยจนดวงอาทิตย์-โลก-ดวงจันทร์ไม่อยู่ในแนวเส้นตรงเดียวกันพอดีทุกเดือนนั่นเอง (อ่านเพิ่ม: มาคำนวณสุริยุปราคาอย่างง่ายกันเถอะ)
• วงโคจรทุกอย่างในโมเดลนี้เป็นวงกลม แถมดาวแต่ละดวงก็อยู่ ณ จุดศูนย์กลางวงกลมแต่ละวงพอดีอีกด้วย — ในความจริงวงโคจรจะเป็นวงรีที่มีดาวแต่ละดวง ณ จุดโฟกัสจุดหนึ่งของวงรี ถึงแม้ว่าค่าความรีจะน้อยมากจนดูเหมือนว่าวงโคจรจะเป็นวงกลมก็ตามที อนึ่ง นอกจากประเด็นด้านความรีแล้ว คู่โลก-ดวงจันทร์ก็ถือว่ามีขนาดมวลไม่ห่างกันมากนัก จนในความเป็นจริงโลกจะต้องโคจรรอบจุดศูนย์กลางมวลของทั้งคู่ โดยจุดนี้มันจะเหลื่อมออกมาจากจุดศูนย์กลางโลก (จนเกือบจะถึงผิวโลก) อีกด้วย

อย่างไรก็ตาม ส่วนที่น่าจะเป็นหัวใจสำคัญที่สุดในโมเดลแบบโอเรอรี่เช่นนี้ ก็ควรจะต้องเป็นมิติด้านเวลา นั่นคือเราจะสนใจตำแหน่งในวงโคจรและการหมุนรอบตัวเอง ณ เวลาต่างๆ ซึ่งการจะตอบว่า LEGO ชุดนี้ทำได้ดีแค่ไหน ก่อนอื่นจะขอเริ่มจากการย้อนกลับไปทบทวนเรื่องพื้นฐานที่หลายคนมักมองข้ามไปก่อน นั่นก็คือเรื่องง่ายๆ อย่างการนับเวลา

ความยาวของวันเวลา

สำหรับมุนษย์ (ส่วนใหญ่) ที่ออกไปใช้ชีวิตเมื่อพระอาทิตย์ขึ้นและนอนหลับพักผ่อนยามอาทิตย์ตก เราได้กำหนดตกลงกันไว้ว่าหนึ่งรอบของการใช้ชีวิตเช่นนี้คือ “หนึ่งวัน” แนวคิดนี้มีความผูกพันธ์กับดวงอาทิตย์เป็นอย่างมาก พูดโดยคร่าวๆ ก็คือเราจะนับว่าเวลาผ่านไปหนึ่งวันเมื่อเรามองเห็นดวงอาทิตย์เคลื่อนที่วนกลับมาอยู่บนตำแหน่งเดิมบนท้องฟ้าหนึ่งรอบ (แล้วหลังจากนั้นเราจึงแบ่งย่อย 1 วันให้เป็น 24 ชั่วโมง หรือก็คือ 1440 นาที หรือก็คือ 86400 วินาทีตามลำดับ)

จริงอยู่ที่การตีความ “หนึ่งวัน” เช่นนี้มันเป็นเรื่องที่ตรงไปตรงมา แต่สำหรับการคำนวณทางดาราศาสตร์แล้วมันอาจไม่พอ เพราะในบางสถานการณ์นั้นเราไม่ได้ต้องการอ้างอิงดวงอาทิตย์เป็นหลัก เช่น หากเราต้องการถามว่าดาวซานถี่จะวนกลับมาอยู่ ณ ตำแหน่งเดิมบนท้องฟ้าเมื่อสังเกตจากโลกที่เวลาเท่าไหร่ เราจะพบว่ามันไม่ได้ใช้เวลาเท่ากับ 24 ชั่วโมงพอดีอีกแล้ว แต่จะกินเวลาน้อยลงไปประมาณ 3:56 นาที ความแตกต่างเพียงเล็กน้อยนี้ไม่ใช่ความผิดพลาดจากการวัดแต่อย่างใด แต่เป็นเพราะว่านอกจากโลกจะหมุนรอบตัวเองแล้วโลกก็ยังโคจรรอบดวงอาทิตย์อีกด้วย ซึ่งทิศทางการหมุนรอบตัวเองและรอบดวงอาทิตย์นั้นก็คือทิศทางเดียวกัน (ทวนเข็มนาฬิกาเมื่อมองลงมายังทางขั้วโลกเหนือ) นั่นก็คือโลกจะต้องใช้เวลามากกว่าเพื่อนหมุนรอบตัวเองให้หันกลับไปจนถึงดวงอาทิตย์เมื่อเทียบกับหมุนไปหาดาวที่อยู่ไกลมากๆ จนแทบไม่ขยับเขยื้อน

วันสุริยคติและวันดาราคติ ภาพจาก WikiPedia

เราเรียกวันแบบแรก(ที่มนุษย์คุ้นเคย)ที่ดวงอาทิตย์วนกลับมาอยู่ตำแหน่งเดิมว่าวันสุริยคติ (synodic day)² และเรียกวันแบบที่สองที่สนใจดาวฉากหลังแทนว่าวันดาราคติ (sidereal day) … การแบ่งวิธีนับวันออกเป็นสองแบบเช่นนี้ ดูเผินๆ อาจเป็นการเพิ่มความยุ่งยากซับซ้อนไปจนถึงขั้นทำให้งุนงงได้ (ซึ่งก็มีส่วนจริงอยู่บ้าง เช่น โจทย์กลิ้งวงกลมในตำนาน) แต่จริงๆ แล้วความสัมพันธ์ของการนับวันทั้งสองแบบนั้นแสนจะเรียบง่าย นั่นคือ เมื่อโลกโคจรรอบดวงอาทิตย์ครบหนึ่งรอบแล้ว จำนวนวันดาราคติจะมีมากกว่าวันแบบสุริยคติเท่ากับหนึ่งพอดี ไม่ขาด ไม่เกิน

ในกรณีของโลกอาจจะไม่เห็นผลมากเท่าใดนัก (เพราะไม่ว่าเราจะสนใจวันแบบไหน ก็จะเห็นว่าจำนวนรอบมันสูงเกินกว่าสามร้อยรอบ) แต่คาบวงโคจรของดวงจันทร์นั้นน่าสนใจกว่ามากๆ กล่าวคือ ดวงจันทร์ที่โคจรกลับมาอยู่ตำแหน่งเดิมบนท้องฟ้าเมื่อเทียบกับตำแหน่งดวงอาทิตย์ที่ 29.53 วัน (ซึ่งนั่นก็คือนิยามดั้งเดิมของเดือนสำหรับมนุษย์ ที่นับว่าช่วงเวลาตั้งแต่จันทร์เพ็ญถึงจันทร์เพ็ญอีกครั้งนั้นยาวนานหนึ่งเดือน) เราจะเรียกการนับแบบนี้ว่าเดือนจันทรคติ (lunar month) ส่วนอีกทางหนึ่งที่สนใจดวงจันทร์โคจรกลับมาอยู่ตำแหน่งเดิมเทียบกับดาวฉากหลังจะนับได้เพียง 27.32 วัน ซึ่งเราจะเรียกมันว่าเดือนดาราคติ (sidereal month) คราวนี้เราจะเห็นความแตกต่างสำคัญว่าในหนึ่งปีจะมี 12.37 เดือนจันทรคติ หรือก็คือเทียบเท่ากับ 13.37 เดือนดาราคติ

อัตราส่วนเฟือง

อีกเรื่องพื้นฐานที่มองข้ามไม่ได้ก็คืออัตราส่วนเฟือง ซึ่งจะช่วยให้เราสร้างโมเดลนี้ได้อย่างถูกต้องและใช้ชิ้นส่วนอย่างสมเหตุสมผล เพื่อความเรียบง่าย ในตอนนี้เราจะสนใจโมเดลที่มีเพียงแค่ดวงอาทิตย์เพียงอย่างเดียวไปก่อน โดยถือว่าดวงอาทิตย์หมุนรอบตัวเองหนึ่งรอบด้วยระยะเวลา 27 วัน (ดวงอาทิตย์จริงๆ เป็นดาวแก๊ส จึงทำให้คาบการหมุนรอบตัวเองตามละติจูดต่างๆ ไม่คงที่ โดยอาจกินระยะเวลาได้ตั้งแต่ 25~35 วัน)

สมมติเราต้องการสร้างโมเดลที่มีที่จับมือหมุน (hand crank) เพื่อควบคุมการหมุนของดวงอาทิตย์ โดยถือว่าการหมุนมือหนึ่งรอบเท่ากับระยะเวลาหนึ่งวัน วิธีตรงไปตรงมาที่สุดสำหรับมือใหม่ด้านกลไก ก็คงหนีไม่พ้นการใช้เฟืองเพียงแค่สองเฟืองที่มีจำนวนฟันแตกต่างกันมากๆ เช่นนี้

เฟืองเล็ก (12-ฟัน) และเฟืองใหญ่ (ที่ควรจะมี 324-ฟัน แต่มีไม่ถึงเพราะเฟืองใหญ่สุดคือ 60-ฟัน)

จะเห็นว่า การหมุนเฟืองเล็กหนึ่งรอบนั้นเทียบเท่ากับการเลื่อนฟันเฟืองไป 12 ฟัน ดังนั้นมันจะส่งผลต่อให้ฟันเฟืองใหญ่ (ที่มีทั้งหมด 324-ฟัน) เลื่อนตามเท่ากับ 12 ฟันเช่นกัน นั่นก็คือการหมุนเฟืองเล็กหนึ่งรอบจะทำให้เฟืองใหญ่หมุน 12/324 = 1/27 รอบนั่นเอง

เราจะเรียกอัตราส่วนจำนวนรอบของเฟืองต้นทางไปยังเฟืองปลายทางว่า อัตราส่วนเฟือง และมันก็คำนวนได้ง่ายๆ จากการนำจำนวนฟันของเฟืองต้นทางมาหารเฟืองปลายทางนั่นเอง (ส่วนถ้าอยากรู้ว่าต้องหมุนเฟืองต้นทางกี่รอบให้เฟืองปลายทางหมุนได้หนึ่งรอบ ก็ให้เอาหนึ่งไปหารค่าอัตราส่วนเฟืองอีกที)

แต่การออกแบบเช่นนี้ก็คงไม่เหมาะสมเท่าใดนัก ทั้งขนาดของเฟืองที่ใหญ่เกินไปจนกินเนื้อที่เกินจำเป็น ยังไม่นับค่าใช้จ่ายของการสร้างเฟืองขนาดไม่มาตรฐานแทนที่จะใช้เฟืองที่มีอยู่แล้ว เราจึงอยากจะลดขนาดของกลไกเราลงมาโดยใช้เฟืองหลายๆ อันมาทำงานร่วมกันแทน โดยข้อสังเกตสำคัญก็คือเฟืองที่เชื่อมด้วยแกน (axle) เดียวกันจะหมุนได้จำนวนรอบเท่ากันเสมอ (อย่างน้อยก็ในโลกอุดมคติที่เราไม่คำนึงถึงความทนทานวัสดุ) ดังนั้นเราอาจออกแบบเฟืองใหม่ได้ดังนี้

ตัวอย่างชุดเฟืองที่แต่ละคู่ย่อยมีอัตราเฟือง 1/3 และมีอัตราเฟืองทั้งระบบเป็น 1/27

กลไกชุดใหม่นี้นอกจากจะกินพื้นที่น้อยลงอย่างมาก มันยังใช้เฟืองมาตรฐานเพียงแค่สองแบบ คือ 12-ฟัน กับ 36-ฟัน อีกด้วย ซึ่งถือว่าเรียบง่ายคู่ควรกับโลกวิศวกรรมมากๆ แต่คำถามที่สำคัญก็คือ แล้วการหมุนมือหนึ่งรอบมันจะส่งผลให้ดวงอาทิตย์จำลองหมุนได้กี่รอบหล่ะ? (พูดนั่นก็คือ มันจะยังทำงานได้ถูกต้องอยู่มั้ย)

สังเกตว่าคู่เฟืองชุดแรกนั้นมีอัตราเฟืองที่ 1/3 (นั่นก็คือเมื่อหมุนเฟือง 12-ฟันไปหนึ่งรอบ จะหมุนเฟือง 36-ฟันได้หนึ่งในสามรอบ) ทีนี้เมื่อเราจะพิจารณาเฟืองคู่ถัดมา สังเกตว่าเฟือง 32-ฟันจากชุดแรกนั้นอยู่บนแกนเดียวกันกับเฟือง 12-ฟันของชุดที่สอง ดังนั้นเฟือง 12-ฟันนี้จึงจะหมุนได้แค่หนึ่งในสามและส่งผลให้เฟือง 32-ฟันของชุดที่สองหมุนแค่หนึ่งในเก้า … ดังนั้นเมื่อคิดทั้งหมด เราจะได้ว่าอัตราส่วนเฟืองจากต้นทางมือหมุนไปจนถึงปลายทางดวงอาทิตย์ คือ (1/3)(1/3)(1/3) = 1/27 ตามที่เราต้องการนั่นเอง

สรุปได้อย่างเรียบง่ายว่า อัตราส่วนเฟืองในภาพรวมนั้นก็คือผลคูณของอัตราส่วนเฟืองย่อยๆ แค่นั้นแหละ (เพื่อความเรียบง่าย จะขอละเครื่องหมายแสดงทิศทางการหมุนทิ้งไป)

อนึ่ง ภาพประกอบในหัวข้อนี้สร้างจากเว็บ Technic Brick Power ที่สามารถนำเฟือง LEGO มาประกบต่อกันเพื่อจำลองการเคลื่อนไหวและวัดอัตราส่วนเฟืองได้

คำนวณเฟืองโมเดล LEGO

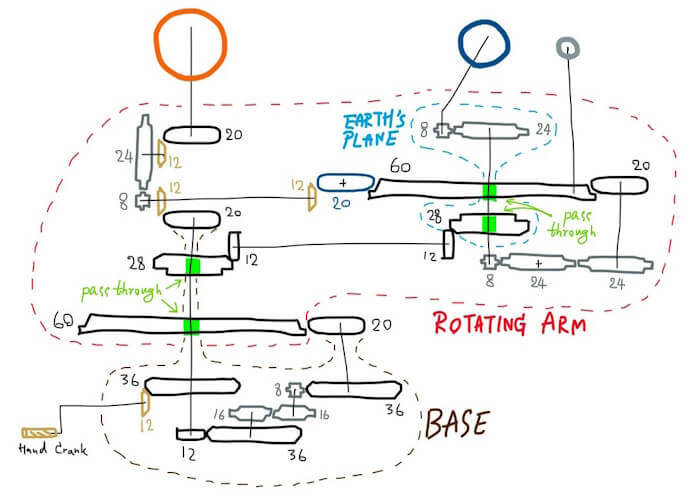
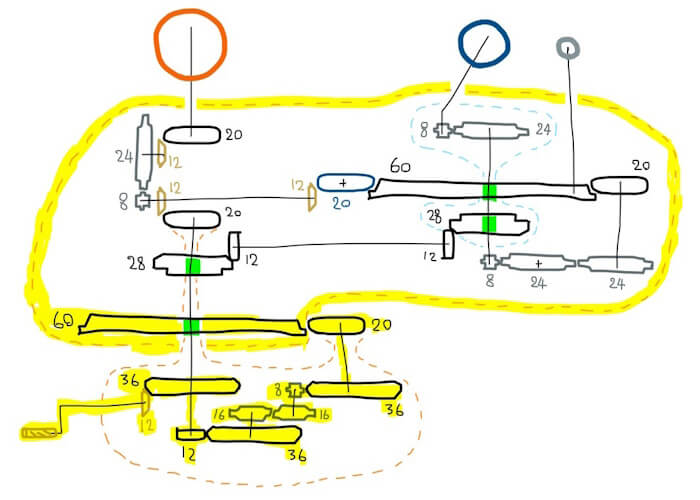
ถึงตอนนี้เราก็สามารถคำนวณได้เสียทีว่า โมเดล LEGO ชุดนี้ถ่ายทอดมิติเวลามาได้แม่นยำแค่ไหน โดยแผนภาพระบบเฟืองของโมเดลเป็นดังนี้

ภาพรวมระบบเฟืองของ LEGO ชุด 42179

ซึ่งทำให้เราคำนวณอัตราส่วนเฟืองออกมาได้ว่า

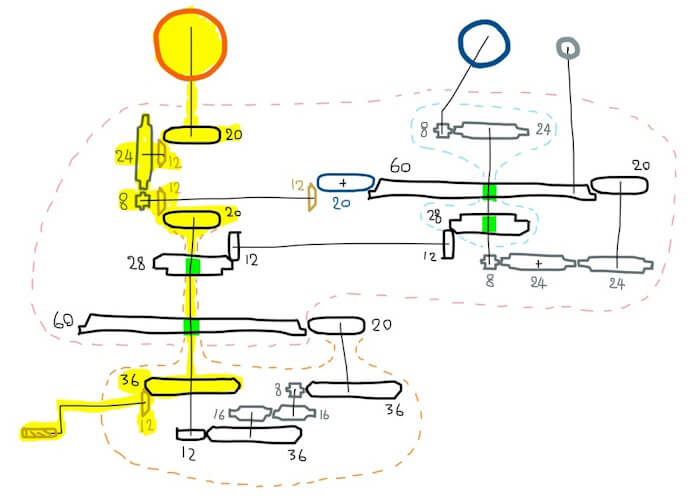
ดวงอาทิตย์หมุนรอบตัวเอง 1/9

(1/3)(5/3)(1/3)(3/5) = 1/9

ดวงอาทิตย์นี่ดูง่ายที่สุดเพราะแค่ต่อจากฐานขึ้นไปตรงๆ จะมีส่วนที่ชวนสงสัยก็ตรงการแปลง 20-ฟัน ไป 12-ฟัน แต่แล้วก็แปลง 12-ฟัน กลับมา 20-ฟัน อยู่ดี (ซึ่งก็คือจะได้อัตราส่วนเฟืองเป็นหนึ่ง หรือก็คือไม่ทำอะไรเลย) แต่พอดูดีๆ ก็เข้าใจได้ว่าการเพิ่มเฟืองเช่นนี้ก็เพื่อหลบคู่เฟือง 8/24 ออกมาด้านนอกเพราะพื้นที่ไม่พอ

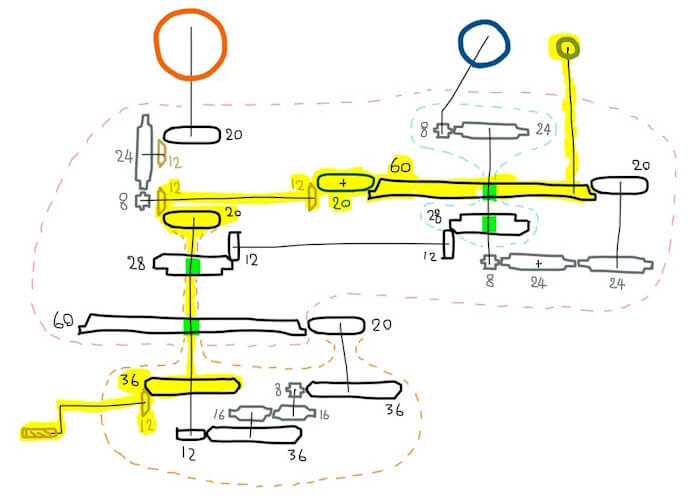
ดวงจันทร์โคจรรอบโลก 1/9

(1/3)(5/3)(3/5)(1/3) = 1/9

กลไกถัดมาที่จะเห็นได้คือดวงจันทร์โคจรรอบโลกแบบเดือนดาราคติ ซึ่งมีอัตราส่วนเฟืองที่ 1/9 เช่นเดียวกับดวงอาทิตย์หมุนรอบตัวเอง แต่แทนที่ LEGO จะออกแบบอัตราเฟือง 1/9 ตรงๆ จากฐานแล้วส่งมาให้ทั้งดวงอาทิตย์และดวงจันทร์ กลับเลือกที่จะส่งมาแค่ 1/3 แล้วให้คู่เฟือง 20/60 ที่ดวงจันทร์รับจบ ซึ่งก็ถือว่าเป็นสไตล์การออกแบบที่น่าสนใจ เพราะเฟือง 60-ฟัน นั้นมีขนาดที่ใหญ่มาก (ใหญ่ที่สุดเท่าที่ LEGO ผลิต??) จนสามารถเอาเสาดวงจันทร์ไปปักบนตัวเฟืองได้เลย

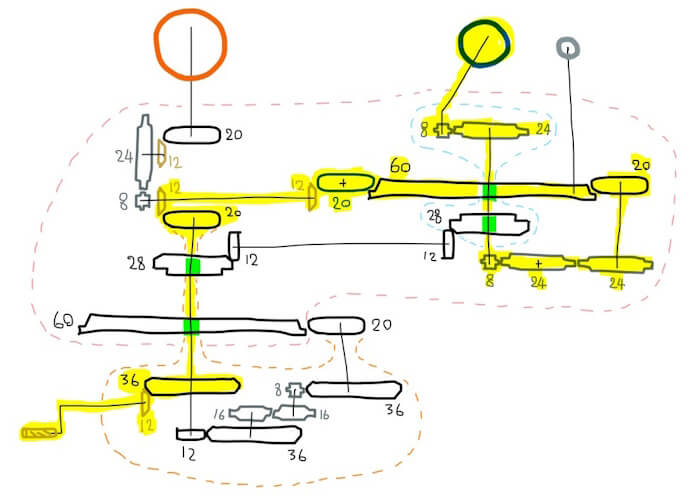
โลกหมุนรอบตัวเอง 3/1

(1/3)(5/3)(3/5)(1/3)(3/1)(1/1)(3/1)(3/1) = 3/1

โลกหมุนรอบตัวเองแบบวันดาราคตินั้น เอาผลลัพธ์จากดวงจันทร์มาคำนวณต่อได้เลย โดยมันเป็นอัตราส่วนเฟืองอันเดียวในโมเดลนี้ที่มีค่าเกินหนึ่ง

โลกโคจรรอบดวงอาทิตย์ 2/243

(1/3)(1/3)(1/1)(2/9)(1/3) = 2/243

อัตราส่วนเฟืองที่น่ามหัศจรรย์ที่สุดก็คงเป็นโลกโคจรรอบดวงอาทิตย์ ซึ่งตอนแรกนึกว่าเค้าจะลดความยุ่งยากของโมเดลให้เหลือแค่ 360 วันต่อปีด้วยซ้ำ (เพราะเลขนี้สามารถแยกตัวประกอบได้เยอะมาก) แต่ LEGO กลับเลือกใช้อัตราส่วนที่สร้างได้จากเลขง่ายๆ เพียงแค่สองตัว คือ 2/3⁵ = 2/243 ซึ่งดูเผินๆ อาจจะคิดว่าได้ค่าประหลาดที่น่าจะเพี้ยนหรือเปล่า แต่เมื่อคำนวณย้อนกลับไปแล้วจะได้ว่ามันคือ 364.5 วัน ซึ่งใกล้เคียงความจริงยิ่งกว่าการลดทอนไปเป็น 360 วันเสียอีก!

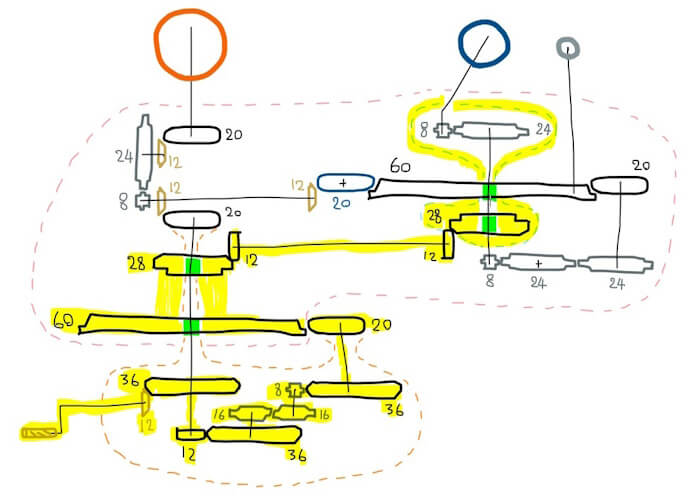
แก้ระนาบแกนโลกเอียงให้คงที่

แต่ส่วนที่น่าสนใจในระบบกลไกเฟืองที่สุดก็คงหนีไม่พ้นตรงการแก้ระนาบโลก เนื่องจากว่าแกนเอียงของโลกนั้นจะต้องเอียงชี้ไปทางทิศเดิมเสมอ (อย่างน้อยก็ในระดับหลายร้อยปี) จึงต้องมีเฟืองอีกชุดมาคอยหมุนในทางตรงข้ามเพื่อแก้ระนาบแกนเอียงโลกด้วย ซึ่งก็คือชุดเฟืองคู่ตรงข้าม 28/12 และ 12/28 นั่นเอง

สรุปผลการคำนวณ

	อัตราส่วนเฟือง	เทียบเป็นเวลาต่อรอบ	ข้อมูลจริง (วันดาราคติ)
มือหมุน	1	3	-
ดวงอาทิตย์หมุนรอบตัวเอง	1/9	27	25~35
ดวงจันทร์โคจรรอบโลก (เดือนดาราคติ)	1/9	27	27.39
โลกหมุนรอบตัวเอง (วันดาราคติ)	3/1	1	1
โลกโคจรรอบดวงอาทิตย์	2/243	364.5	366.25

นับว่าโมเดลนี้ทำได้ดีใกล้เคียงกับข้อมูลจริงมากๆ เลยทีเดียว!

มาลองหมุนโมเดล LEGO กันเถอะ

แต่เรื่องแปลกก็คือเมื่อเราจับมือหมุนในโมเดลหมุนเล่นอย่างจริงจังเป็นจำนวน 121.5 รอบ (ตามที่คำนวณได้จากอัตราส่วนเฟือง) จะพบว่าดวงจันทร์นั้นไม่ได้โคจร 13.5 รอบเดือนดาราคติตามที่คำนวณไว้ แต่จะนับได้ 14 รอบกว่าๆ แทน… ต้องมีอะไรผิดพลาดตรงไหนแล้วหล่ะ

กลายเป็นว่าสิ่งที่เราลืมคิดไปก็คือ ส่วนแขนทั้งหมดของโมเดลนั้นมันหมุนไปทั้งอันด้วย! นั่นหมายความว่าเมื่อแขนที่ถือโลกและดวงจันทร์หมุนจนครบรอบปีแล้ว เราก็ควรจะต้องนับได้เพิ่มอีกหนึ่งรอบเดือนดาราคติด้วย กลายเป็น 14.5 รอบนั่นเอง

ผิดอยู่ดี!! เพราะถ้าเราตั้งใจทดลอง-วัดค่า-บันทึกผลจริงๆ จะนับได้ว่าดวงจันทร์โคจรเพียงแค่ 14⅙ รอบเดือนดาราคติเท่านั้น

แล้วความผิดพลาดมาจากไหน?

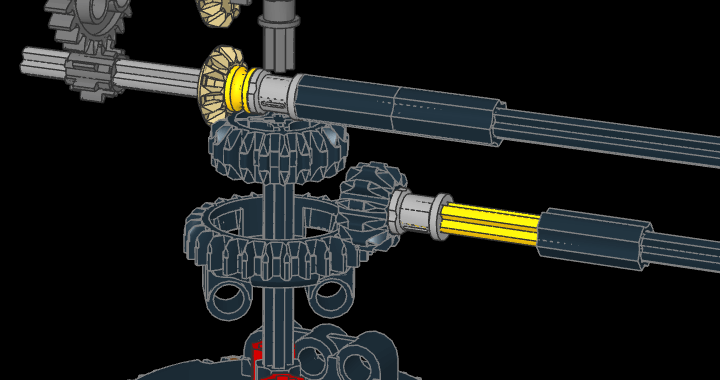
อันที่จริงแล้วส่วนแขนของโมเดลทั้งอันนั้นคือเฟืองเชิงอนุพันธ์ (differential gear)³ ที่มันจะช่วยเพิ่ม/ลดจำนวนรอบได้เฟืองได้อีกหนึ่ง ซึ่งเราสามารถนำคำอธิบายในทำนองเดียวกับวันสุริยคติ/ดาราคติมาช่วยทำความเข้าใจได้เลยนั่นเอง

เฟืองเชิงอนุพันธ์: เฟืองเหลือง 12-ฟัน ต้องหมุนวนรอบ เฟืองดำ 20-ฟัน ตัวล่างด้วย (เสียดายที่โปรแกรมคำนวณไม่สามารถจำลองเฟืองเชิงอนุพันธ์ที่ซับซ้อนได้)

หัวใจหลักสำคัญคือเราต้องเลือกกรอบอ้างอิงให้ถูก เช่นในกรณีนี้ก็คือเราจะเริ่มดูจากเฟืองสีดำ 20-ฟัน ที่ต่อออกมาจากฐานโมเดล เพราะว่าอัตราส่วนเฟืองจากมือหมุนมาถึงตรงนี้คือ 1/3 นั่นคือเมื่อเราหมุนมือ 121.5 รอบ เฟืองตัวนี้จะถูกหมุน 40.5 รอบทวนเข็มนาฬิกา แต่เพราะว่าแขนของโมเดลก็จะถูกหมุนไปหนึ่งรอบทวนเข็มนาฬิกาด้วย ดังนั้นจริงๆ แล้วเฟืองสีดำตัวนี้จะหมุนเพียงแค่ 39.5 รอบเท่านั้น เมื่อเปลี่ยนไปมองว่าแขนของโมเดลเป็นกรอบอ้างอิง

พูดอีกอย่างก็คือเราใช้อัตราเฟืองที่ 1/3 ไม่ได้แล้ว (ซึ่งอัตรานี้ไม่ได้ผิดอะไรหากเราจะเอาไปใช้ต่อในจุดอื่นที่อ้างอิงกับฐานได้) แต่เราต้องเปลี่ยนไปใช้ 1/3 - 2/243 = 79/243 ต่างหาก ถึงจะทำให้การคำนวณที่เหลือบนแขนโมเดลที่หมุนตามไปด้วยนั้นไม่เพี้ยนตาม

นั่นคือเราได้ว่า อัตราส่วนเฟืองเชิงอนุพันธ์ = (อัตราส่วนเฟืองจากฐาน) ± (อัตราส่วนเฟืองแท่นหมุน) โดยเครื่องหมายความเป็นบวกหรือลบนั้นขึ้นอยู่กับว่าเฟืองทั้งสองนั้นหมุนสวนทิศทางกันหรือไม่

ดังนั้นเราจะคำนวณอัตราเฟืองสำหรับดวงจันทร์ใหม่ได้เป็น (79/243)(5/3)(3/5)(1/3) = 79/729 นั่นหมายความว่าเมื่อเราหมุนมือหมุน 121.5 รอบ เราจะได้ว่าดวงจันทร์โคจรเป็น 13⅙ รอบเดือนจันทรคติในกรอบอ้างอิงแขนโมเดล หรือก็คือ 14⅙ รอบเดือนดาราคติในกรอบอ้างอิงฐานโมเดล ซึ่งก็คือถูกต้องตรงตามที่เราสังเกตการณ์นั่นเอง!

แน่นอนว่าดวงอาทิตย์และโลกในโมเดลนี้ก็ได้รับผลกระทบแบบเดียวกัน เพียงแต่ว่าดวงอาทิตย์อาจจะเห็นยากหน่อยเพราะไม่มีจุดสังเกตชัดเจน (แต่ก็จะได้ค่าอัตราส่วนเฟืองเท่ากับกรณีดวงจันทร์อยู่ดีนะ เพราะเฟืองที่เหลือนั้นมีอัตราส่วนเฟืองในทำนองเดียวกันหมดเลย)

ส่วนโลกนั้นจะเจ้าปัญหาหน่อย เพราะว่าตอนจบมันจะไปอยู่บนเฟืองอนุพันธ์อีกชุดหนึ่ง (ระนาบแก้แกนเอียงโลก) ซึ่งก็คือ เราจะคำนวณอัตราเฟืองไปจนถึงเฟืองสี่ตาสีเทาใต้โลกก่อน ซึ่งจะได้ (79/729)(3/1)(3/1) = 79/81 เนื่องจากว่าเฟืองนี้หมุนตามเข็มนาฬิกา และระนาบโลกก็หมุนตามเข็มนาฬิกาด้วย เพราะฉะนั้นอัตราเฟืองชิ้นนี้จริงๆ ควรเป็น 79/81 - 2/243 = 235/243 เมื่อให้ระนาบโลกเป็นกรอบอ้างอิง และคิดอัตราเฟืองต่อจนถึงปลายยอดที่โลกได้ว่าเท่ากับ (235/243)(3/1) = 235/81 = 3 - 8/81

โชคดีที่ระนาบโลกชิ้นนี้จัดกรอบอ้างอิงตัวเองให้ขนานไปกับฐานโมเดลอยู่แล้ว เราจึงคำนวณจำนวนวันดาราคติได้อย่างตรงไปตรงมาเลย นั่นคือเมื่อหมุนมือหมุน 121.5 รอบ โลกจะหมุนรอบตัวเองเป็นจำนวน 352.5 วันดาราคตินั่นเอง

สรุปผลการทดลองและการคำนวณใหม่

	อัตราส่วนเฟือง	เทียบเป็นเวลาต่อรอบ	ข้อมูลจริง (วันดาราคติ)
มือหมุน	1	2.90123	-
ดวงอาทิตย์หมุนรอบตัวเอง	79/729	26.7721	25~35
ดวงจันทร์โคจรรอบโลก (เดือนดาราคติ)	79/729	26.7721	27.39
โลกหมุนรอบตัวเอง (วันดาราคติ)	235/81	1	1
โลกโคจรรอบดวงอาทิตย์	2/243	352.5	366.25

กลายเป็นว่าโมเดลนี้จำลองมิติด้านเวลาได้แย่ลงกว่าเดิมโขเลย หึมม น่าเสียดายที่ตกม้าตายตอนจบจริงๆ 😂