This summer, I came across a cool programming game called ABI-DOS, which is inspired by Zachtronics. It includes a neat little math problem: given a stream of data (as a string of text), determine if a single letter dominates the entire dataset?

Disclaimer: I received the game for free from the developer, Fernando SM, to provide feedback during the beta-testing period.

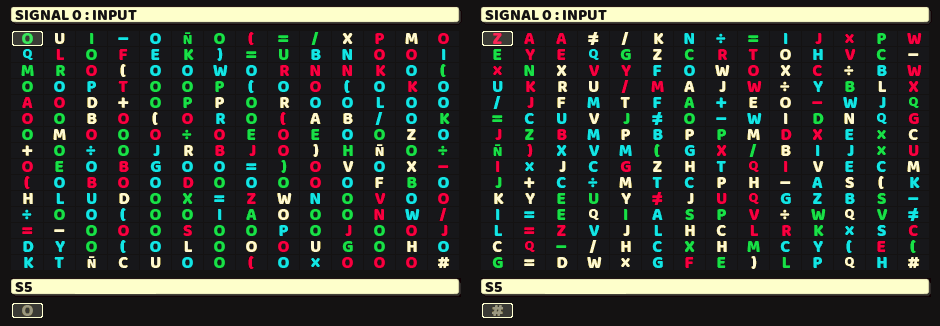
Example test cases of the problem:
(left) the letter O dominates, (right) nothing dominates (output as hashtag)

The problem seems pretty straightforward. Even a 5-year-old could suggest a simple plan: scan through the entire text, count how many times each letter appears, and then check if any letter shows up more than 50% of the time.

Sounds like a good plan, right? And conceptually, it works pretty well for us humans. But it raises some interesting questions: What if the data stream is infinite? Can we sample just a portion of it? How many characters should we sample? And so on.

Besides, counting all those letters by hand would get tedious fast real fast, to be honest. So why not automate it (whether in this fictional machine or one IRL)?

But first, we need to understand how the machine operates. What are its limitations? Can we even implement the above idea on this machine? After all, Knuth once said “Premature optimization is the root of all evil.” If we don’t know what our machine can do, then we’re prone to invoke the devil, right?

Quick reference to ABI-DOS

ABI-DOS is a fictional machine that resembles circuit-like structure.¹ It operates with 3 main components:

1. UBITs: Movable blocks of data containing a numerical value and a color.
2. Icons: Stationary blocks on the circuit board that manipulate UBITs and other icons.
3. Wires: Pathways for UBITs to move along, also serving as hosts for icons.

The interaction between those components is straightforward:

• When a UBIT completely touches an icon, it activates the icon’s function. There are a wild range of functions to choose from: duplicating a UBIT, setting its value, doing some math, etc.
• When two UBITs collide, they merge into one UBIT, with their numerical values added together (and colors blended together).

The workflow is simple. Fire UBITs from input-ports — special icons that emit UBITs with values from the data stream. Perform some computations along the way. Finally, route the resulting UBITs to the correct output-ports.

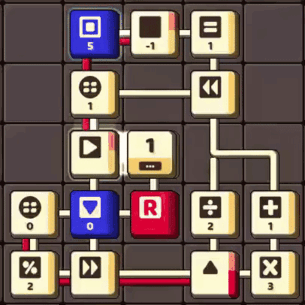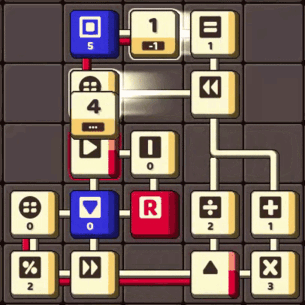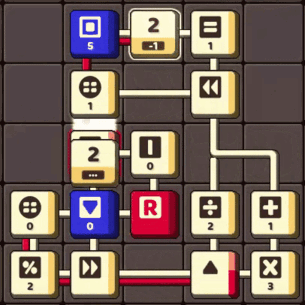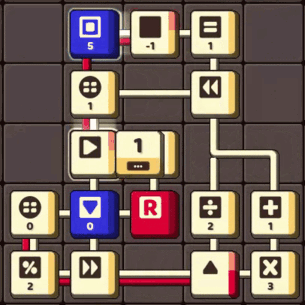
This circuit rounds up odd integers to the nearest even integers

The example circuit fires a UBIT from Port 0, duplicates it into two branches, finds the modulo in one branch, and then merges them back into a single UBIT. Finally, it sends the result UBIT through Port 5, but not before activating an input icon to prompt Port 0 to fire the next UBIT.

There’s also control flow functionality, which operates through 2 sets of icons: sensors and conveyors. Sensors test if a UBIT meets a specific condition and send a true/false trigger to conveyors, which reroute the UBITs accordingly. These components are connected by special red/blue wires that send trigger signals instantly, but do not allow UBITs to traverses.

This circuit computes the length of a given number in Collatz conjecture.

There are also more powerful icons that are useful for solving this problem, such as:

• Obstructors: Hold a UBIT in place for a specified number of cycles, or until receiving a true trigger.
• Writers: Overwritten a value of another icon with a numerical value from a UBIT that activates them.
• Pseudo Ports: Emit a blank UBIT when receiving a true trigger.

While these icons can be quite powerful, the main limitation might be the size of the board. In most levels, the grid is around 8x8 tiles. For this level, it’s a bit more generous with 8x11 tiles.

With this understanding, we’re now ready to tackle the problem. Let’s review our problem statement again.

Detailed problem statement

You are given a stream of data in the form of a text string with a length of approximately $n\approx1000$ characters. Your task is to determine if a single letter dominates the entire text. Importantly, you cannot look back at previous characters as you process the data stream.

For a letter to be considered “dominating”, it must appear more than 50% of the time (in the real game, the dominant letter’s appearance will be slightly exceed 50% to allows probabilistic approaches).

The text will contain around 40 different letters, and the sequence of characters is already shuffled. The text will follows one of two distributions:

• Uniformly: All letters appear roughly equally, meaning each character has probability of $q\approx1/40$ of appearing.
• Anomaly: One letter appears significantly more frequently than the others, with $p\approx1/2$ (the rest are still distributed uniformly, $q’\approx1/80$).

If one letter dominates the dataset, output that letter. Otherwise, output a hashtag (#) to indicate a negative result. The hashtag will only appear once as the last character of the data stream.

A 1-memory algorithm

Given that there are 40 different letters but only two times the space on the machine, it’s improbable to track the occurrence of all letters. Implementing one “virtual memory slot” required at least 1 conveyor and 1 obstructor, not to mention the main logic for rerouting UBITs into the correct slot. So, we need to find a solution that doesn’t rely on memorizing all the letters.

One approach is to track just one letter at a time. For example, we can use the first character as a “pivot” and also initialize a counter to zero. Then, as we read through the entire text (which also includes the first pivot character), we compare each character to the pivot. If a character matches the pivot, we increase the counter by one; if it doesn’t, we decrease the counter by one.

If the pivot letter truly dominates the dataset, the counter will be greater than zero at the end, even though it might dip below zero along the way. (Pretty much life in general, huh?)

To illustrate this, consider a a grid-walking analogy: start at the top-left corner of the grid. Walk to the right if a character matches the pivot, and walk down if it doesn’t. Thus, the grid dimension are $W{\times}H$, where $W$ represents the occurrences of the pivot, and $H$ represents the occurrences of the others. If the pivot dominates, you’ll end up above the diagonal line after walking $n$ steps.

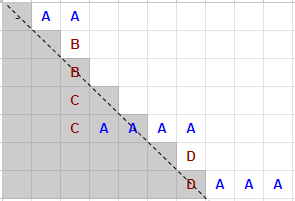
Path for a string “AABB CCAA AADD AAA#”

It’s also true the other way around: when the pivot does not dominate the entire dataset, the counter will eventually drop below zero, in other words, under the diagonal line.

But this only works if we consider the first character as a pivot. What if the dominating letter isn’t the first character we encounter? We need a way to change the pivot to a later character in the stream.

And what is a better way to do this than by changing the pivot when the counter hits zero?

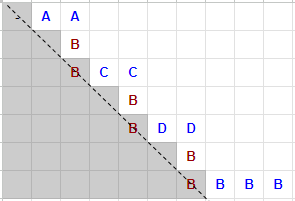
Path with changeable pivot for a string “AABB CCBB DDBB BBB#”

With this framework, there are two key questions we need to address:

1. If there’s a dominating letter, will this letter still be above the diagonal line at the end?
2. If there’s no dominating letter, how far can non-dominating letters raise above the diagonal line?

At first glance, the first question seems to be an issue since the actual dominating letter might be used to walk down the grid (when non-dominating letters are pivots). However, this isn’t actually an issue because the letter already dominates the dataset. At most, the dominating letter will cancel out with non-dominating letters, leaving some portion of the dominating letter behind. Which guarantees that the dominating letter will still be above the line at the end.

To be more precise, the lower bound for the counter of the dominating letter will never be less than $(2p{-}1)n$ characters.

The second question is straightforward. Since letters are uniformly distributed, there will be around $qn\approx25$ characters for each letter.

So we should assume that, when a letter dominates the dataset, it doesn’t just appear exactly 50% of the time, but slightly more by this margin. This leads us to the following algorithm:

1. Initialize a counter to zero, and set the pivot to an empty letter.
2. Read the current character from the input.
3. If the current character is a hashtag (end-of-file), skip to step 7.
4. If the counter is zero, update the pivot to the current character.
5. Increment the counter if the current character matches the pivot; otherwise, decrement it.
6. Loop back to step 2.
7. If the counter is not less than 25, output the pivot; otherwise, output a hashtag.

We can optimize this further. Notice that only in the case of a dominating letter, the counter can exceed 25. So we might “short-circuit” the algorithm by returning the pivot immediately when the counter surpasses this threshold.

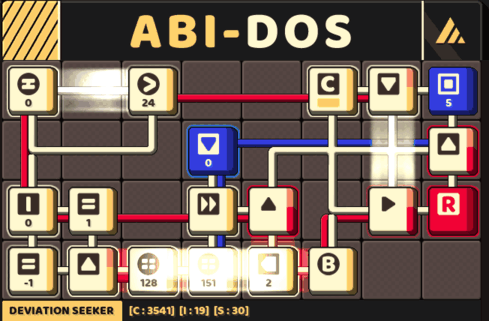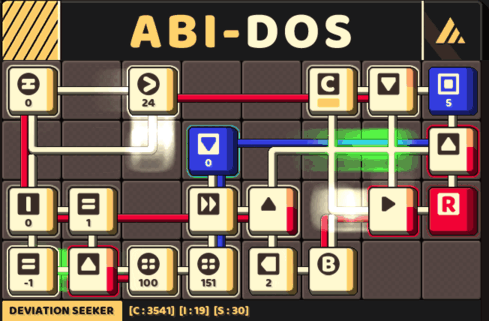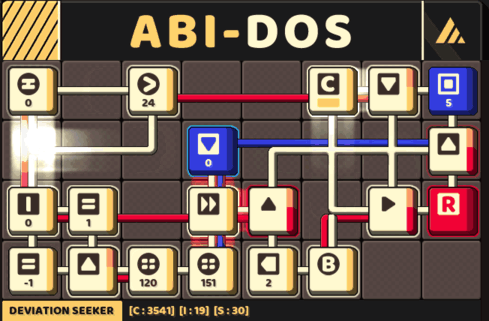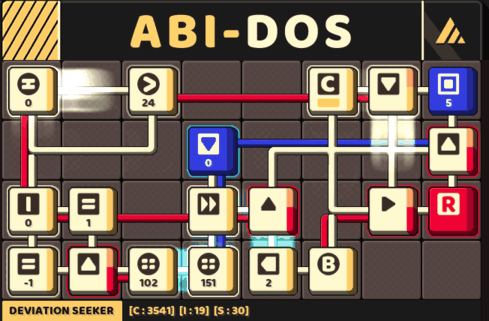
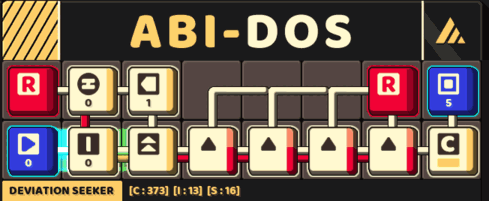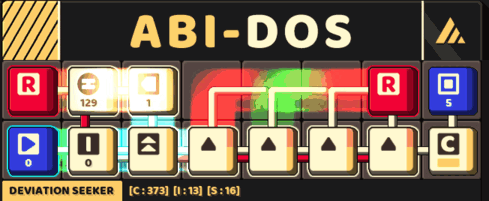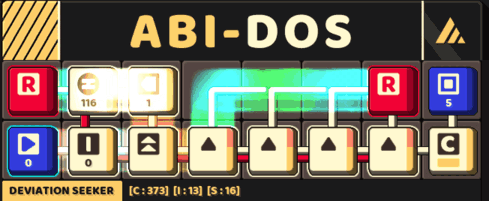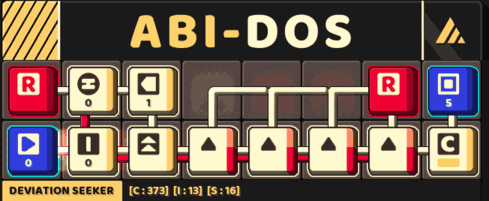
A circuit that track a pair of memory: a pivot and its counter

This implementation would pass all test cases in this game.

A memoryless algorithm (sort of)

The previous circuit works but isn’t fully optimized. Non-dominating letters are very unlikely to increment their counter to 10, let alone 25. Therefore, we can lower this threshold to speed up the algorithm.

Nonetheless, the overall structure of the circuit remains bulky and slow. It requires two loops, each of length 6, for tracking the current pivot and its corresponding counter. If we wish to make the circuit smaller, we need to minimize the space taken by these virtual memory slots—or ideally, eliminate them entirely.

We need to tackle the problem from a different point of view. Let’s re-examine the dataset. Observed that when a letter is dominating, many of its occurrences appear consecutively.

This might seem counterintuitive at first. Even with $p>1/2$, the probability of a $k$-consecutive letter ($k$ characters which all of them are the dominating letter) is only $p^k$. For instance, the probability for a 5-consecutive letter is only 3.1%.

It’ll be hopeless if we only relying on the first $k$ characters. However, since we can continue reading the input until end-of-file, the likelihood of encountering a $k$-consecutive letter is much more higher.

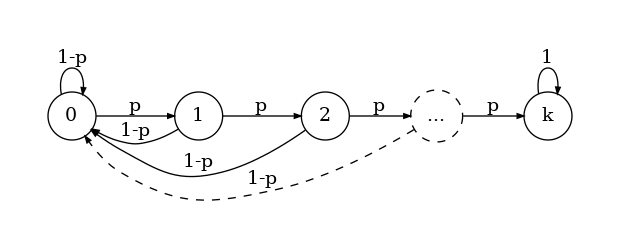
To model this, we can use a Markov chain with $k{+}1$ states. The state transitions indicate the current character matches the dominating letter. Each state, except the final one, has a probability of $p$ of transitioning to the next state, and a probability $1{-}p$ of reverting to state zero. The final state, which indicates that we have successfully found a $k$-consecutive letter, only transitioning to itself.

Markov chain for seeking a $k$-consecutive letter

In other words, we derive a stochastic matrix:

\[\mathbf{M} = \begin{bmatrix} 1{-}p & p & 0 & \cdots & 0 & 0 \\ 1{-}p & 0 & p & & 0 & 0 \\ \vdots & \vdots & & \ddots & & \vdots \\ 1{-}p & 0 & 0 & & p & 0 \\ 1{-}p & 0 & 0 & \cdots & 0 & p \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix}\]

We start with an initial vector, $\vec{v}_0=[1,0,\dots,0]$, which indicate that we start with a 0-consecutive letter. Walking the chain once, (i.e., testing one character if it is the dominating character) can be expressed as

\[\vec{v}_1 = \vec{v}_0 \mathbf{M}.\]

To walk $t$ steps in the chain, we compute

\[\vec{v}_t = \vec{v}_0 \mathbf{M}^t\]

The last entry of $\vec{v}_t$ gives the probability of finding a $k$-consecutive letter. For $k=5$, testing $t=300$ characters gives us 99% confident that we will find a dominating letter if it exists.

On the other hand, we can use the same technique to analyse the case of where there is no dominating letters. At $t=300$, the chance that a non-dominating letter appears consecutively 5 times is 0.00028%. Actually, we can read the entire input ($t=n\approx1000$) and the probability of a false-positive is still 0.00094%. (Also, when the machine runs out of input stream, it will repeat the last entry onward.)

A small circuit that look for a 5-consecutive letter

Thus, the obtain a more streamlined version of the circuit with this approach.

An $m$-memory algorithm

Optimizing for space often means sacrificing speed, a well-known concept in algorithm design called the space–time tradeoff. To achieve the speed aspect, we need to approach the problem from a different angle, again.

Recall our initial algorithm, which use the first character as a pivot and checked if the counter is greater than $n/2$. This approach works only if the dominating letter happens to be the first character, but it fails if the dominating letter appears later in the data stream.

To improve this, we may use two pivots instead: one for the first character and another for the second. This design is more robust, as it can handle cases where the dominating letter is the second character. Yet, it still fails in the same fashion: when the dominating letter appears from the third position onward.

So we can play this cat-and-mouse game, bumping up more pivots to make sure we catch the dominating letter (if there is one). The question is, how many pivots are enough?

The answer is is surprisingly simple. Given that the dominating letter has a probability of $p\approx1/2$ of appearing, using $m$ memory slots ensures that the dominating letter will appear with a probability of $1{-}(1{-}p)^m$. With as few as $m=7$ pivots, we can achieve a 99% confidence level in detecting the dominating letter, thereby avoiding a false-negative result.

With this insight, we can refine our circuit to confidently find the pivot, if one exists. However, since we also aim for a faster algorithm, we need to sample only a subset of the data. How large should the sample be in order to distinguish between dominating and non-dominating cases?

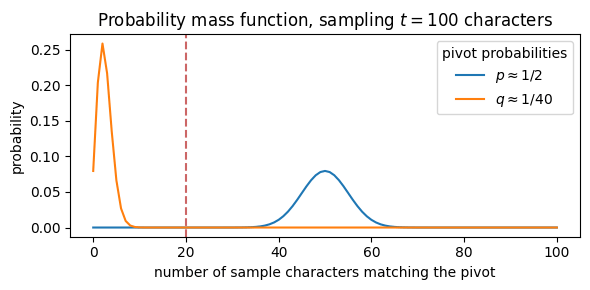
Suppose we sample $t$ characters to test against each pivot. The probability of observing exactly $k$ characters matching the pivot can be described by the binomial distribution:

\[\mathbb{P}[X=k] = \binom{t}{k} r^k (1{-}r)^{t-k},\]

where $X$ is a random variable representing the event that exactly $k$ characters match the pivot, and $r$ is the probability of a character matching the pivot ($r=p$ for a pivot that is a dominating letter; or $r=q$ for non-dominating one).

The above plot shows the distribution when we sample $t=100$ characters. It’s clear that the dominating and non-dominating cases produces two separate curves. We can choose $k$ between these curves as a threshold to determine if we found a dominating letter. In this example, we choose $k\ge20$.

If we want to sample fewer characters, we can set $k$ to a small number. For instance, choosing $k\ge5$ gives us a the cumulative probability:

\[\mathbb{P}[X\ge5] = \sum_{\ell=5}^t \binom{t}{\ell} p^\ell (1-p)^{t-\ell}.\]

This calculation shows that sampling just $t=20$ characters provides a 99.4% confidence level in detecting the dominating letter.

On the other hand, if we plug in $k\ge5$ and $t=20$ for the non-dominating case, we find only a 0.01% probability of producing a false-positive result.

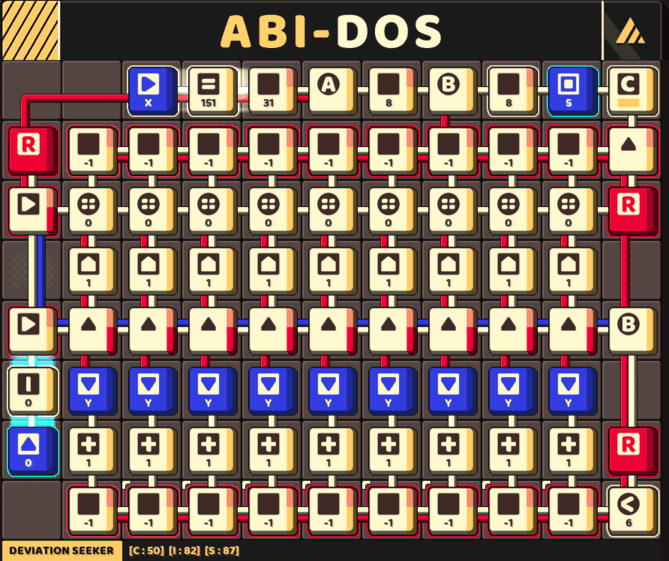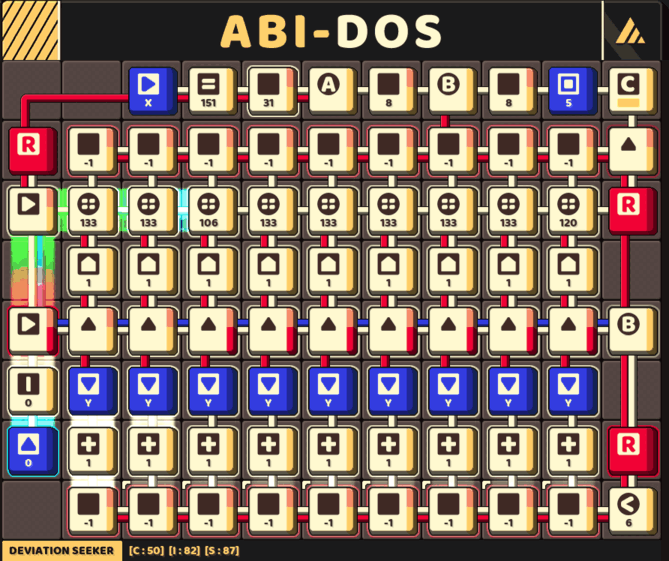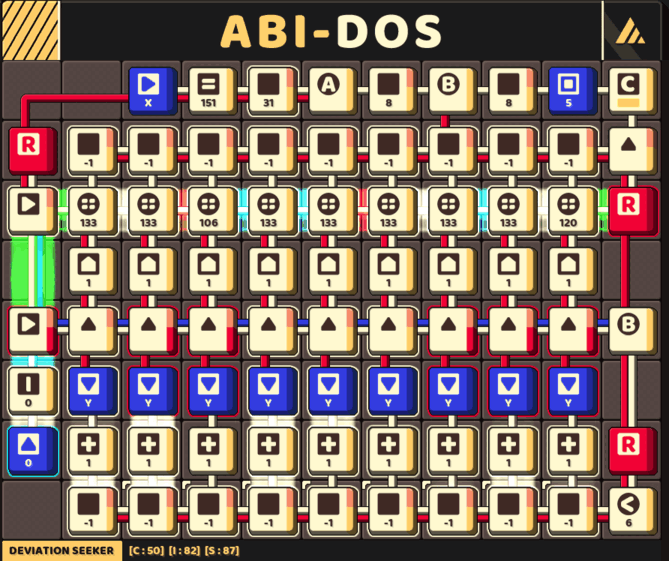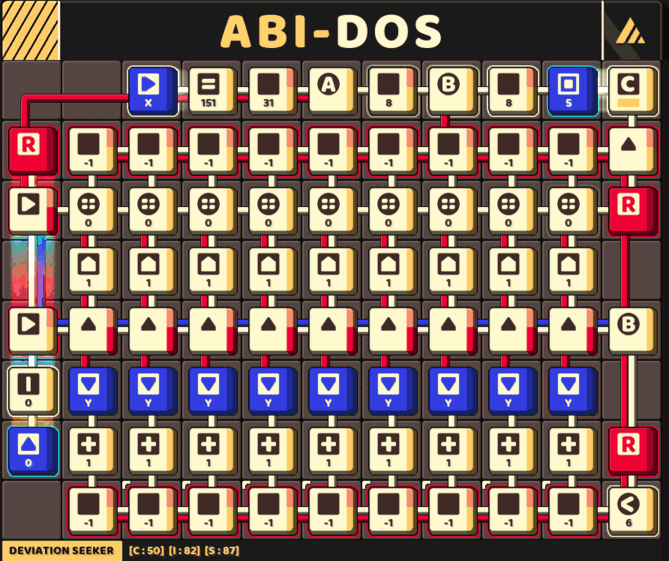
A fast circuit that keep track of 9 pivots

The final challenge is figuring out how to actually implementing a circuit based on this concept, which may result in this gigantic circuit yet highly efficient in running time.

Conclusion

We’ve explored 3 different algorithms to solve the same problem, each with its own unique approach–ranging from deterministic to probabilistic, mechanical to mathematical, and optimized for either space or speed. Each method offers valuable insights into algorithm design and theory behind the scenes.

Which approach do you find most compelling? Can you think of a way to make these algorithms even more efficient, develop a completely new strategy to tackle the problem, or perhaps spot a potential flaw in the design? Feel free to share your thoughts and ideas. I’d love to hear your feedback!