Selected Speed Solutions for MOLEK-SYNTEZ
MOLEK-SYNTEZ was out since late-2019, but I just finish it last month1. The game is about synthesizing realistic molecules2 with fanciful apparatus. It is an open-ended puzzle game that allow players to tackle them in multiple angles, which, for me, subtly begging for speed optimization. Well, I find some of my optimized solutions are beautiful… Maybe you’ll enjoy them too! ⚠️ Lots of large images and spoilers ⚠️
The puzzles are played on a board with finite hexagonal tiles. Each tile can hold one atom, except for the hydrogen that needed to be attach with other larger atom. So the setting reflect organic chemistry (and pharmacy). In each puzzle, we may use any number of base molecules (such as $H_2O$, $H_2SO_4$, $CH_3OH$) to build up a desirable product. However, we only have 6 working hands (in-game named: emitter) to manipulate those molecules. Each hand is a ray from the edge of the playfield that can push, pull, rotate, or delete a molecule; as well as giving and taking a hydrogen from the molecule. With one extra instruction, it can also push a hydrogen from one molecule to another in its trajectory. Thus, if we use this function cleverly, one push-H instruction can replace both take-H and give-H. Result in a better, smaller, faster machine.
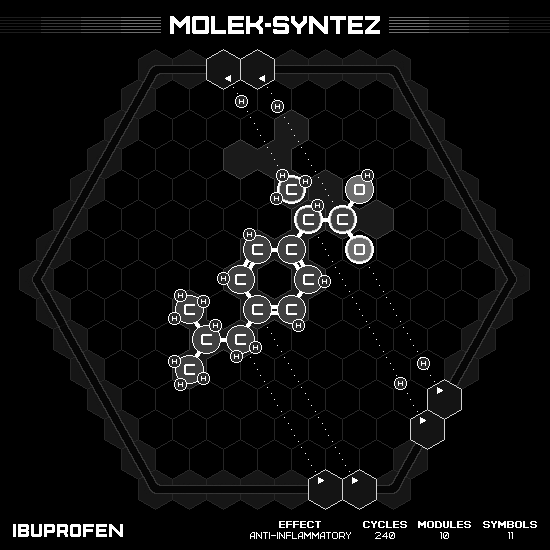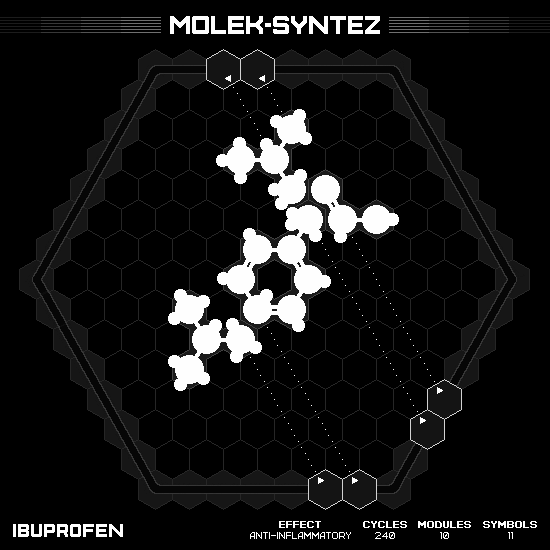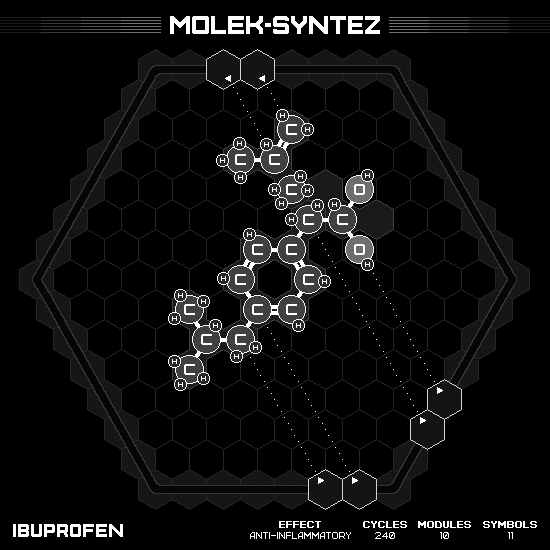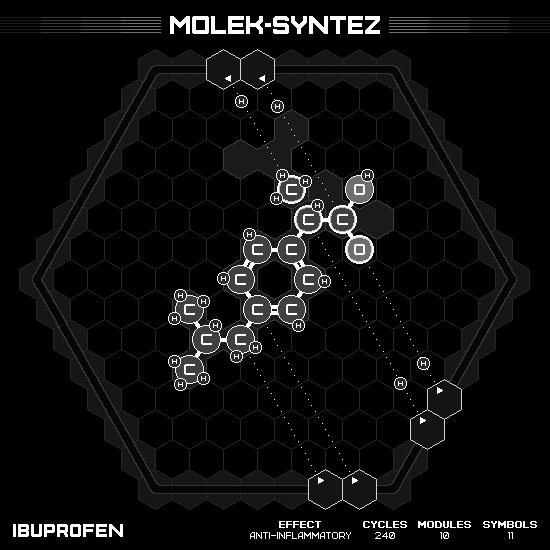
Ibuprofen
This puzzle is almost the simplest non trivial one since it only asks for $C_{13}H_{18}O_2$. The molecule’s structure has a benzene ring in the middle with $RCH_2CHCH_3CH_3$ on one side and $RCHCH_3C{=}OOH$ on the opposite. The center and left parts can be just used directly from the input of toluene $C_7H_8$ and isobutane $C_4H_{10}$. The right side is a bit harder since the most similar input is the formic acid $HC{=}OOH$. So it’s only lack another carbon, which can be get from another isobutane (and delete exceeding). Result in two cycles per product.
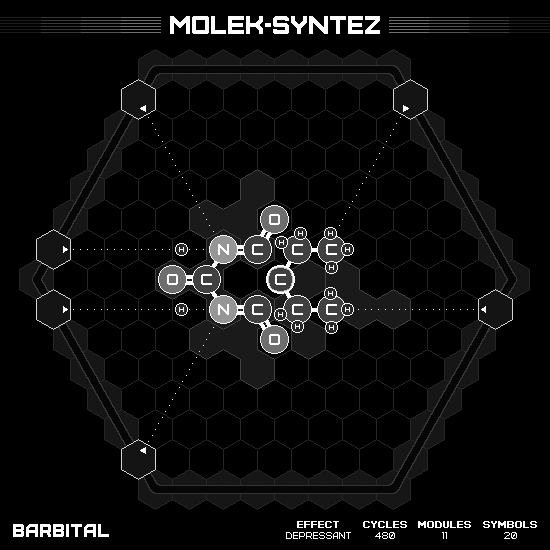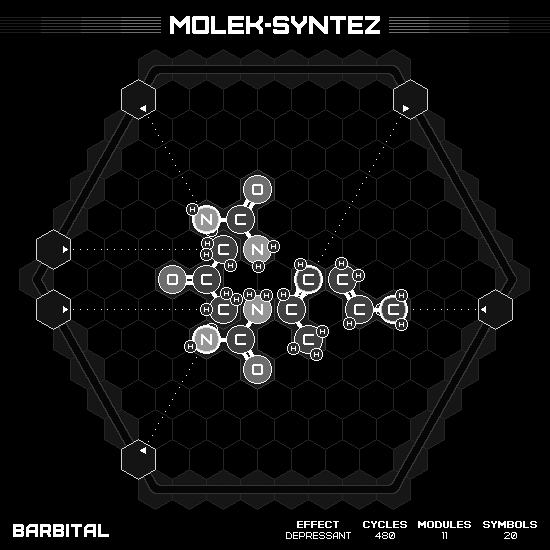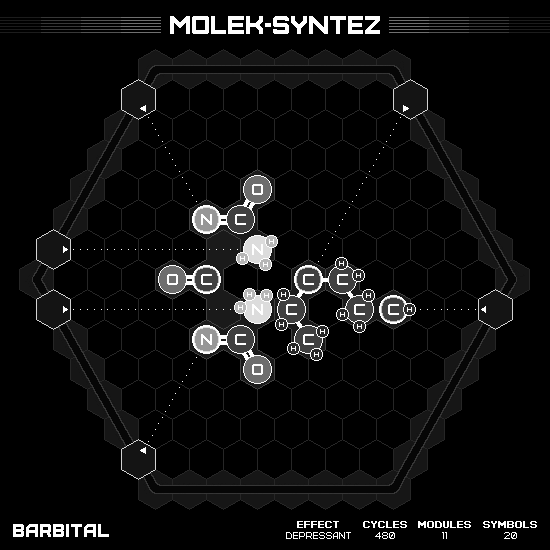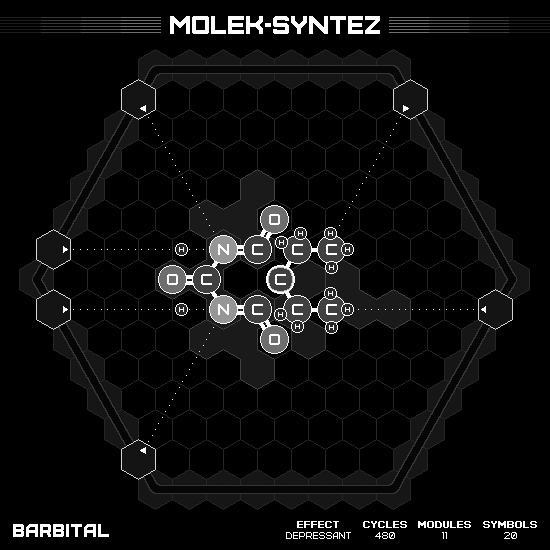
Barbital
This acid has the formula $C_8H_{12}N_2O_3$, where $C_4(NH)_2$ forms a hexagonal ring in the center, with each oxygen grew out of a carbon in the equilateral triangle configuration, and the last carbon has two $RCH_2CH_3$ legs. This molecule is the most symmetrical on 2D structure. And deceiving me to come up with the symmetry solution; however, my working hands seem to unable to manipulate the inner area quick enough. Turn out that I have to break the symmetry and use one way rotation to solve it efficiently.
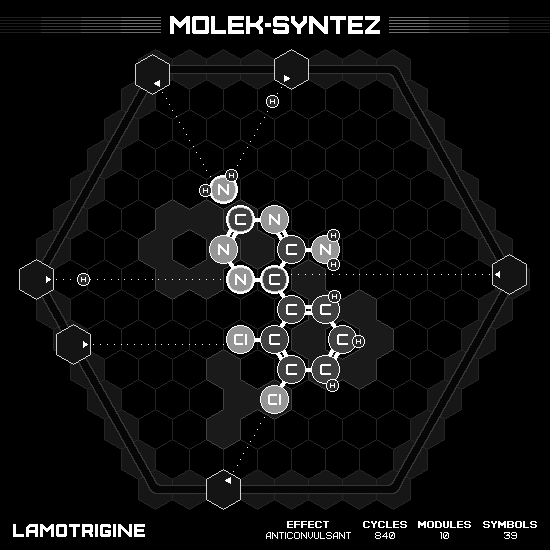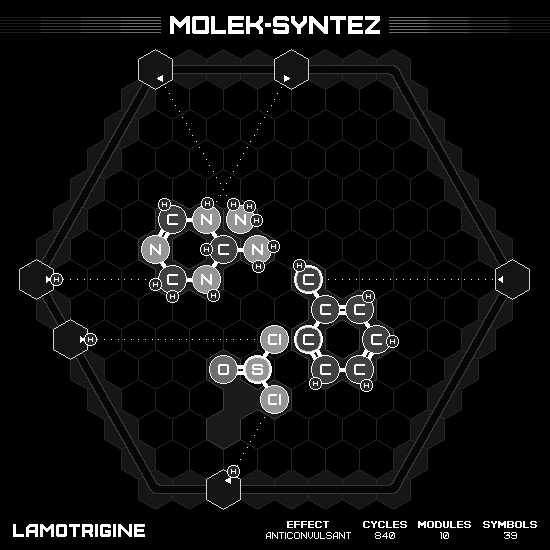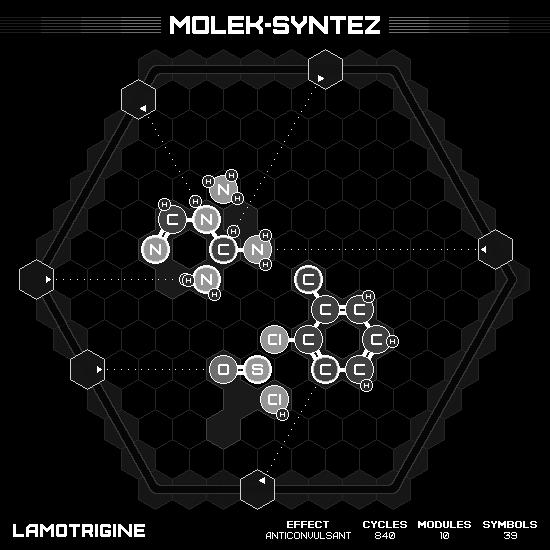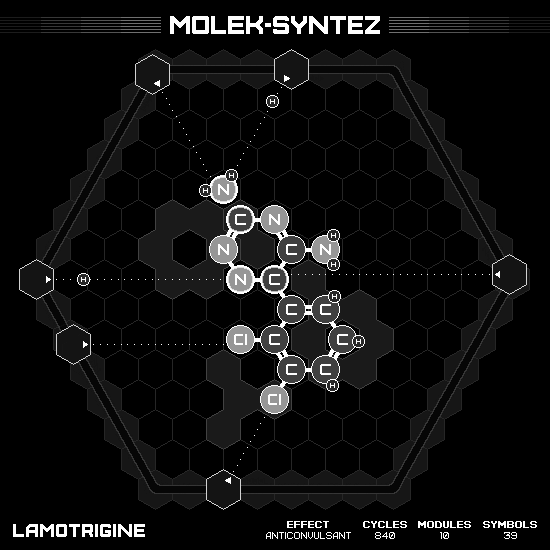
Lamotrigine
The overall structure has two hexagonal rings. The first one is our favorite benzene, which we already has it as an input. The second one required 1,2,4-triazine, however we only have 1,3,5-triazine for the input. So we have to rearrange triazine to have the correct nitrogen order, while maintaining free atoms around the center so it can make bonds. The idea is to slide both rings into each other much faster than normal, otherwise the free atoms are doomed to make bond with undesirable neighbor first. It is succeeded by using two hands to push against each other at the same time.
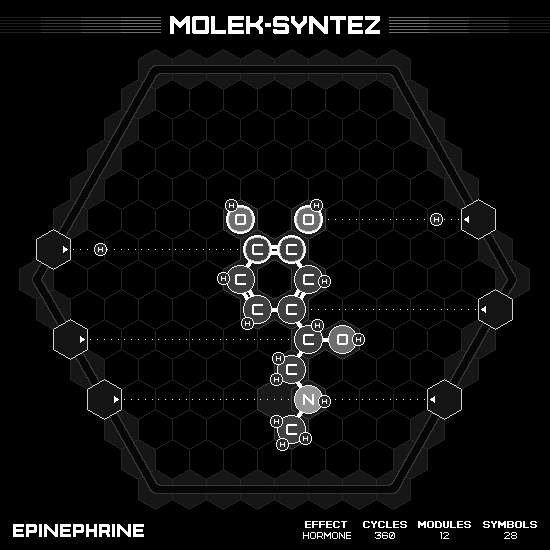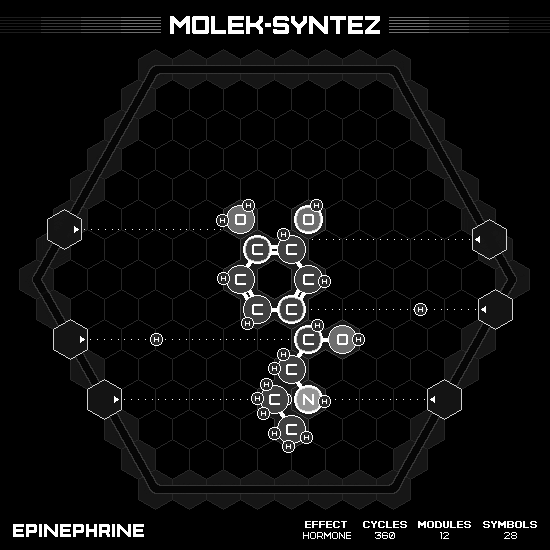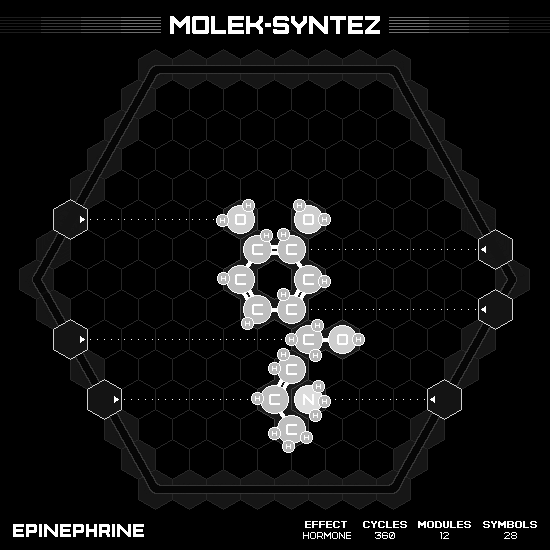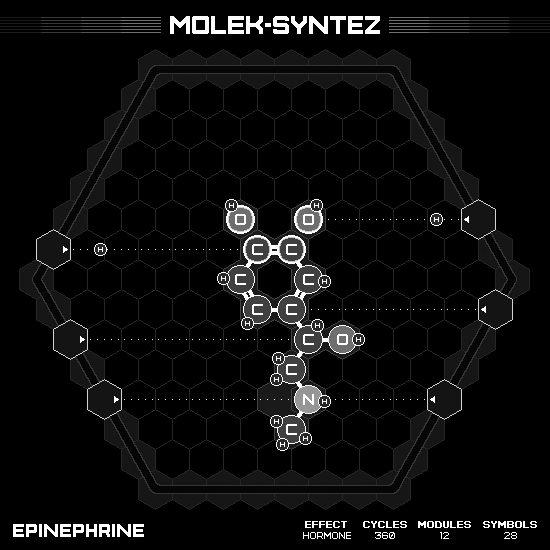
Epinephrine
Wildly known as adrenaline, or with the greedy trademark EpiPen. The formula is $C_9H_{13}NO_3$, with the shape so similar to Y-Unown Pokémon, where the benzene ring is the eye, two oxygen horns above, and a long tail pointing downward. The tail part $RCHOHCH_2NHCH_3$ is easily assembled with 4 emitter hands. But the horn parts pose some challenge since if I remove both hydrogen from the benzene ring at the same time, both carbon in the ring will form a triple bond and refuse to bond with the oxygen later. Thus, I have to alternate taking hydrogen from carbon and oxygen on the opposite side. Normally, this design would require the hands moving back to its initial position before starting the next product, which is not ideal for speed. However, this one can be cheese by identically making another product on the return trip.
Dimercaprol
A twisting molecule $C_3H_8OS_2$, with three carbons serve as a backbone, bonding with oxygen or sulfur each, where the oxygen located in one end. I can make this product in five cycles, but some hands are end up in non-initial location. Thus, I employ the round-trip strategy again. Sadly, I have to use an extra cycle on the way back. Make it total eleven cycles per two products, or 660 cycles in total… Well, it’s not the fastest possible since the leaderboard record otherwise. But hey, 660 cycles! We only need six more, right? 😈
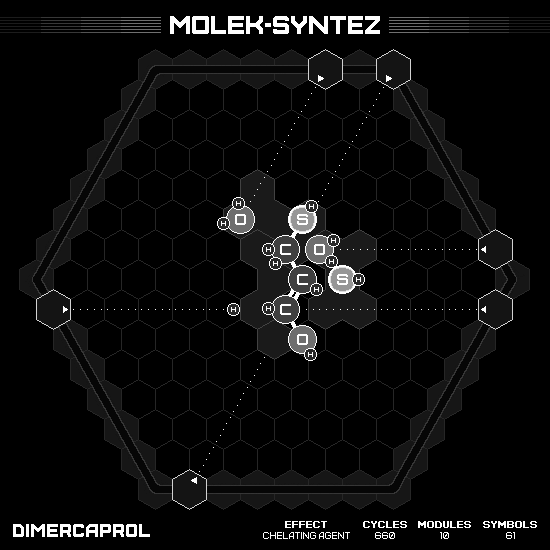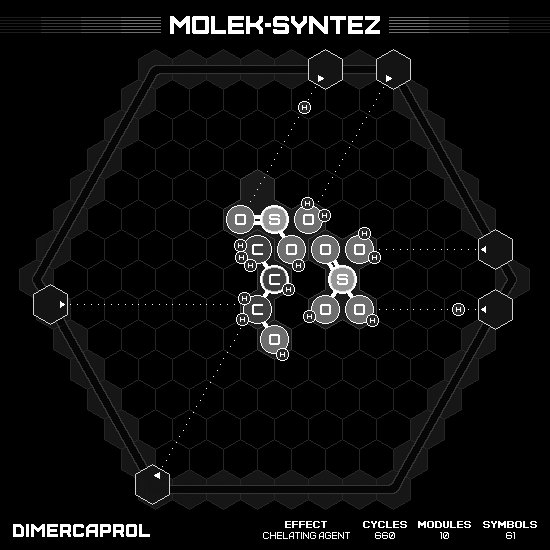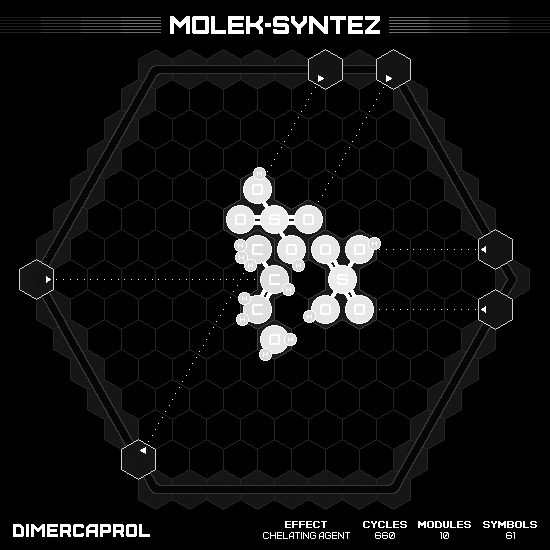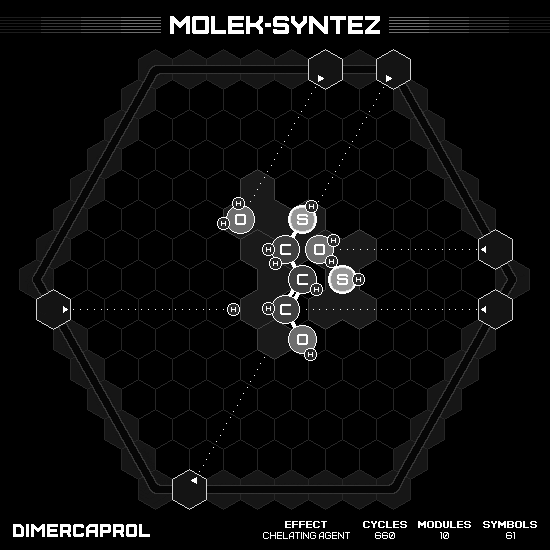
Dimethyl Sulfoxide (DMSO)
A single product can almost be made by only one fixed hand. Working in pair with an identical mirrored hand on the opposite side made this plan possible (like the tale that in heaven, people use long spoons to feed each other). Working in three pairs yield the fastest result, which is a beautiful six-fold symmetry star. No need to describe more 😇

Chloroform
This nice little molecule has a formula $CHCl_3$. My solution use a propene $C_3H_6$ and three hydrochloric acid $HCl$ as the base acid input. At first, I just keep one carbon and delete the others, resulting in one product per two cycles (product in the first cycle then clean up in the second). Later I came to realize that if I only delete one carbon when outputting the first product, I can build another product in two more cycles, with the great benefit that it is also completely reset the playfield. Overall, it is two products in three cycles, where the speed of each product is unequal.
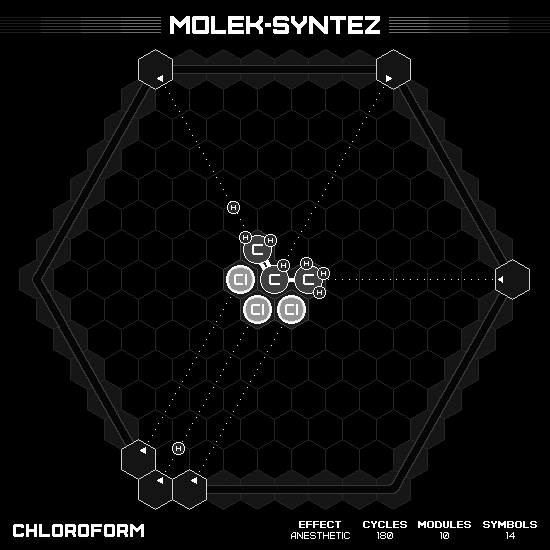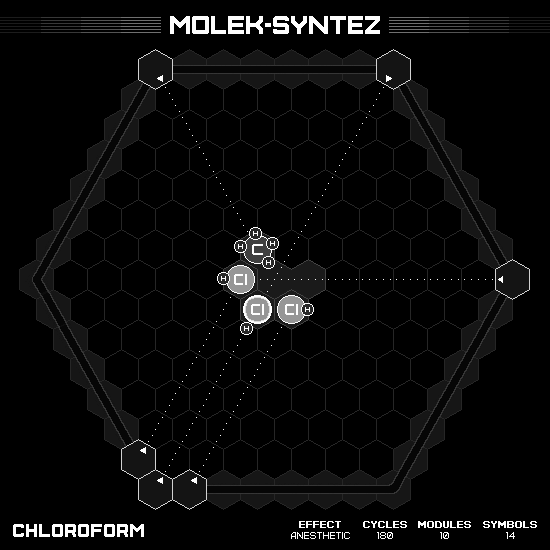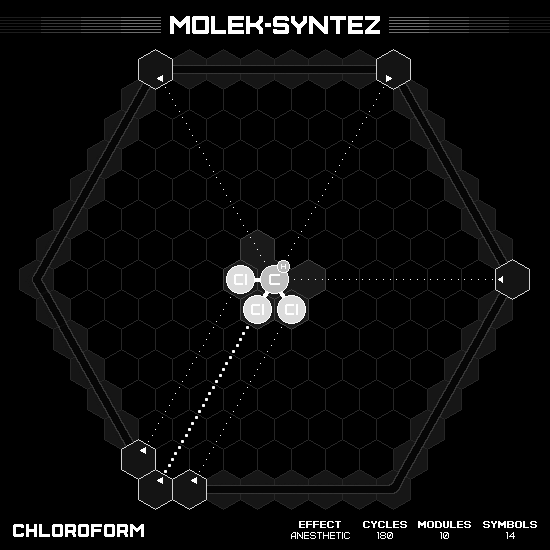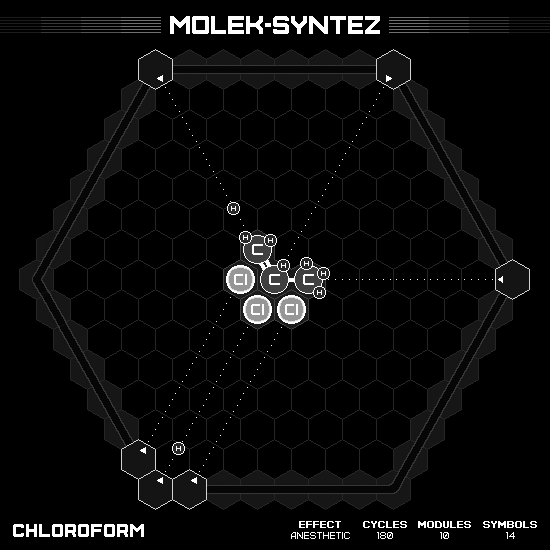
Valnoctamide
The fastest product can be produced in two cycle with only five working hands. The excess hand alone can also produce another product, with the perfect round-trip strategy, in eleven cycles. Thus, by having this two separate mini-machines, I can produce 13 products per 22 cycles, or 204 cycles with the requirement of 120 products.

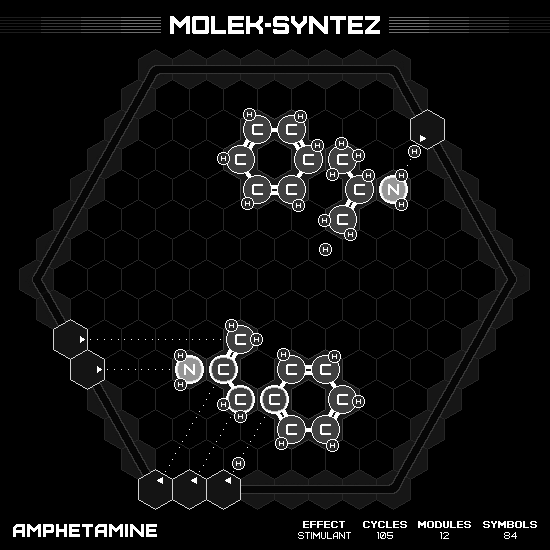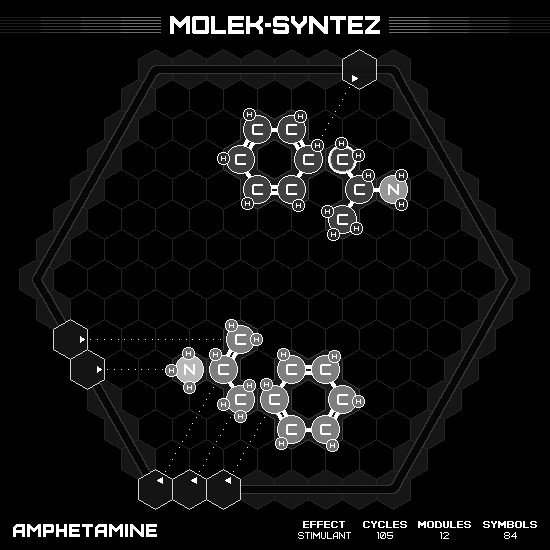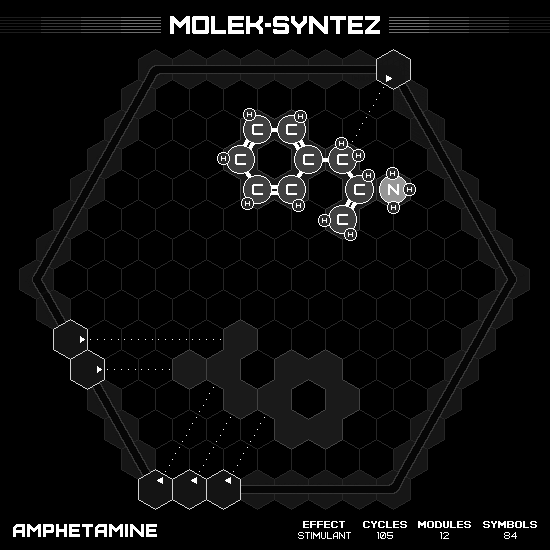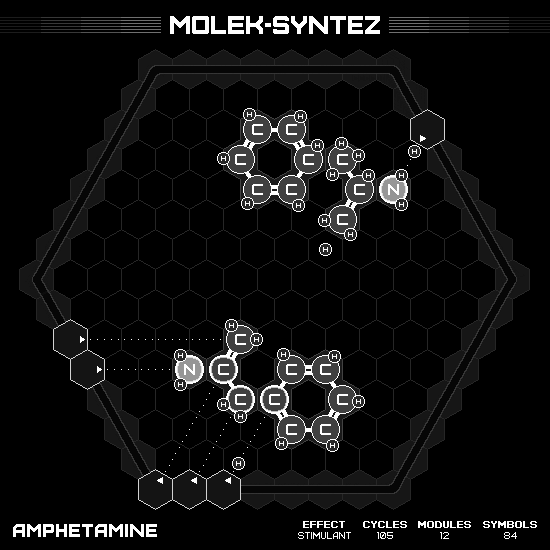
Amphetamine
Employing the separate mini-machines strategy again. The first machine having five hands doing its job in only one cycle. While a free hand produce a product in nine cycles. However, if I occasionally push-H from the fast side, the lone wolf speed will be improves to seven cycles. Thus, the efficiency is eight products in seven cycles, result in the final 105 cycles.
Gamma-Hydroxybutyric Acid (GHB)
Strangely enough, to speed up the solution, the lone wolf here need to delete the middle methanol first. Then, after receiving a new methanol, use push-H to free the carbon from oxygen, bonding with other carbon and leaving the oxygen alone. On sequentially run, the wasted oxygen will prevent the input methanol to appear on board. Which, from now on, we will delete it first in each loop.
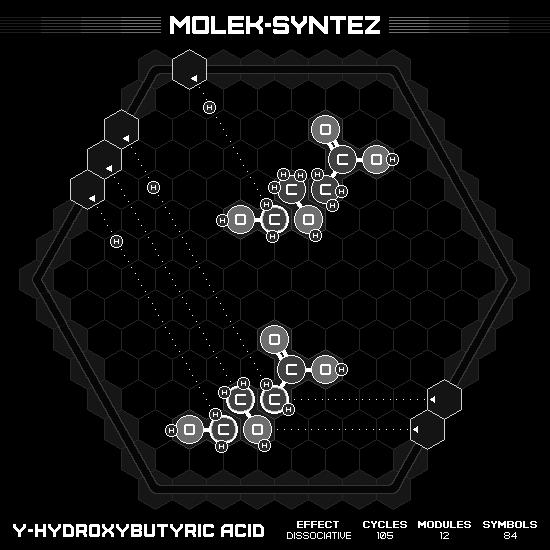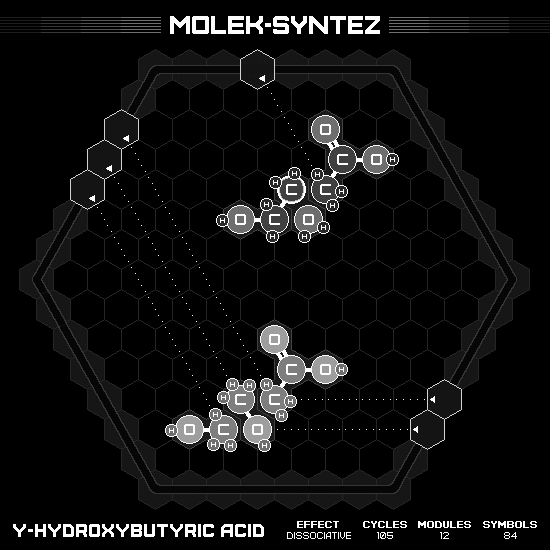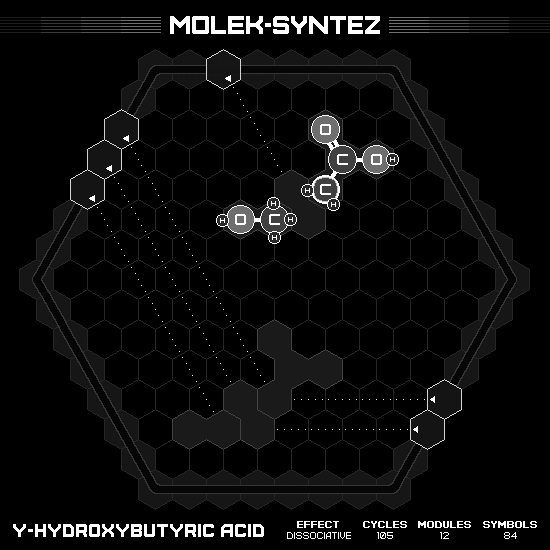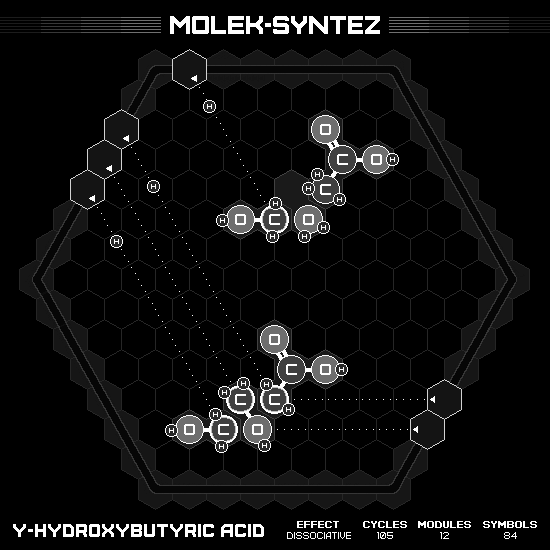
Bithionol
I’m not the fastest on the leaderboard on this one, but I’m sure proud of my machine. It is a wonderful elegant spaceship with two symmetrical humongous warp nacelles. Imagine that this $S(C_6H_3Cl_2O)_2$ goes into our body to eliminates bacteria and parasite!
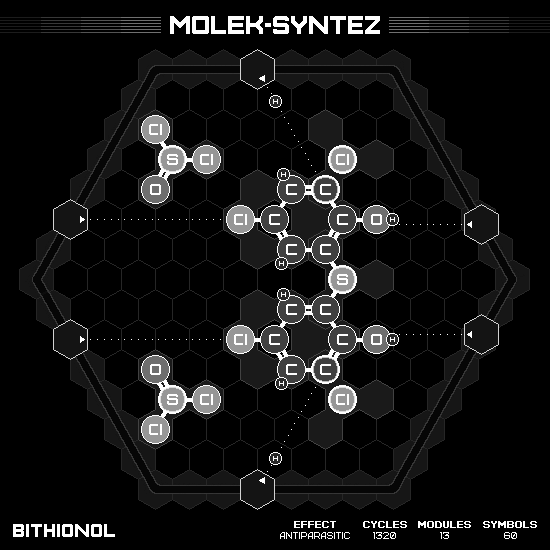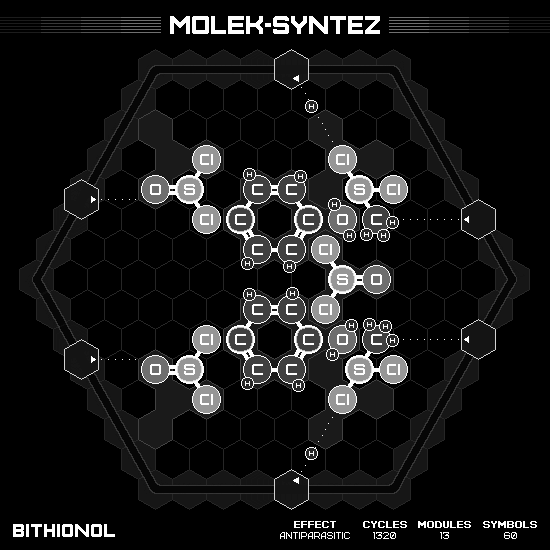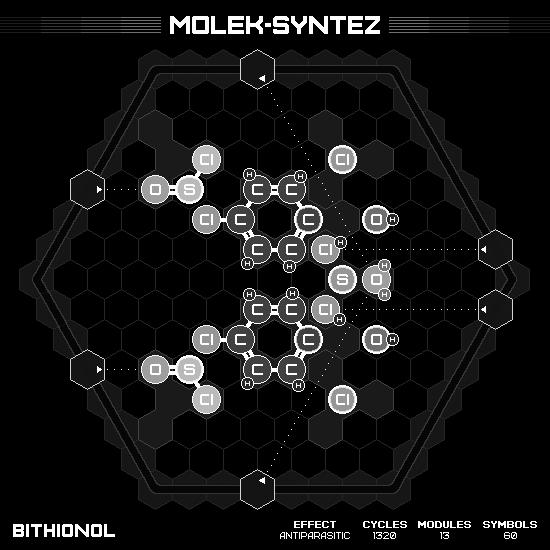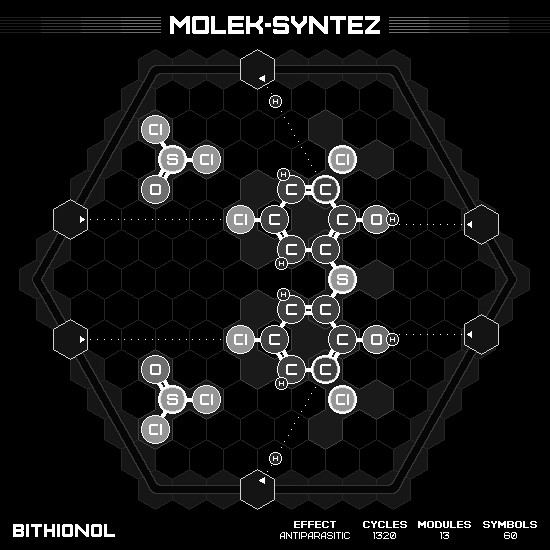
Mebicar
Agreed by the community, it is one of the hardest puzzle in the game, which I succeed optimizing it to some extent. The molecule is symmetry; however, my solution couldn’t manage to fully exploit this aspect. (And too bad that we can’t truly see the pentagonal ring structure due to the limitation of the puzzle.)

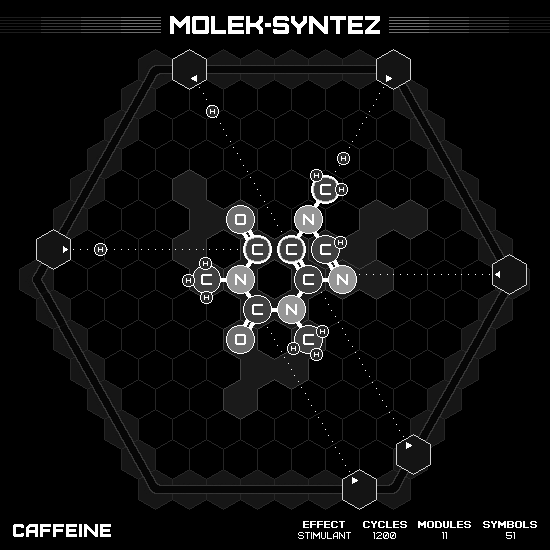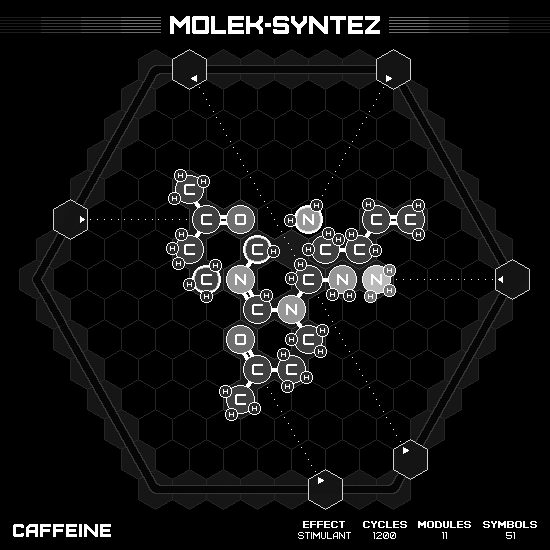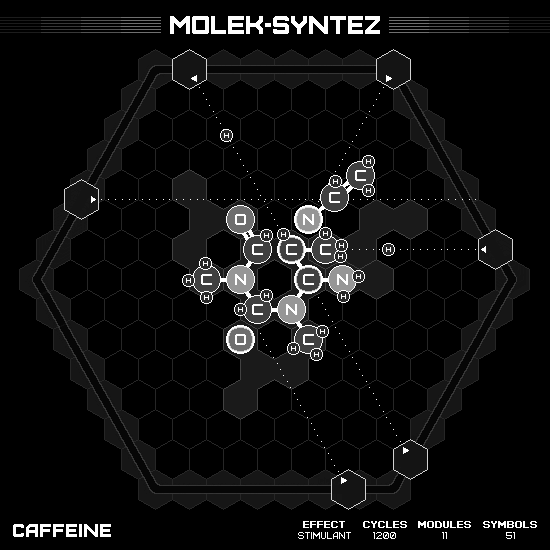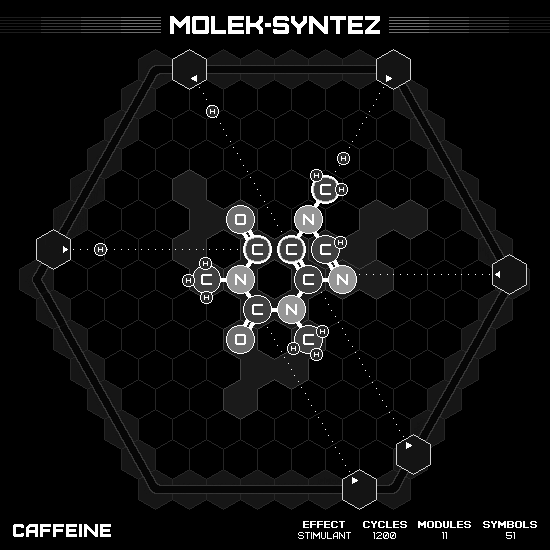
Caffeine
The chemical behind the beloved brewed bitter brown beverage is the very last bonus puzzle in the game. Its molecule compose of two unequal rings that sharing the border. The larger one is a hexagon ring of $C_2(NCH_3CO)_2$, and the smaller one is a pentagon ring of $C_2NCH_3CHN$, with the first two carbon atoms as the shared border. Though it’s not symmetry or anything like other molecules we’ve seen so far, I find this one is the most appealing molecule in the whole game. No, not only this game, but it is the most aesthetic molecule in the entire universe! (I know, I know, I’m only slightly biased here 🤪)

author
