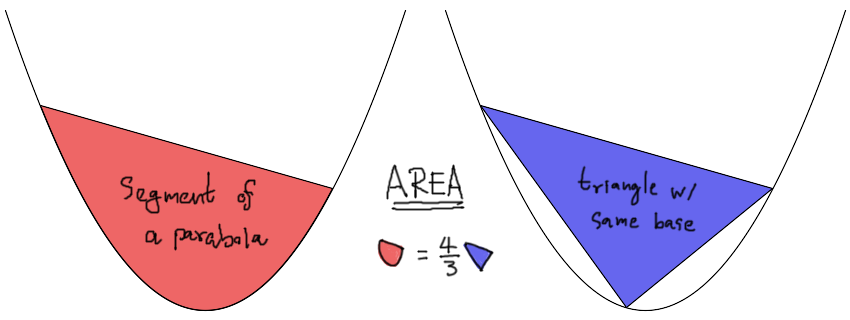
The most popular conic section (except circle that’s seen everywhere) is a parabola. Although nowadays we develop calculus techniques to deal with it, in the time of Archimedes he discovered a beautiful yet simple relationship between an area of the parabola’s segment and an area of the largest inscribed triangle within the segment.

A segment of a parabola is an inner region which enclosed by a straight line and a parabola curve. This concept is similar to the case of circle with chord. In the case of parabola, the segment will have an area $4/3$ times to an area of the triangle with the chord as a base, and another vertex on the parabola curve at the furthest distance from the chord.

To see that the triangle is the largest is easily done via calculus… Actually, the area of the segment can also be found via calculus too! But that will spoiled the fun. We’ll try use do it almost like the way Archimedes did it back in the good old day (cuz we gonna apply the modern coordinate lol).

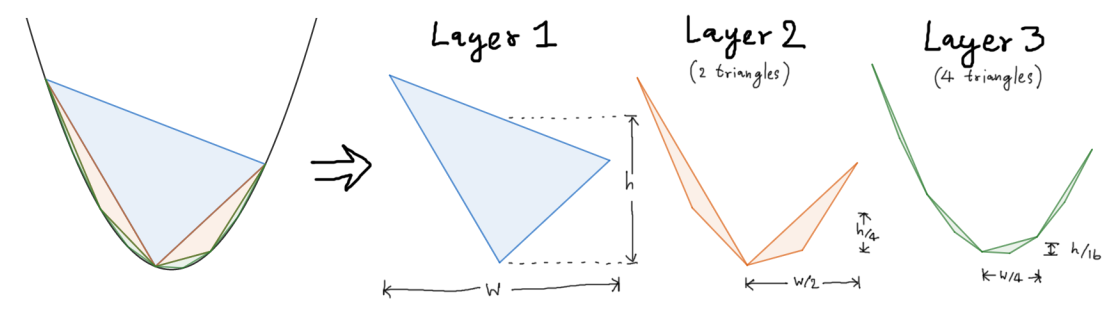
The main idea behind Archimedes’ method is the recursion. That is we’ll partition the main problem into sub problems, solve the top layer, apply to bottoms. In this case we will split parabola’s segment by the largest triangle, which will produce two more segments of the smaller size. Split them to gain more and more triangles. Finally, we can say that the sum of all area of triangles is the area of the segment.

Zooming animation of the inscribed triangles that layering the segment. The rate of zooming between horizontal and vertical is not the same to preserve the shape of the parabola.

So the main problem is to find an area of the largest first-layer triangle. How to do that?

Since we know that every parabola is similar, and by resizing we can make every parabola equivalent (like circle, unlike ellipse/hyperbola). To simplify the matter, we’ll consider only the simplest parabola, the one with the formula $f(x)=x^2$.

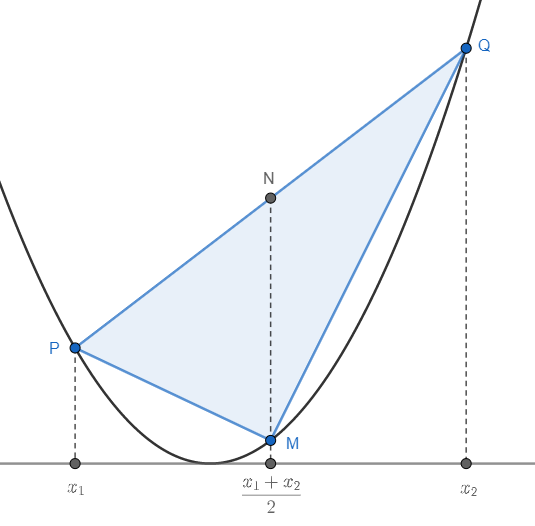
Important points on the triangle inscribed within the segment

Let the chord intersect parabola at $P$ and $Q$, which projected to $x_1$ and $x_2$ on the horizontal axis respectively. Hence,

\[\begin{align} P &= \left( x_1, f(x_1) \right) = \left( x_1, x_1^2 \right), \\ Q &= \left( x_2, f(x_2) \right) = \left( x_2, x_2^2 \right). \end{align}\]

We’ll find $M$, another vertex of the triangle. Which lies in the middle between $x_1$ and $x_2$ on the horizontal axis, and land on the curve of the parabola. In other words,

\[\begin{align} M &= \left( \frac{x_1+x_2}2, f\left( \frac{x_1+x_2}2 \right) \right) \\ &= \left( \frac12(x_1+x_2), \frac14 ( x_1 + x_2 )^2 \right). \end{align}\]

Since we know all the points of the triangle, it is easy to find an area. But that’s might take the fun away. So we’ll adapt the simple well-known formula for finding triangle area, that is the width of the base times the height to the vertex (and then half). It is natural to use $\overline{PQ}$ as the base and $M$ as the vertex.

However, if we measure the length of the tilted chord $\overline{PQ}$ directly, the following calculation might get too complicate real quick. We’ll measure the length of $\overline{PQ}$ after projection onto horizontal axis instead. Which gives us a simple value

\[w = \abs{x_1 - x_2}. \tag{1}\label{width}\]

We have to change the way to measure the height of the triangle too. That is we’ll construct a perpendicular line to the horizontal axis. Then find the intersections on $\overline{PQ}$ such that the line is also pass the vertex $M$. Let that intersect point be $N$. We’ll see that $N$ is also the midpoint of $\overline{PQ}$. Specifically,

\[N = \left( \frac12(x_1+x_2), \frac12(x_1^2+x_2^2) \right).\]

Thus, $\overline{MN}$ is the height of the triangle that we want. Which has the value of

\[\begin{align} h &= \abs{\frac12(x_1^2+x_2^2) - \frac14(x_1+x_2)^2} \\ &= \frac14\abs{x_1-x_2}^2. \tag{2}\label{height} \end{align}\]

From $\eqref{width}$ and $\eqref{height}$, we’ll have the area of the triangle

\[\hat{A} = \frac18 \abs{x_1-x_2}^3. \tag{3}\label{area}\]

This is the area of the largest triangle. Observe that we can also calculate areas for other sub-triangles in the same manner. For example, to find an area of a triangle in the next layer, we know that the width is half and the height is a quarter. So the smaller triangle must have an area one eighth to the area of the main triangle.

Decomposition of inscribed triangles by layers

But don’t forget that the next layer have more triangle than the previous one. Because the process of splitting segments gives us two more smaller segments. So the total area of the next layer will be different from the previous layer by only four times.

Now we arrived at the conclusion that the area of the parabola’s segment, $\breve{A}$, can be find via this infinite sequence

\[\breve{A} = \left( 1 + \frac14 + \frac1{4^2} + \frac1{4^3} + \cdots \right) \hat{A}.\]

Which easily proven via algebra. But I bet it’s more fun using proof without words 😊