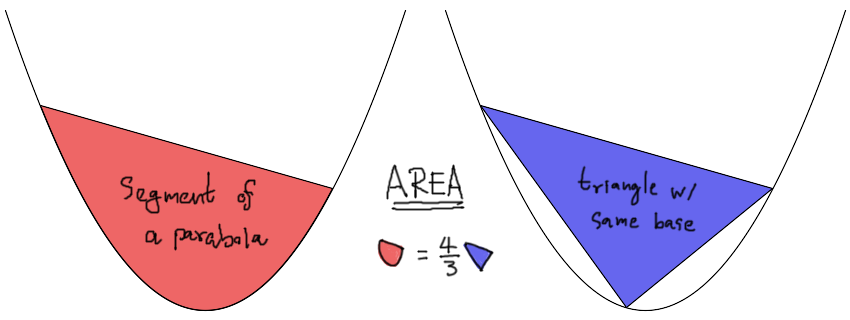
ภาคตัดกรวยยอดนิยม (ถ้าไม่นับวงกลมที่เห็นไปทั่ว) ก็คงหนีไม่พ้นพาราโบลา แม้ทุกวันนี้เราจะมีเทคนิคทางแคลคูลัสสำหรับเล่นกับพาราโบลาอย่างมากมาย แต่ในสมัยของอาร์คิมีดีสนั้นเขาได้ค้นพบความสัมพันธ์อันเรียบง่ายสวยงามระหว่างพื้นที่ของเซกเมนต์พาราโบลาและพื้นที่สามเหลี่ยมแนบในเซกเมนต์ที่ใหญ่ที่สุด

เซกเมนต์พาราโบลาเกิดจากการเอาเส้นตรงมาตัดโค้งพาราโบลาที่สองจุดแล้วหาพื้นที่ในส่วนปิดกั้น ซึ่งจะคล้ายๆ กับกรณีวงกลมที่เราจะเรียกเส้นตัดว่าคอร์ดและเรียกพื้นที่ปิดกั้นว่าเซกเมนต์ โดยกรณีของพาราโบลานี้ เซกเมนต์ดังกล่าวจะมีพื้นที่เป็น $4/3$ เท่าของพื้นที่สามเหลี่ยมแนบในที่มีฐานเป็นเส้นคอร์ด และมีจุดยอดอยู่บนโค้งพาราโบล่าที่ห่างตั้งฉากออกไปจากเส้นคอร์ดเส้นนั้นไกลที่สุดนั่นเอง

ประเด็นว่าสามเหลี่ยมแนบในดังกล่าวคือสามเหลี่ยมที่ใหญ่ที่สุดนั้นสามารถเห็นได้ไม่ยากด้วยวิธีทางแคลคูลัส … เอาจริงๆ การหาพื้นที่พาราโบลาก็ทำได้โดยง่ายด้วยแคลคูลัสเช่นกัน แต่เดี๋ยวไม่เร้าใจ งั้นเรามาพิสูจน์ด้วยวิธีกึ่งๆ อาร์คิมีดีสด้วยกันดีกว่า (เพราะเราจะใช้การอัดแกนซึ่งเป็นเครื่องมือทรงพลังสมัยใหม่เข้าช่วย 55555)

แนวคิดหลักของวิธีการแบบอาร์คิมีดีส จะเป็นไปในแนวทางแบบการเรียกตัวเอง (recursion) คือเราจะแบ่งปัญหาหลักเป็นปัญหาย่อยที่ซ้อนกันเป็นชั้นๆ แก้ปัญหาในชั้นบนสุดให้เรียบร้อย แล้วประยุกต์เอาความรู้นั้นไปแก้ปัญหาชั้นล่างๆ ลงไปโดยอัตโนมัติ ซึ่งในกรณีนี้ก็คือเราจะตัดแบ่งเซกเมนต์หลักด้วยสามเหลี่ยมชิ้นใหญ่ ซึ่งจะทำให้ได้เซกเมนต์ย่อยสองข้าง แล้วจึงตัดเซกเมนต์ย่อยๆ ด้วยสามเหลี่ยมชิ้นเล็กๆ แบบเดิมลงไปเรื่อยๆ ดังนั้นเมื่อเราหาผลรวมของพื้นที่สามเหลี่ยมทุกชิ้นก็จะได้พื้นที่ของเซกเมนต์หลักนั่นเอง

อนิเมชันซูมสามเหลี่ยมแนบในพาราโบลาที่แบ่งเซกเมนต์เป็นชั้นๆ โดยซูมแกนตั้งกับนอนด้วยความเร็วไม่เท่ากันเพื่อคงรูปร่างโค้งพาราโบลาเอาไว้

เพราะงั้นปัญหาหลักของเราคือการหาพื้นที่สามเหลี่ยมชิ้นแรกสุดให้ได้ก่อน แล้วเราจะทำได้อย่างไร?

เนื่องจากเรารู้ว่าพาราโบลาทุกชิ้นนั้น เมื่อนำไปขยาย/ลดขนาดแล้วมันจะสมมูลกันหมด (เช่นเดียวกับวงกลม, ต่างจากกรณีวงรี/ไฮเปอร์โบลา) ดังนั้นเพื่อความสะดวก เราจะพิจารณาเฉพาะพาราโบลาที่เรียบง่ายที่สุด คือตัวที่มีสมการเป็น $f(x) = x^2$ ก็ควรจะเพียงพอ

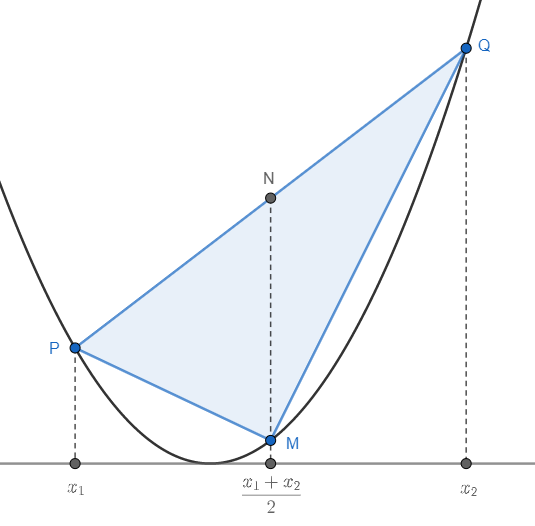
จุดสำคัญต่างๆ ของสามเหลี่ยมแนบในเซกเมนต์ของพาราโบลา

ให้คอร์ดที่เราสนใจตัดพาราโบลาตัดที่จุด $P$ และ $Q$ ซึ่งถูกฉายลงมายังแกนนอน ณ ตำแหน่ง $x_1$ และ $x_2$ ตามลำดับ ดังนั้น

\[\begin{align} P &= \left( x_1, f(x_1) \right) = \left( x_1, x_1^2 \right) \\ Q &= \left( x_2, f(x_2) \right) = \left( x_2, x_2^2 \right) \end{align}\]

เราจะสร้างจุด $M$ ซึ่งเป็นจุดยอดอีกจุดของสามเหลี่ยม โดยมันคือจุดกึ่งกลางระหว่าง $x_1$ และ $x_2$ ในแนวนอน และมีความสูงไปอยู่บนพาราโบลาพอดี หรือก็คือ

\[\begin{align} M &= \left( \frac{x_1+x_2}2, f\left( \frac{x_1+x_2}2 \right) \right) \\ &= \left( \frac12(x_1+x_2), \frac14 ( x_1 + x_2 )^2 \right) \end{align}\]

รู้ตำแหน่งที่แน่ชัดของจุดยอดทั้งสามจุดก็สามารถหาพื้นที่สามเหลี่ยมได้ไม่ยาก แต่นั่นอาจจะทำให้เราพลาดอะไรสนุกๆ ไป เราจะประยุกต์ใช้วิธีหาพื้นที่อันเรียบง่ายที่เรารู้จักกันดีมาตั้งแต่มัธยม ซึ่งก็คือ เอาความกว้างฐานคูณความสูงถึงจุดยอด (แล้วหารสอง) เราจะใช้ส่วนของเส้นตรง $\overline{PQ}$ เป็นฐานและให้ $M$ เป็นจุดยอด

ถ้าเราวัดความกว้างตามแนวเฉียงของ $\overline{PQ}$ นั้นจะทำให้การคำนวณระหว่างทางยุ่งยากจนเกินไป เราจะเปลี่ยนไปวัดความยาวของ $\overline{PQ}$ เมื่อมันถูกฉายลงมายังแกนนอนแทน จะได้ว่าความกว้างที่เราสนใจก็คือ

\[w = \abs{x_1 - x_2} \tag{1}\label{width}\]

เมื่อเราวัดความกว้างแบบเอียงๆ เช่นนั้น เราต้องเปลี่ยนวิธีวัดความสูงอีกนิดหน่อยด้วย ซึ่งก็คือเราจะลากเส้นตรงที่ตั้งฉากกับแกนนอน แล้ววัดความสูงจากจุดยอดไปจนถึงฐานที่เอียงๆ อันนั้น ให้จุดที่เส้นลากไปถึงฐานเป็นจุด $N$ จะได้ว่า $N$ เป็นจุดกึ่งกลางระหว่าง $\overline{PQ}$ พอดี หรือได้ว่า

\[N = \left( \frac12(x_1+x_2), \frac12(x_1^2+x_2^2) \right)\]

ดังนั้น $\overline{MN}$ ก็คือความสูงของสามเหลี่ยมที่เราต้องการวัด และมันมีค่าเท่ากับ

\[\begin{align} h &= \abs{\frac12(x_1^2+x_2^2) - \frac14(x_1+x_2)^2} \\ &= \frac14\abs{x_1-x_2}^2 \tag{2}\label{height} \end{align}\]

จาก $\eqref{width}$ และ $\eqref{height}$ จึงได้ว่าพื้นที่ของสามเหลี่ยมนี้คือ

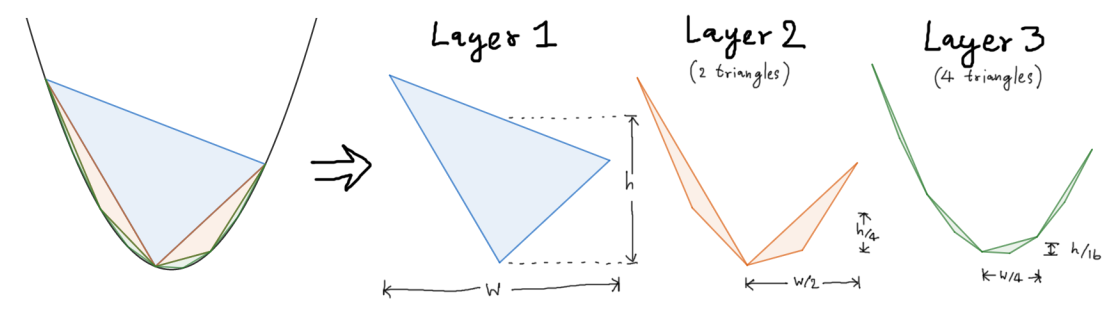
\[\hat{A} = \frac18 \abs{x_1-x_2}^3 \tag{3}\label{area}\]

นั่นคือพื้นที่สามเหลี่ยมชิ้นที่ใหญ่ที่สุดหนึ่งรูป ซึ่งเราจะเห็นว่าสามารถคิดพื้นที่สามเหลี่ยมรูปอื่นๆ ได้ในทำนองเดียวกันอีกด้วย อย่างเช่นเมื่อเราต้องการหาพื้นที่สามเหลี่ยมย่อยในชั้นถัดมา จะเห็นว่าวิธีวัดความกว้างของเรานั้นวัดความกว้างได้เป็นครึ่งหนึ่งของสามเหลี่ยมรูปเดิม และวัดความสูงได้เป็นหนึ่งในสี่เท่า ดังนั้นสามเหลี่ยมรูปที่เล็กลงมานี้จึงมีพื้นที่เล็กลงไปแปดเท่านั่นเอง

สามเหลี่ยมชั้นต่างๆ ที่แบ่งเซกเมนต์ของพาราโบลาลงไปเรื่อยๆ

แต่อย่าลืมว่าสามเหลี่ยมชั้นถัดมานั้นมีจำนวนเยอะกว่าสามเหลี่ยมชั้นก่อน เพราะว่าวิธีการตัดเซกเมนต์ชั้นหนึ่งๆ ของเรานั้นทำให้ได้เซกเมนต์ใหม่เป็นสองเท่าเสมอ ดังนั้นพื้นที่สามเหลี่ยมรวมกันในแต่ละชั้นจึงต่างจากชั้นก่อนหน้าแค่สี่เท่าเท่านั้น

นั่นก็คือเราจะสรุปได้ว่าพื้นที่เซกเมนต์พาราโบลา $\breve{A}$ สามารถหาได้จากอนุกรมอนันต์ เช่นนี้

\[\breve{A} = \left( 1 + \frac14 + \frac1{4^2} + \frac1{4^3} + \cdots \right) \hat{A}\]

ซึ่งจะพิสูจน์เชิงสมการก็ทำได้ไม่ยากอีกเช่นกัน แต่ถ้ายังอยากสนุกจะลองให้เหตุผลเชิงรูปภาพก็ย่อมได้ 😊