$S_k(n) = 1^k + 2^k + 3^k + \cdots + n^k$
เคยสงสัยมานานแล้วว่า ผลรวมของจำนวนเต็มที่ถูกยกกำลังด้วยค่าคงที่ $1^k + 2^k + 3^k + \cdots + n^k$ สำหรับทุกๆ $k \in \mathbb{N}$ มันจะมีสูตรหน้าตาเป็นอย่างไร ซึ่งถ้าดูกรณีที่ง่ายที่สุดอย่าง $k=1$ เราก็จะมีวิธีพิสูจน์อันแสนสวยงามผ่านการวาดภาพเช่นนี้
บทพิสูจน์ด้วยภาพว่า $1 + 2 + 3 + \cdots + n = n(n+1)/2$
และจากแนวทางการพิสูจน์เช่นนี้ จึงทำให้เราเรียกสูตรในกรณีที่ $k=1$ ว่าจำนวนสามเหลี่ยมนั่นเอง
แม้มนุษยชาติจะทราบสูตรข้างต้นย้อนกลับไปได้ตั้งแต่สมัยกรีกโบราณแล้ว แต่ตำนาน (อันอาจเป็นเท็จ) ที่น่าตื่นตาตื่นใจของสูตรดังกล่าว คงหนีไม่พ้นเรื่องเล่าที่ว่าเจ้าหนู Gauss เมื่อครั้งยังเยาว์วัยนั้นสามารถแก้โจทย์ $1+2+3+\cdots+100$ ได้อย่างรวดเร็ว ทั้งที่คุณครูผู้อยากอู้งานได้เขียนโจทย์ขึ้นมาอย่างลวกๆ เพื่อหวังให้เด็กๆ วุ่นวายอยู่กับมันจนหมดคาบเรียนนั่นแหละ
กลับมาดูกรณีที่ $k=2$ จะเห็นว่าเราก็มีวิธีพิสูจน์ด้วยการวาดภาพ (และตั้งชื่อให้) ในทำนองเดียวกัน
บทพิสูจน์แบบโต้ตอบด้วยภาพว่า $1^2 + 2^2 + 3^2 + \cdots + n^2 = n(n+1)(2n+1)/6$
ซึ่งทำให้เราได้สูตรที่สวยงามน่าสนใจออกมา ยิ่งเมื่อดูควบคู่กับสูตรจากกรณีก่อนหน้า เราอาจจะเดาว่าสูตรของกรณีต่อไปๆ ก็น่าจะมีโครงสร้างที่อิงบนคำตอบเดิม คือน่าจะเขียนได้ประมาณว่า
\[S_k(n) \stackrel?= \frac{n(n+1)(2n+1)\cdots(???)}{(k+1)!}\]แต่เราจะรู้ได้อย่างไรว่าสูตรหน้าตาเช่นนี้มันถูกต้อง เพราะจากเทคนิคการวาดภาพเพื่อช่วยพิสูจน์ จะเห็นว่าเมื่อเราต้องการพิสูจน์กรณี $k$ ที่สูงขึ้นไป เราก็ยิ่งต้องใส่มิติเพิ่มขึ้นเป็นเงาตามตัว … ซึ่งสำหรับมนุษย์โดยทั่วไปก็น่าจะจินตนาการตามไม่ไหวแล้ว (หละมั้ง?)
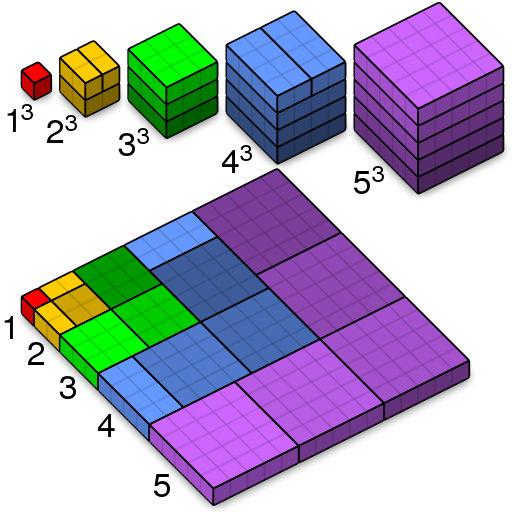
บทพิสูจน์ด้วยภาพว่า $1^3 + 2^3 + 3^3 + \cdots + n^3 = (1 + 2 + 3 + \cdots + n)^2$
โอเคว่ามันยังพอมีทริกที่จะหลบเลี่ยงประเด็นด้านมิติที่สูงเกินจะเข้าใจได้บ้าง แต่เทคนิคเหล่านั้นแต่ละอันนั้นก็ดูจะเป็นการแก้ปัญหาเฉพาะหน้าที่ไม่สามารถนำไปใช้กับกรณีทั่วไปได้เลย จึงทำให้การพิสูจน์ด้วยภาพเช่นนี้ไม่เหมาะสมอีกต่อไป
อนึ่ง แค่กรณีที่ $k=3$ ก็ทำให้เราเห็นแล้วว่า สูตรที่เราเฝ้าฝันหวานอยากได้ในข้างต้นนั้น มันไม่ได้ถูกต้องเข้าใกล้ความเป็นจริงเลยแม้แต่นิดเดียว 😭
งั้นก็ต้องมาลุยกับสมการตรงๆ โดยพระเอกที่จะมาร้อยเรียงเรื่องราวบทพิสูจน์ของเรา ก็คือการกระจายทวินามที่เราคุ้นเคยกันดี
\[(a+1)^{k+1} = a^{k+1} + \binom{k+1}k a^k + \cdots + \binom{k+1}2 a^2 + \binom{k+1}1 a + 1\]ต่อไปเราจะสร้าง $f_k(a) = (a+1)^{k+1} - a^{k+1}$ สังเกตว่า $\sum f_k(a)$ นั้นสามารถถูกจัดการได้สองทาง ในทางที่หนึ่งคือเราจะใช้เทคนิคอนุกรมกล้องส่องทางไกล เพื่อย่นระยะห่างระหว่างพจน์แรกกับพจน์สุดท้ายด้วยการทำลายพจน์กลางๆ ทิ้งไป
\[\begin{align} \sum_{a=1}^n f_k(a) &= \left( (n+1)^{k+1} - n^{k+1} \right) + \cdots + \left( 3^{k+1} - 2^{k+1} \right) + \left( 2^{k+1} - 1 \right) \\ &= (n+1)^{k+1} - 1 \\ &= n^{k+1} + \binom{k+1}k n^k + \cdots + \binom{k+1}2 n^2 + \binom{k+1}1 n \label{eq:telescope}\tag{1} \end{align}\]ส่วนอีกทางเราจะทำการกระจายทวินามแต่ละ $f_k(a)$ ก่อน แล้วค่อยจับกลุ่มรวมพจน์ตัวที่เลขชี้กำลังเท่ากัน
\[\begin{align} \sum_{a=1}^n f_k(a) &= \sum_{a=1}^n \left( \binom{k+1}k a^k + \cdots + \binom{k+1}2 a^2 + \binom{k+1}1 a + 1 \right) \\ &= \binom{k+1}k \! \left( \sum_{a=1}^n a^k \right) + \cdots + \binom{k+1}1 \! \left( \sum_{a=1}^n a \right) + \left( \sum_{a=1}^n 1 \right) \\ &= \binom{k+1}k S_k(n) + \cdots + \binom{k+1}2 S_2(n) + \binom{k+1}1 S_1(n) + S_0(n) \label{eq:expansion}\tag{2} \end{align}\]เพราะสิ่งที่เราต้องการคือ $S_k(n)$ และตอนนี้เรามีของเพียงพอที่จะคำนวณมันได้แล้ว ซึ่งก็คือให้ $\eqref{eq:telescope} = \eqref{eq:expansion}$ แล้วจัดข้างสมการนิดหน่อยก็จะพบกับคำตอบว่า
\[S_k(n) = \frac1{k+1} \left( \sum_{p=1}^{k+1} \binom{k+1}p n^p - \sum_{p=0}^{k-1} \binom{k+1}p S_p(n) \right) \label{eq:pascal}\tag{3}\]นี่คือเทคนิคและสูตรในทำนองเดียวกันกับที่ Blaise Pascal (เจ้าของเดียวกับสามเหลี่ยมปัสกาล) ค้นพบเมื่อปี 1654 นั่นเอง ซึ่งสูตรนี้บอกเราโดยนัยว่า เมื่อต้องการคำนวณ $S_k(n)$ เราต้องหา $S_p(n)$ สำหรับทุก $p < k$ มาให้เรียบร้อยเสียก่อน
แล้วมันจะเป็นไปได้มั้ยที่จะไม่ต้องคำนวณ $S_p(n)$ อื่นๆ … สังเกตว่าจากกรณีพื้นฐานที่ $S_0(n) = n$ เราสามารถอุปนัยได้ว่าพหุนาม $S_k(n)$ นั้นมีดีกรี $k+1$ เราจะเดาว่าโครงสร้างคำตอบที่เราต้องการก็ควรจะอิงกับพจน์จาก $\sum\binom{k+1}{p}n^p$ เพียงอย่างเดียว โดยจะพยายามละลายพจน์ $\sum\binom{k+1}{p}S_p(n)$ ให้ไปหลอมรวมกับมัน ซึ่งก็คือเราอยากจัด $\eqref{eq:pascal}$ ให้กลายเป็นสูตรที่มีหน้าตาเช่นนี้
\[S_k(n) = \frac1{k+1} \left( \binom{k+1}{k+1} \boxed{?} n^{k+1} + \binom{k+1}k \boxed{?} n^k + \cdots + \binom{k+1}1 \boxed{?} n \right) \label{eq:guess}\tag{4}\]ทางหนึ่งที่สามารถทำได้ คือเราจะกระจายค่าของแต่ละพจน์ใน $\eqref{eq:pascal}$ เพื่อพยายามจัดรูปออกมาให้เป็น $\eqref{eq:guess}$ ต่อไปนี้จะขอเขียนลวกๆ โดยเอาเมทริกซ์เข้ามาช่วย ซึ่งน่าจะทำให้เราเห็นภาพได้อย่างชัดเจนว่ามันคือ
\[S_k(n) \cong \frac1{k+1} \begin{pmatrix} +\binom{k+1}{k+1} & +\binom{k+1}{k} & +\binom{k+1}{k-1} & +\binom{k+1}{k-2} & \cdots & +\binom{k+1}{1} \\ \boxed{\color{red}-\tbinom{k+1}{k-1}\times} & \boxed{S_{k-1}(n)} & \cdot & \cdot & \cdot & \cdot \\ \boxed{\color{green}-\tbinom{k+1}{k-2}\times} && \boxed{S_{k-2}(n)} & \cdot & \cdot & \cdot \\ \boxed{\color{blue}-\tbinom{k+1}{k-3}\times} &&& \boxed{S_{k-3}(n)} & \cdot & \cdot \\ \vdots &&&& \ddots & \vdots \\ \boxed{-\tbinom{k+1}0\times} &&&&& \boxed{S_0(n)} \end{pmatrix} \begin{bmatrix} n^{k+1} \\ n^k \\ n^{k-1} \\ n^{k-2} \\ \vdots \\ n \end{bmatrix}\]โดยที่กล่องซ้ายสุดในแต่ละแถวคือตัวคูณประจำแถวนั้นๆ ส่วนกล่องถัดไปด้านขวาคือ $S_p(n)$ ณ ดีกรีสูงสุดก่อนที่จะกระจายเข้าเมทริกซ์ ซึ่งคราวนี้เราจะกระจายด้วย $\eqref{eq:guess}$ แทน สนใจเฉพาะเมทริกซ์นี้ เราจะได้
\[\begin{pmatrix} +\binom{k+1}{k+1} & +\binom{k+1}{k} & +\binom{k+1}{k-1} & +\binom{k+1}{k-2} & \cdots & +\binom{k+1}{1} \\ & {\color{red}-\binom{k+1}{k-1}}\frac1k\binom{k}{k}\boxed{?} & {\color{red}-\binom{k+1}{k-1}}\frac1k\binom{k}{k-1}\boxed{?} & {\color{red}-\binom{k+1}{k-1}}\frac1k\binom{k}{k-2}\boxed{?} & \cdot & {\color{red}-\binom{k+1}{k-1}}\frac1k\binom{k}{1}\boxed{?} \\ && {\color{green}-\binom{k+1}{k-2}}\frac1{k-1}\binom{k-1}{k-1}\boxed{?} & {\color{green}-\binom{k+1}{k-2}}\frac1{k-1}\binom{k-1}{k-2}\boxed{?} & \cdot & {\color{green}-\binom{k+1}{k-2}}\frac1{k-1}\binom{k-1}{1}\boxed{?} \\ &&& {\color{blue}-\binom{k+1}{k-3}}\frac1{k-2}\binom{k-2}{k-2}\boxed{?} & \cdot & {\color{blue}-\binom{k+1}{k-3}}\frac1{k-2}\binom{k-2}{1}\boxed{?} \\ &&&& \ddots & \vdots \\ &&&&& -\binom{k+1}0\frac11\binom11\boxed{?} \end{pmatrix}\]
สังเกตว่าในแถวแนวนอนใดๆ ที่ไม่ใช่แถวบนสุด แต่ละช่องในเมทริกซ์นั้นจะขึ้นต้นด้วย $-\binom{k+1}{k-?}$ เราจะพยายามเปลี่ยนพจน์นี้ให้เหมือนกับ $+\binom{k+1}{k-?}$ ที่อยู่แถวบนสุดในคอลัมน์ของมันเอง เพื่อให้เราสามารถบวกลบช่องต่างๆ จากคอลัมน์เดียวกันได้ในภายหลัง
เช่น สำหรับพจน์ $-\binom{k+1}{k-3}\frac1{k-2}\binom{k-2}{k-2}\boxed{?}$ (แถวที่ 4 คอลัมน์ที่ 4) เราต้องการเขี่ยให้พจน์นี้ติดตัวคูณ $+\binom{k+1}{k-2}$ แทน ซึ่งอาจทำได้ผ่านเทคนิคประมาณนี้
\[\begin{align} \binom{k+1}{k-3}\frac1{k-2} &= \frac{(k+1)!}{(k-3)!4!} \frac1{k-2} \\ &= \frac{1\cdot2\cdot3\cdots(k+1)}{1\cdot2\cdots(k-3)\cdot{\color{blue}4}\cdot3\cdot2\cdot1} \frac{\color{red}(k-2)}{\color{red}(k-2)} \frac1{k-2} \\ &= \frac{1\cdot2\cdot3\cdots(k+1)}{1\cdot2\cdots(k-3)\cdot{\color{red}(k-2)}\cdot3\cdot2\cdot1} \frac{\color{red}(k-2)}{\color{blue}4} \frac1{k-2} \\ &= \frac{(k+1)!}{(k-2)!3!} \frac{(k-2)}4 \frac1{k-2} \\ &= \binom{k+1}{k-2} \frac14 \end{align}\]เมื่อไล่ทำแบบนี้จนครบทุกช่อง เมทริกซ์ดังกล่าวก็จะกลายเป็น
\[\begin{pmatrix} +\binom{k+1}{k+1} & \color{red}+\binom{k+1}{k} & \color{green}+\binom{k+1}{k-1} & \color{blue}+\binom{k+1}{k-2} & \cdots & +\binom{k+1}{1} \\ & {\color{red}-\binom{k+1}{k}}\frac12\boxed{?} & {\color{green}-\binom{k+1}{k-1}}\boxed{?} & {\color{blue}-\binom{k+1}{k-2}}\frac32\boxed{?} & \cdot & -\binom{k+1}{1}\frac12\binom{k}{1}\boxed{?} \\ && {\color{green}-\binom{k+1}{k-1}}\frac13\boxed{?} & {\color{blue}-\binom{k+1}{k-2}}\boxed{?} & \cdot & -\binom{k+1}{1}\frac13\binom{k}{2}\boxed{?} \\ &&& {\color{blue}-\binom{k+1}{k-2}}\frac14\boxed{?} & \cdot & -\binom{k+1}{1}\frac14\binom{k}{3}\boxed{?} \\ &&&& \ddots & \vdots \\ &&&&& -\binom{k+1}{1}\frac1{k+1}\binom{k}{k}\boxed{?} \end{pmatrix}\]หรือมองย้อนกลับไปที่ภาพรวมได้ว่า
\[S_k(n) \cong \frac1{k+1} \begin{pmatrix} +1 & +1 & +1 & +1 & \cdots & +1 \\ & -\frac12\binom11\boxed{?} & -\frac12\binom21\boxed{?} & -\frac12\binom31\boxed{?} & \cdot & -\frac12\binom{k}{1}\boxed{?} \\ && -\frac13\binom22\boxed{?} & -\frac13\binom32\boxed{?} & \cdot & -\frac13\binom{k}{2}\boxed{?} \\ &&& -\frac14\binom33\boxed{?} & \cdot & -\frac14\binom{k}{3}\boxed{?} \\ &&&& \ddots & \vdots \\ &&&&& -\frac1{k+1}\binom{k}{k}\boxed{?} \end{pmatrix} \begin{bmatrix} \binom{k+1}{k+1} n^{k+1} \\ \binom{k+1}{k} n^k \\ \binom{k+1}{k-1} n^{k-1} \\ \binom{k+1}{k-2} n^{k-2} \\ \vdots \\ \binom{k+1}{1} n \end{bmatrix}\]
สังเกตว่าทุกช่องที่มี $\boxed{?}$ ติดอยู่นั้นจะถูกคูณกับค่าคงที่เสมอ นั่นหมายความว่าไม่ว่าเราจะเปลี่ยนค่า $k$ เป็นเท่าไหร่ แต่ถ้าเราแทนที่ $\boxed{?}$ ณ ตำแหน่งเดิมๆ ด้วยค่าเดิมซ้ำๆ ผลรวมของแต่ละคอลัมน์ก็จะมีค่าเท่าเดิมเสมอ
และเมื่ออุปนัยลงไปก็จะพบว่าแต่ละ $\boxed{?}$ มันคือค่าเดิมซ้ำๆ เช่นนั้นจริง เราจึงเดินทางมาถึงข้อสรุปที่ว่า
\[S_k(n) \cong \frac1{k+1} \begin{pmatrix} +1 & +1 & +1 & +1 & \cdots & +1 \\ & -\frac12\binom11B_0 & -\frac12\binom21B_1 & -\frac12\binom31B_2 & \cdot & -\frac12\binom{k}{1}B_{k-1} \\ && -\frac13\binom22B_0 & -\frac13\binom32B_1 & \cdot & -\frac13\binom{k}{2}B_{k-2} \\ &&& -\frac14\binom33B_0 & \cdot & -\frac14\binom{k}{3}B_{k-3} \\ &&&& \ddots & \vdots \\ &&&&& -\frac1{k+1}\binom{k}{k}B_0 \end{pmatrix} \begin{bmatrix} \binom{k+1}{k+1} n^{k+1} \\ \binom{k+1}{k} n^k \\ \binom{k+1}{k-1} n^{k-1} \\ \binom{k+1}{k-2} n^{k-2} \\ \vdots \\ \binom{k+1}{1} n \end{bmatrix} = \frac1{k+1} \begin{bmatrix} \binom{k+1}{k+1} B_0 n^{k+1} \\ \binom{k+1}k B_1 n^k \\ \binom{k+1}{k-1} B_2 n^{k-1} \\ \binom{k+1}{k-2} B_3 n^{k-2}\\ \cdots \\ \binom{k+1}1 B_k n \end{bmatrix}\]
หรือก็คือ
\[S_k(n) = \frac1{k+1} \sum_{p=1}^{k+1} \binom{k+1}{p} B_{k+1-p} n^p \label{eq:bernoulli}\tag{5}\]โดยค่าคงที่ $B_n$ นั้นถูกเรียกว่าจำนวนแบร์นูลลี เพราะสมการและค่าคงที่นี้ถูกค้นพบและอธิบายให้อยู่ในรูปทั่วไปได้สำเร็จสำหรับทุกๆ $k$ โดย Jacob Bernoulli ผ่านงานตีพิมพ์ปี 1713 หลังจากที่เขาเสียชีวิตไปแล้ว
ซึ่งจากเมทริกซ์ที่นำไปสู่สมการ $\eqref{eq:bernoulli}$ สังเกตว่าเราสามารถคำนวณ $B_n$ ต่างๆ ที่ต้องการได้ผ่าน
\[B_n = 1 - \sum_{i=0}^{n-1} \frac1{1+i} \binom{n}{i} B_{n-i}\]ที่เราจะคำนวณหาค่าแรกๆ บางค่าออกมาได้ดังนี้
\[\begin{array}{c|ccccccccccccc} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline B_n & 1 & \frac12 & \frac16 & 0 & -\frac1{30} & 0 & \frac1{42} & 0 & -\frac1{30} & 0 & \frac5{66} & 0 & -\frac{691}{2730} \end{array}\]แม้สมการ $B_n$ จะดูเรียบง่าย แต่ก็เกี่ยวเนื่องกับการคำนวณตัวเลขขนาดใหญ่เป็นจำนวนมากในลักษณะวนลูป มันจึงไม่ค่อยเหมาะที่จะเป็นงานสำหรับมนุษย์เสียเท่าไหร่ … อันที่จริงแล้ว Ada Lovelace ผู้ซึ่งได้ชื่อว่าเป็นโปรแกรมเมอร์คนแรกของโลก ก็ได้ตีพิมพ์โปรแกรมคอมพิวเตอร์แรกของโลกสำหรับคำนวณค่าคงที่ดังกล่าวในปี 1843 อีกด้วย
อ้างอิง
- Nathaniel Larson, The Bernoulli Numbers: A Brief Primer
- Janet Beery, Sums of Powers of Positive Integers
- Roger B. Nelsen, Proofs Without Words II

author