แบบจำลองหน้าคลื่น และเพื่อนบ้านในสวนผลไม้
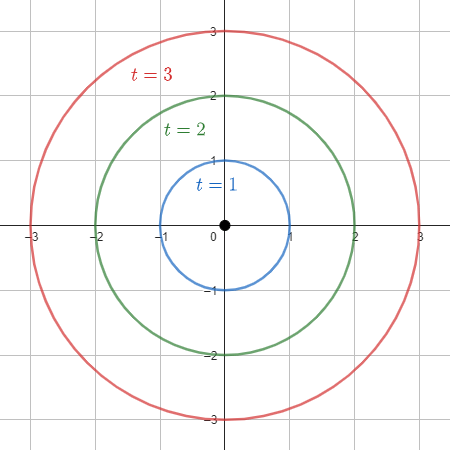
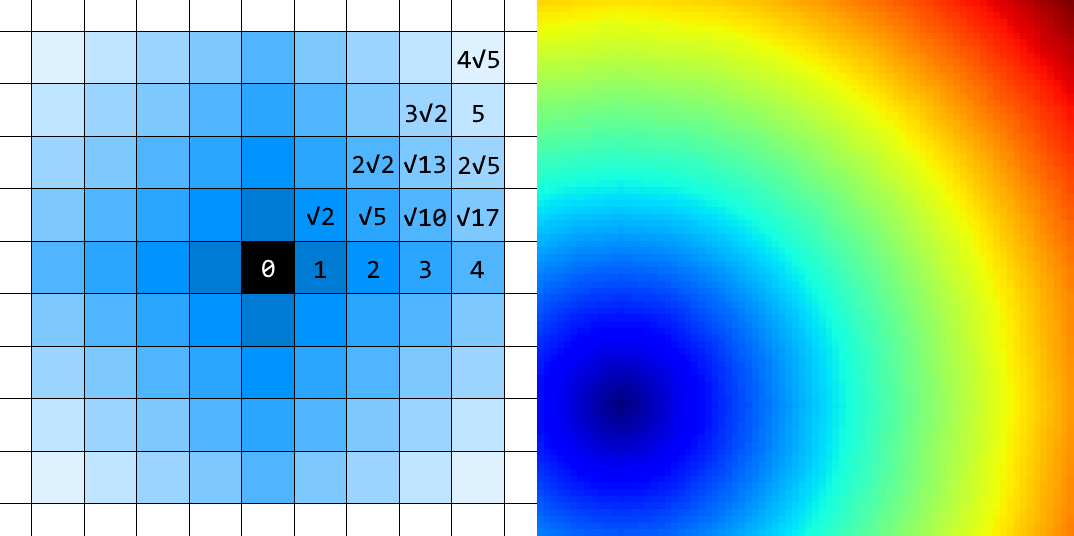
เรารู้กันดีว่าเมื่อปาก้อนหินลงไปในน้ำ จะเกิดคลื่นผิวน้ำที่มีหน้าคลื่นแผ่ขยายเป็นรูปวงกลม เพื่อความง่ายเราจะกำหนดให้คลื่นเคลื่อนที่ด้วยความเร็วคงที่ที่ $v$ เมตรต่อวินาทีไปเลย ดังนั้นเมื่อเวลาผ่านไป $t$ วินาที หน้าคลื่นก็จะมีรูปร่างเป็นวงกลมที่มีรัศมี $vt$ เมตรนั่นเอง
การวิเคราะห์โครงสร้างดังกล่าวนั้นเป็นเรื่องง่ายในทางคณิตศาสตร์ แต่ถ้าต้องเอามาเขียนเป็นโปรแกรมจำลองการเกิดคลื่นน้ำก็อาจจะปวดหัวๆ หน่อย (หรือคนอื่นไม่ปวด? เราปวดหัวอยู่คนเดียว 555555555)
วิธีที่ง่ายและถูกต้อง (ตามข้อจำกัดของโจทย์) ในการจำลองหน้าคลื่น ณ เวลาต่างๆ ที่เราที่สนใจ ก็คือการวาดวงกลมด้วยรัศมีที่คำนวณได้ข้างต้นไปเลย
วงกลมแทนหน้าคลื่น ณ เวลาต่างๆ
อย่างไรก็ตาม การวาดวงกลมง่ายๆ เช่นนี้ก็มีข้อจำกัดว่าผิวน้ำต้องราบเรียบไม่มีสิ่งใดมากีดขวาง และความเร็วของคลื่นก็ต้องเป็นค่าคงที่อีกด้วย ดังนั้นเราจึงต้องการแบบจำลองที่มีรายละเอียดมากขึ้นเพื่ออธิบายกรณีที่ซับซ้อนยิ่งกว่านั้น ซึ่งผลลัพธ์ของการหักเลี้ยวคลื่นน้ำเมื่อวิ่งไปกระทบวัตถุต่างๆ มันอาจจะไม่ได้มีโครงสร้างเรียบง่ายเป็นแค่วงกลมอีกต่อไปแล้ว
หนึ่งในแบบจำลองที่เขียนโค้ดได้ง่ายและเร็วนั้นเลียนแบบมาจากการแก้ปัญหาเขาวงกต โดยเราจะตีตารางแผนที่เป็นช่องๆ พร้อมทั้งกำหนดว่าแต่ละช่องนั้นมีเพื่อนบ้านเป็นช่องอื่นใดบ้าง แล้วใช้เทคนิคการค้นหาในแนวกว้าง (breadth-first search) มาคำนวณเส้นทางสั้นที่สุดไปยังช่องใดๆ โดยเริ่มจากจุดเริ่มต้นแล้วเดินผ่านบรรดาเพื่อนบ้านเป็นทอดๆ ซึ่งก็คือเราจะได้ว่าหน้าคลื่นเดินทางไปถึงแต่ละช่องด้วยเวลาน้อยสุดเท่าไหร่ ขั้นตอนวิธีดังกล่าวเมื่อแปลงเป็นโค้ดก็คงเขียนได้ประมาณนี้
grid = [[None for _ in range(WIDTH)] for _ in range(HEIGHT)]
queue = [(0, ROW, COL)]
while queue:
d0, r0, c0 = heappop(queue)
if grid[r0][c0] is not None:
continue
grid[r0][c0] = d0
for r1, c1 in neighbors(r0, c0):
if 0 <= r1 < HEIGHT and 0 <= c1 < WIDTH and grid[r1][c1] is None:
d1 = d0 + hypot(r1-r0, c1-c0)
heappush(queue, (d1, r1, c1))
จุดสำคัญคือฟังก์ชัน neighbors ที่เอาไว้ลิสต์ช่องเพื่อนบ้าน ที่ถ้าเราออกแบบฟังก์ชันนี้มาไม่ดี ผลลัพธ์แบบจำลองของเราก็จะมีหน้าตาผิดจากความเป็นจริงไปไกลเลย
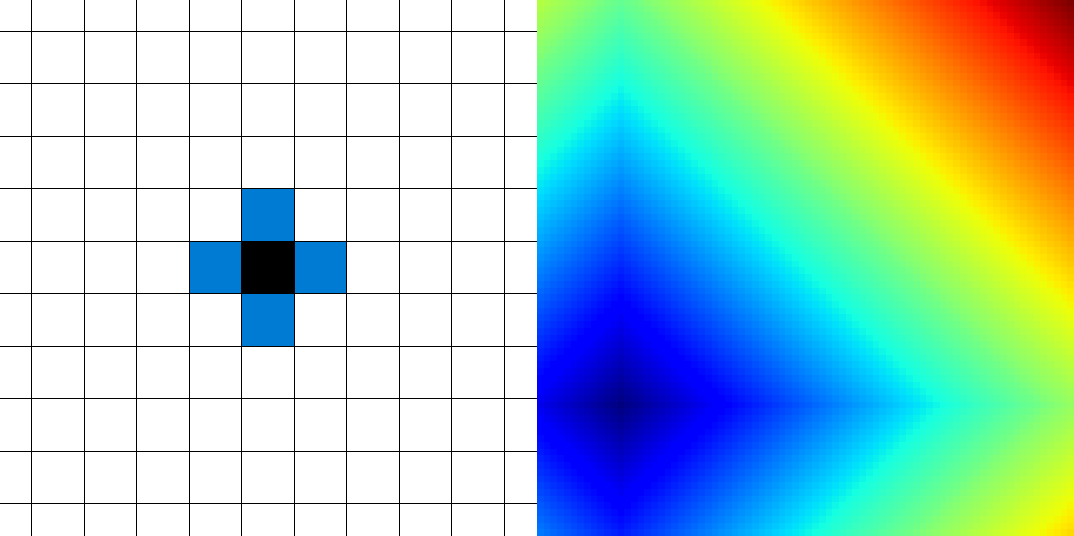
อย่างเช่นเมื่อเราให้เพื่อนบ้านมีแค่สี่ทิศ ขึ้น-ลง-ซ้าย-ขวา ตามโค้ดตัวอย่างต่อไปนี้
def neighbors(r, c):
return ((r+dr, c+dc) for dr, dc in [(+1,0),(0,+1),(-1,0),(0,-1)])
ผลลัพธ์ที่ได้จะกลายเป็นคลื่นสี่เหลี่ยมไปซะหนิ (ซึ่งก็คือเราจะได้ระบบที่อยู่บนระยะทางแบบ $L^1$ มาแทน)
เพื่อนบ้านสี่ทิศที่ก่อให้เกิดหน้าคลื่นสี่เหลี่ยม
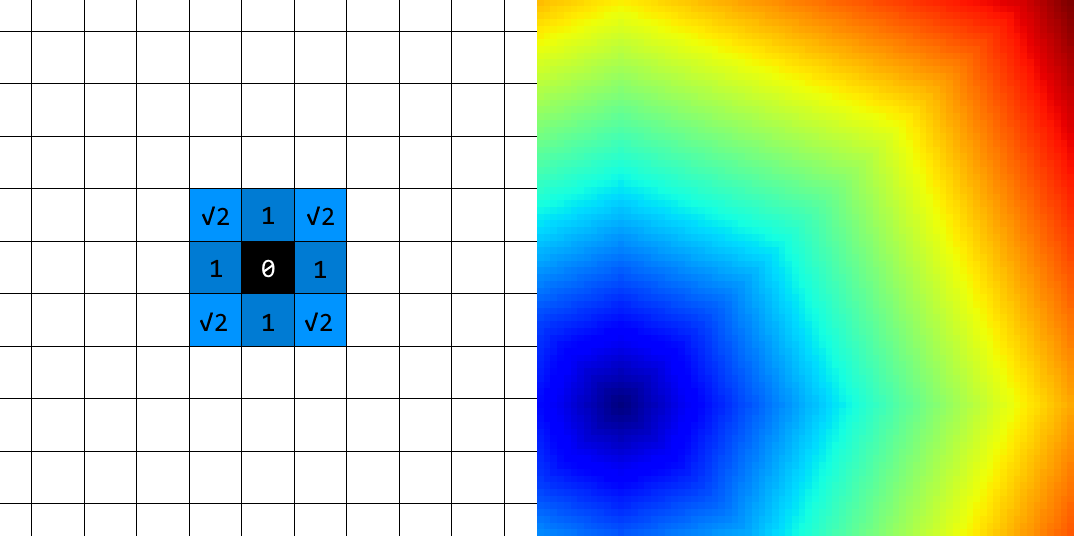
ตอนแรกก็คิดว่า งั้นก็นับเพิ่มเพื่อนบ้านที่อยู่ในแนวทะแยงมุมด้วยสิ คือใช้แปดช่องที่อยู่ติดกันก็น่าจะพอ (โดยให้ช่องที่อยู่แนวทะแยงมุมมีค่าน้ำหนักระยะห่างไกลกว่าช่องที่อยู่ติดกันในแนวขนาน)
from itertools import product
def neighbors(r, c):
return ((r+dr, c+dc) for dr, dc in product([-1,0,1],[-1,0,1]))
แต่ผลลัพธ์มันก็ยังออกมาหน้าตาประหลาด กลายเป็นได้รูปแปดเหลี่ยมด้านเท่าอยู่ดี!
เพื่อนบ้านแปดทิศที่มีระยะห่างจากจุดศูนย์กลางไม่เท่ากัน ก่อให้เกิดหน้าคลื่นเป็นรูปแปดเหลี่ยม
หยุดคิดซักหน่อยจะพอเห็นว่า ความคลาดเคลื่อนมันเกิดจากการที่เราไม่สามารถเดินตรงๆ ด้วยมุมที่ถูกต้องไปยังช่องเป้าหมายได้ในทันที แต่เราต้องเดินอ้อมๆ เพื่อประกอบสร้างมุมที่เราต้องการจากมุมของเพื่อนบ้านที่เรามีอย่างจำกัดเท่านั้น
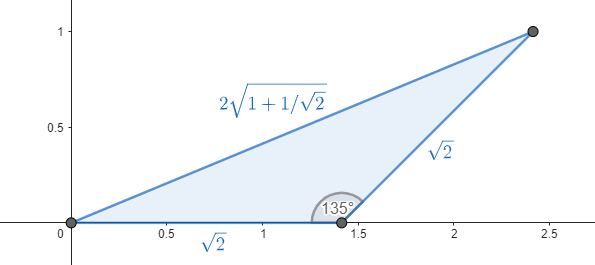
อย่างเช่นในระบบเพื่อนบ้านแปดทิศ เราจะมีมุมที่สำคัญให้ใช้ได้แค่สองมุมเท่านั้น ซึ่งก็คือมุม $0^\circ$ และมุม $45^\circ$ (มุมอื่นๆ เกิดจากการกลับด้าน/ตั้งฉากของสองมุมพื้นฐานนี้) ซึ่งเราสามารถเขียนสองมุมนี้ในอีกทางได้ว่าเป็นเวกเตอร์ $(\begin{smallmatrix}1\newline0\end{smallmatrix})$ กับ $(\begin{smallmatrix}1\newline1\end{smallmatrix})$ ดังนั้นหากเป้าหมายที่เราต้องการอยู่ที่มุม $\theta = \atan\frac{y}{x}$ เราก็ต้องสร้าง $(\begin{smallmatrix}x \newline y\end{smallmatrix})$ กลับขึ้นมาจากเวกเตอร์พื้นฐานสองตัวนั้น เช่น เมื่อเราต้องการมุม $36.87^\circ$ จะได้ $(\begin{smallmatrix}4\newline3\end{smallmatrix})=(\begin{smallmatrix}1\newline0\end{smallmatrix})+3(\begin{smallmatrix}1\newline1\end{smallmatrix})$ หรือก็คือเราต้องเดินขนานที่มุม $0^\circ$ หนึ่งครั้ง แล้วเดินเฉียงที่มุม $45^\circ$ อีกสามครั้งนั่นเอง
ในระบบเพื่อนบ้านแปดทิศ ความคลาดเคลื่อนมากสุดคือช่องที่เป็นพหุคูณของ $(1{+}\sqrt2,1)$ หรือก็คือทุกครั้งที่เดินเฉียงหนึ่งครั้งจะต้องเดินขนาน $\sqrt2$ ครั้ง ซึ่งกินระยะทางมากกว่าการเดินตรงๆ ประมาณ $8.24\%$
ถ้ายังจะดั้นด้นสร้างแบบจำลองในแนวทางนี้ต่อไป หนทางแก้ปัญหาความคลาดเคลื่อนของระยะทางในมุมที่ไม่รู้จัก คงหนีไม่พ้นการขยายละแวกเพื่อนบ้านให้มีขนาดใหญ่ขึ้น (เพิ่มมุมพื้นฐานให้เยอะขึ้น) คือจากการใช้เพื้อนบ้านแค่ $3{\times}3$ (เพื่อนบ้านแปดทิศ) ก็อาจจะต้องเปลี่ยนไปใช้ $5{\times}5$ หรือ $7{\times}7$ (หรือใหญ่ยิ่งกว่า)
ตัวอย่างผลลัพธ์เมื่อใช้เพื่อนบ้าน $9{\times}9$ ซึ่งก็ดูเนียนดี แต่ก็แลกมากับการคำนวณที่ช้ากว่ากันหลายเท่าตัว
แม้ว่าแบบจำลองนี้จะจำลองระยะทางแบบ $L^2$ ได้แม่นยำขึ้นเรื่อยๆ แต่ยิ่งเราขยายขนาดละแวกเพื่อนบ้านเป็น $(2n{+}1)\times(2n{+}1)$ ช่อง ก็แปลว่าเรามีจำนวนช่องทั้งหมดใน queue ที่ต้องพิจารณาโตตามเป็น $O(n^2)$ ด้วย ซึ่งจะส่งผลให้อัลกอริทึมของเราทำงานได้ช้าลงนั่นเอง
ถ้าเช่นนั้นแล้วเราสามารถทำให้มันดีขึ้นได้หรือเปล่า? สังเกตว่าเพื่อนบ้านบางตัวที่เราใส่เข้าไปใน queue นั้น มันจะถูกใส่ลง queue ซ้ำในรอบที่เราพิจารณาช่องอื่นอยู่ดี เราจึงไม่มีความจำเป็นที่จะต้องรีบใส่เพื่อนบ้านบางตัวลงใน queue ก็ได้ เช่น จากช่อง $(0,0)$ เราไม่จำเป็นต้องใส่เพื่อนบ้าน $(7,0)$ ตั้งแต่แรก ขอแค่ในรอบนี้เราใส่เพื่อนบ้าน $(1,0)$ เข้าไปก็เพียงพอ แล้วหลังจากนั้นในรอบของ $(1,0)$ ก็จะใส่เพื่อนบ้าน $(2,0)$ มาเอง และเมื่อพิจารณาไล่รอบถัดไปเรื่อยๆ สุดท้ายจะเห็นว่า $(7,0)$ ถูกใส่เข้ามาเองในที่สุด
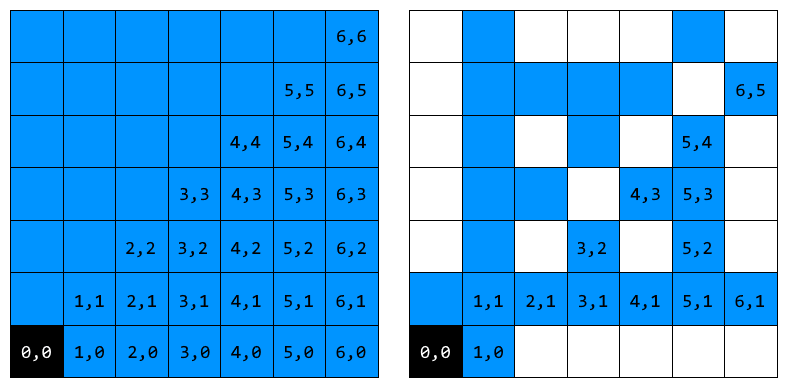
ซีกขวาบนของละแวก $13{\times}13$: (ซ้าย) เพื่อนบ้านทุกช่อง, (ขวา) แค่เพื่อนบ้านที่เป็นจำนวนเฉพาะสัมพัทธ์
นั่นก็คือเมื่อเราจะเพิ่มเพื่อนบ้านลงใน queue เราไม่จำเป็นต้องพิจารณาเพื่อนบ้านที่เป็นพหุคูณของเพื่อนบ้านตัวที่ใกล้กว่าอีกแล้ว หรือพูดอีกอย่างได้ว่า เมื่อเรามีเพื่อนบ้าน $(x,y)$ อยู่ก่อนหน้า เราไม่จำเป็นต้องมองว่า $(mx,my)$ ที่ $m>1$ เป็นเพื่อนบ้านอีกต่อไป
เงื่อนไขของการเลือกคบเพื่อนบ้านเช่นนี้ก็คือแนวคิดของจำนวนเฉพาะสัมพัทธ์นั่นเอง ซึ่งเราจะรู้ได้ว่าควรคบใครเป็นเพื่อนบ้านบ้างผ่านการทดสอบว่าตัวหารร่วมมากมีค่าเท่ากับหนึ่งหรือไม่ จึงทำให้ได้โค้ดนี้ออกมา
from math import gcd
def neighbors(r, c, size=3):
assert size % 2 == 1 and size > 1
vs = [v - size//2 for v in range(size)]
return ((r+dr, c+dc) for dr, dc in product(vs, vs) if gcd(dr, dc) == 1)
แน่นอนว่าโค้ดนี้เร็วขึ้นทางปฏิบัติ เพราะเราสามารถบีบให้ queue มีขนาดเล็กลงได้จริง (และการเช็ค gcd นั้นก็ถูกมากๆ จนอาจจะมองว่าฟรีได้เลย)
อย่างไรก็ตาม สังเกตว่าการเลือกเพื่อนบ้าน $(2n{+}1)\times(2n{+}1)$ ที่ใหญ่ขึ้น บางครั้งก็ช่วยให้ประหยัดได้เยอะ เช่นที่ $n=6$ เราจะมีเพื่อนบ้านใหม่ในชั้นนอกสุดแค่สองตัว คือ $(1,6)$ กับ $(5,6)$ แต่พอขยายไปที่ $n=7$ กลับไม่ช่วยประหยัดแล้ว เพราะเราจะมีเพื่อนบ้านใหม่ถึงหกตัว (ไล่จาก $(1,7)$ ไปจนถึง $(6,7)$ เลย)
เราจะเรียกฟังก์ชัน $\varphi$ ซึ่งทำหน้าที่นับจำนวนเพื่อนบ้านตัวใหม่ในชั้นนอกสุดว่าฟังก์ชันทอเทียนต์ (ของ Euler) โดยหนึ่งในนิยามของมันนั้นก็เขียนได้อย่างตรงไปตรงมาว่า
\[\varphi(n) = \sum_{k=1}^n \text{coprime}(k,n)\]ซึ่งใช้งานยาก แต่มีสมบัติที่น่าสนใจคือ
\[\begin{align} \varphi(p^k) &= (p-1)p^{k-1}, && \text{$p$ is prime} \\ \varphi(ab) &= \varphi(a) \cdot \varphi(b), && \text{$\gcd(a,b) = 1$} \end{align}\]หรือลดรูปสรุปได้ว่า
\[\varphi(n) = n \prod_{p|n} \left( 1 - \frac1p \right)\]เนื่องจากเราไม่ได้สนใจแค่เพื่อนบ้านในชั้นสุดท้าย แต่สนใจเพื่อนบ้านทั้งหมดตั้งแต่ชั้นแรกไล่ออกมา เราจะเปลี่ยนไปสนใจฟังก์ชันรวมยอดทอเทียนต์แทน ซึ่งก็คือ
\[\Phi(n) = \sum_{k=1}^n \varphi(k)\]สังเกตว่า $\Phi(n)$ สนใจนับแค่เพื่อนบ้านในละแวกแบบสามเหลี่ยม (สนใจเฉพาะ $(x,y)$ ที่ $x \le y$ เท่านั้น) สำหรับละแวกแบบสี่เหลี่ยมจะนับได้มากขึ้นเป็นสองเท่า นั่นก็คือเราต้องการคำนวณหาค่า
\[\frac{2\Phi(n)}{n^2} = ?\]ซึ่งก็คือสัดส่วนของเพื่อนบ้านคนสำคัญต่อเพื่อนบ้านทั้งหมดในละแวกที่เราตีกรอบไว้นั่นเอง
โชคร้ายหน่อยที่ฟังก์ชันนี้ไม่มีวิธีลดรูปดีๆ ให้คำนวณได้ง่ายแล้ว (หรือมีแต่เราไม่รู้เอง 5555) ทางแรกที่เราพอจะทำได้ก็คือสนใจเฉพาะกรณี $n\to\infty$ ไปเลย (แล้วหวังว่ามันจะลู่เข้าเร็วพอจนทำให้เราประมาณค่าที่ $n$ อื่นๆ ว่าได้ผลลัพธ์ใกล้เคียงกัน)
ส่วนอีกทางคือเราจะตีความ $2\Phi(n)/n^2$ ใหม่ว่ามันคือความน่าจะเป็นที่จะเจอจำนวนเฉพาะสัมพัทธ์ เมื่อเราสุ่มหยิบจำนวนเต็มใดๆ มาสองตัวนั่นเอง (กลับไปอ้างอิงนิยามแรกของ $\varphi$)
ซึ่งการที่จำนวนเต็มสองจำนวนจะเป็นจำนวนเฉพาะสัมพัทธ์ต่อกันได้ หมายความว่าสำหรับจำนวนเฉพาะแต่ละตัว จำนวนเฉพาะตัวนั้นจะต้องหารไม่ลงตัวกับจำนวนสุ่มทั้งสองตัวพร้อมกัน
สนใจจำนวนเฉพาะ $p$ ใดๆ จะเห็นว่าความน่าจะเป็นที่
- จำนวนสุ่มตัวเดียวถูก $p$ หารลงตัวคือ $1/p$
- จำนวนสุ่มสองตัวถูก $p$ หารลงตัวพร้อมกันคือ $1/p^2$
- จำนวนสุ่มสองตัวไม่ถูก $p$ หารลงตัวพร้อมกันคือ $(1-1/p^2)$
ดังนั้นจึงได้ว่าความน่าจะเป็นที่จำนวนเต็มสองจำนวนจะเป็นจำนวนเฉพาะสัมพัทธ์ต่อกันก็คือ
\[\begin{align*} \lim_{n\to\infty} \frac{2\Phi(n)}{n^2} &= \prod_p \left( 1 - \frac1{p^2} \right) \\ &= \left( 1 - \frac1{2^2} \right)\!\! \left( 1 - \frac1{3^2} \right)\!\! \left( 1 - \frac1{5^2} \right)\!\! \left( 1 - \frac1{7^2} \right)\!\! \left( 1 - \frac1{11^2} \right)\!\! \left( 1 - \frac1{13^2} \right) \cdots \end{align*}\]ความเศร้าก็คือเราวนกลับมาเจออะไรที่คำนวณยากอีกแล้ว1 เพราะนอกจาก $\prod_p(1-1/p^2)$ จะเป็นผลคูณอนันต์พจน์ไม่พอ แต่ละพจน์ยังอิงอยู่บนจำนวนเฉพาะที่ค่าโดดไปโดดมาอีกด้วย …
ถึงตอนนี้จะขอเปลี่ยนไปสนใจฟังก์ชันซีตาของ Reimann ซักนิด ซึ่งมันเป็นผลบวกอนันต์พจน์ที่มีนิยามว่า
\[\zeta(s) = \sum_{k=1}^\infty \frac1{k^s} = \frac1{1^s} + \frac1{2^s} + \frac1{3^s} + \cdots\]สังเกตว่า
\[\begin{align*} \zeta(s) &= \frac1{1^s} + \frac1{2^s} + \frac1{3^s} + \frac1{4^s} + \frac1{5^s} + \cdots \\ \left( \frac1{2^s} \right)\; \zeta(s) &= \frac1{2^s} + \frac1{4^s} + \frac1{6^s} + \frac1{8^s} + \frac1{10^s} + \cdots \\ \left( 1 - \frac1{2^s} \right)\; \zeta(s) &= \frac1{1^s} + \frac1{3^s} + \frac1{5^s} + \frac1{7^s} + \frac1{9^s} + \cdots \\ \left( \frac1{3^s} \right)\!\! \left( 1 - \frac1{2^s} \right)\; \zeta(s) &= \frac1{3^s} + \frac1{9^s} + \frac1{15^s} + \frac1{21^s} + \frac1{27^s} + \cdots \\ \left( 1 - \frac1{3^s} \right)\!\! \left( 1 - \frac1{2^s} \right)\; \zeta(s) &= \frac1{1^s} + \frac1{5^s} + \frac1{7^s} + \frac1{11^s} + \frac1{13^s} + \cdots \\ \left( \frac1{5^s} \right)\!\! \left( 1 - \frac1{3^s} \right)\!\! \left( 1 - \frac1{2^s} \right)\; \zeta(s) &= \frac1{5^s} + \frac1{25^s} + \frac1{35^s} + \frac1{55^s} + \frac1{65^s} + \cdots \\ \left( 1 - \frac1{5^s} \right)\!\! \left( 1 - \frac1{3^s} \right)\!\! \left( 1 - \frac1{2^s} \right)\; \zeta(s) &= \frac1{1^s} + \frac1{7^s} + \frac1{11^s} + \frac1{13^s} + \frac1{17^s} + \cdots \end{align*}\]พูดอีกอย่างก็คือเรากำลังร่อนตะแกรงของ Eratosthenes อยู่นั่นเอง โดยความปราดเปรื่องอันเป็นหัวใจสำคัญของวิธีนี้อยู่ตรงความพิถีพิถันในการลบจำนวนประกอบทิ้งออกไปในแต่ละรอบ ซึ่งก็คือเราจะลบแต่ละ $1/k^s$ เพียงแค่หนึ่งครั้งเท่านั้นไม่ขาดไม่เกิน ทำให้ได้ว่าในที่สุดแล้ว
\[\cdots \left( 1 - \frac1{13^s} \right)\!\! \left( 1 - \frac1{11^s} \right)\!\! \left( 1 - \frac1{7^s} \right)\!\! \left( 1 - \frac1{5^s} \right)\!\! \left( 1 - \frac1{3^s} \right)\!\! \left( 1 - \frac1{2^s} \right)\; \zeta(s) = 1\]ดังนั้น
\[\prod_p \left( 1 - \frac1{p^s} \right) = \frac1{\zeta(s)}\]หรือสำหรับข้อนี้ที่เราต้องคำนวณโอกาสที่ตัวเลขสุ่มสองตัวจะเป็นจำนวนเฉพาะสัมพัทธ์ (สนใจ $s=2$)
\[\lim_{n\to\infty} \frac{2\Phi(n)}{n^2} = \prod_p \left( 1 - \frac1{p^2} \right) = \frac1{\zeta(2)}\]ถึงตรงนี้เราก็วนกลับมาเจอคำถามที่ว่า $\zeta(2)$ นั้นมีค่าเป็นเท่าไหร่กันหละ? มันจะคำนวณได้ยากเหมือนบรรดาคำถามก่อนหน้าหรือเปล่า? เพราะอย่างไรเสียมันก็ยังเป็นผลบวกอนันต์พจน์อยู่ดี
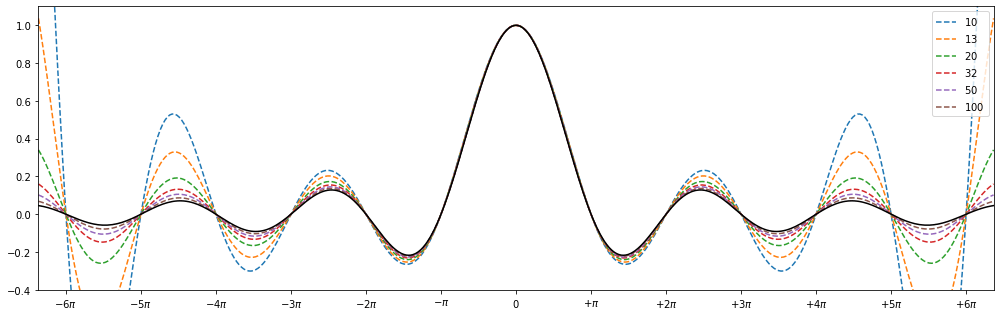
แน่นอนว่าดูผ่านๆ แล้วอาจน่ากลัว แต่อันที่จริงมันกลับหาค่าได้ง่ายมาก2 โดยเราจะเริ่มจากฟังก์ชัน $\text{sinc}$ ที่มีสมบัติประหลาดคล้ายจะเป็นฟังก์ชันคาบ (แบบฟังก์ชัน $\sin$) ซึ่งก็คือมันมีรากเป็นจำนวนอนันต์ตัว โดยรากแต่ละคู่ที่อยู่ติดกันจะเว้นระยะห่างเท่าๆ กันตลอด ยกเว้นเมื่อ $x=0$ ที่ไม่มีรากซะงั้น
การย้อนประมาณฟังก์ชัน $\text{sinc}$ จากราก โดยทดลองใช้จำนวนรากจากน้อยไปมาก จะเห็นว่ามันแม่นยำในบริเวณราก และคลาดเคลื่อนเมื่ออยู่กลางระหว่างคู่ของราก
จุดสำคัญคือเราสามารถเอารากทุกค่ามาประกอบร่างสร้างย้อนกลับเป็นฟังก์ชันนี้ได้ (ทฤษฎีบทตัวประกอบของ Weierstrass – แนวคิดทำนองเดียวกับการแยกตัวประกอบพหุนามนั่นเอง) ซึ่งเราจะได้ว่า
\[\begin{align*} \frac{\sin x}x &= \left( 1 - \frac{x}\pi \right)\!\! \left( 1 + \frac{x}\pi \right)\!\! \left( 1 - \frac{x}{2\pi} \right)\!\! \left( 1 + \frac{x}{2\pi} \right)\!\! \left( 1 - \frac{x}{3\pi} \right)\!\! \left( 1 + \frac{x}{3\pi} \right) \cdots \\ &= \left( 1 - \frac{x^2}{\pi^2} \right)\!\! \left( 1 - \frac{x^2}{4\pi^2} \right)\!\! \left( 1 - \frac{x^2}{9\pi^2} \right)\!\! \left( 1 - \frac{x^2}{16\pi^2} \right) \cdots \end{align*}\]เราจะถึกคูณกระจายวงเล็บอันมากมายจำนวนเป็นอนันต์เหล่านั้น อย่างไรก็ดี เราสามารถเลือกสนใจแค่พจน์ที่มี $x^2$ ติดอยู่ก็เพียงพอ (เทคนิคในทำนองเดียวกันกับฟังก์ชันก่อกำเนิดนั่นเอง) และทำให้ได้
\[[x^2]\frac{\sin x}x = -\left( \frac1{\pi^2} + \frac1{4\pi^2} + \frac1{9\pi^2} + \frac1{16\pi^2} + \cdots \right)\]อย่างไรก็ตาม อย่าลืมว่าเราสามารถกระจายฟังก์ชันนี้ได้อีกทางผ่านอนุกรม Taylor ที่เรารัก ซึ่งก็คือ
\[\begin{align*} \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \frac{x^{11}}{11!} + \cdots \\ \frac{\sin x}x &= 1 - \frac{x^2}{3!} + \frac{x^4}{5!} - \frac{x^6}{7!} + \frac{x^8}{9!} - \frac{x^{10}}{11!} + \cdots \end{align*}\]จึงทำให้ได้
\[[x^2]\frac{\sin x}x = -\frac1{3!} = -\frac{\zeta(2)}{\pi^2}\]และทำให้เราเดินทางมาถึงข้อสรุปเสียทีว่า
\[\lim_{n\to\infty} \frac{2\Phi(n)}{n^2} = \prod_p \left( 1 - \frac1{p^2} \right) = \frac1{\zeta(2)} = \frac6{\pi^2}\]อ้าว … อยู่ดีๆ ก็มีค่า $\pi$ โผล่เข้ามาในคำตอบเฉยเลย 🥧🥐🥗
ดังนั้นสัดส่วนของเพื่อนบ้านคนสำคัญต่อเพื่อนบ้านทั้งหมดในระนาบก็คือ $6/\pi^2 \approx 60.79\%$ ซึ่งเป็นคำตอบเดียวกันกับสวนผลไม้ของ Euclid (และปัญหา Basel) ที่ถามอ้อมๆ ถึงความน่าจะเป็นของการสุ่มเจอจำนวนเฉพาะสัมพัทธ์นั่นเอง
นั่นหมายความว่าในทางปฏิบัติแม้โค้ดข้างต้นจะเร็วขึ้นจริง แต่ทางทฤษฎีแล้วก็ยังติดขีดจำกัดที่โยนเพื่อนบ้านทิ้งได้ไม่เยอะเท่าที่หวัง สุดท้ายแล้วความซับซ้อนของจำนวนเพื่อนบ้านก็ยังคงเป็น $O(n^2)$ เช่นเดิม
อ้างอิง

author