พิจารณาทรงกลมใน $n$ มิติ ($(n{-}1)$-ทรงกลม) ที่เรายังไม่รู้จุดศูนย์กลางหรือขนาดรัศมี อย่างไรก็ตามหากเราสุ่มตัวอย่างจุดซึ่งอยู่บนขอบทรงกลมมา $n+1$ จุด เราก็จะสามารถคำนวณย้อนกลับไปหาข้อมูลต่างๆ เกี่ยวกับทรงกลมนั้นได้ โดยระบบสมการของทรงกลมในมิติ $n$ นี้ก็คือ

\[(a_{k1}-x_1)^2 + (a_{k2}-x_2)^2 + \cdots + (a_{kn}-x_n)^2 = r^2 \tag{1} \label{eq:sphere}\]

เมื่อจุดต่างๆ ที่อยู่บนขอบทรงกลมได้แก่ $p_k = (a_{k1},a_{k2},\dots,a_{kn})$ สำหรับ $0\le k\le n$ ซึ่งจะทำให้เราได้จุดศูนย์กลางทรงกลมที่ตำแหน่ง $f=(x_1,x_2,\dots,x_n)$ และรัศมีความยาวเท่ากับ $r$

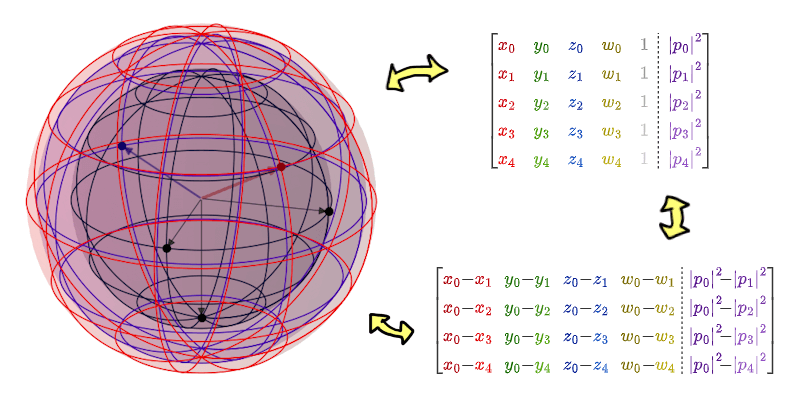
ตัวอย่างทรงกลมใน 4 มิติ และการตีความข้อมูลด้วยเมทริกซ์ที่แตกต่างกัน

แน่นอนว่าเราต้องการแก้ระบบสมการ $\eqref{eq:sphere}$ เพื่อหาจุดศูนย์กลางและรัศมีของทรงกลม แต่ตอนนี้เรายังทำงานกับระบบสมการดังกล่าวได้ยากหน่อย เพราะตัวแปร $x_i$ แต่ละตัวนั้นติดแนบแน่นอยู่กับข้อมูลภายใต้วงเล็บกำลังสอง ดังนั้นเราจะกระจายมันออกมาเป็น

\[\begin{align} (a_{k1}^2 - 2a_{k1}x_1 + x_1^2) + \cdots + (a_{kn}^2 - 2a_{kn}x_n + x_n^2) &= \\ (a_{k1}^2 + \cdots + a_{kn}^2) - 2(a_{k1}x_1 + \cdots + a_{kn}x_n) + (x_1 + \cdots + x_n)^2 &= \\ \abs{p_k}^2 - 2(a_{k1}x_1 + \cdots + a_{kn}x_n) + \abs{f}^2 &= r^2 \end{align}\]

หรือก็คือ

\[2a_{k1}x_1 + 2a_{k2}x_2 + \cdots + 2a_{kn}x_n + (r^2{-}\abs{f}^2) = \abs{p_k}^2 \tag{2} \label{eq:row}\]

นี่หมายความว่าเราสามารถมองพจน์ $(r^2{-}\abs{f}^2)$ ให้กลายเป็นตัวแปรตัวเดียวได้ และทำให้ $\eqref{eq:row}$ กลายเป็นสมการเชิงเส้น $n+1$ ตัวแปรไปในทันที! ส่งผลให้เราได้เมทริกซ์

\[\begin{bmatrix} a_{01} & a_{02} & \cdots & a_{0n} & 1 \\ a_{11} & a_{12} & & a_{1n} & 1 \\ \vdots & & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} & 1 \end{bmatrix} \begin{bmatrix} 2x_1 \\ \vdots \\ 2x_n \\ r^2{-}\abs{f}^2 \end{bmatrix} = \begin{bmatrix} \abs{p_0}^2 \\ \abs{p_1}^2 \\ \vdots \\ \abs{p_n}^2 \end{bmatrix}\]

ถึงตรงนี้ก็ง่ายแล้ว เพราะจากกฎของ Cramer ก็จะทำให้เราได้พิกัดต่างๆ ออกมาว่า

\[2x_i = \frac{ \det\begin{bmatrix} a_{01} & \cdots & a_{0,i-1} & \abs{p_0}^2 & a_{0,i+1} & \cdots & a_{0n} & 1 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n1} & \cdots & a_{n,i-1} & \abs{p_n}^2 & a_{n,i+1} & \cdots & a_{nn} & 1 \end{bmatrix} }{ \det\begin{bmatrix} a_{01} & \cdots & a_{0n} & 1 \\ \vdots & \ddots & \vdots & \vdots \\ a_{n1} & \cdots & a_{nn} & 1 \end{bmatrix} } \tag{3} \label{eq:full-det}\]

ส่วนการหารัศมีก็ทำได้ในทำนองเดียวกัน เพียงแค่เปลี่ยนหลักสุดท้ายของเมทริกซ์ที่มีแต่เลขหนึ่ง ให้กลายเป็นเวกเตอร์ $[\abs{p_1}^2,\dots,\abs{p_n}^2]$ แทนนั่นเอง

อย่างไรก็ตาม วิธีการข้างต้นมีจุดที่เรารู้สึกแปลกๆ ตอนคำนวณค่ารัศมี $r$ ที่รายละเอียดของดีเทอร์มิแนนต์มันแตกต่างจากตอนคำนวณตำแหน่ง $x_i$ ไปไกลเลย และในทางปฏิบัติ หลังจากคำนวณแต่ละ $x_i$ จนได้ตำแหน่ง $f$ มาแล้ว เราก็ไม่จำเป็นต้องใช้ดีเทอร์มิแนนต์เพื่อแก้หา $r$ อีกต่อไป เพียงแค่ใช้พีทาโกรัสก็เพียงพอ

ดังนั้นเราอาจมองปัญหานี้ใหม่ว่า เราแค่ต้องการหาจุดศูนย์กลางของทรงกลมก็พอ ซึ่งก็คือเราจะลดขนาดสมการให้เหลือเพียง $n$ ตัวแปรแทน โดยเราจะเริ่มจากการกลับไปดูระบบสมการ $\eqref{eq:row}$ ที่จะเห็นว่าทุกสมการย่อยๆ ในแต่ละแถวนั้นใช้ตัวแปร $(r^2{-}\abs{f}^2)$ เหมือนกันทั้งหมด ดังนั้นเราจะหยิบแถวของ $p_0$ มาเป็นตัวตั้ง แล้วเอาไปลบกับแถวอื่นๆ ที่เหลือ จึงทำให้ได้ระบบสมการนี้ออกมาแทน

\[2(a_{01}{-}a_{k1})x_1 + 2(a_{02}{-}a_{k2})x_2 + \cdots + 2(a_{0n}{-}a_{kn})x_n = \abs{p_0}^2{-}\abs{p_k}^2\]

หรือเขียนในรูปเมทริกซ์ได้ว่า

\[\begin{bmatrix} a_{01}{-}a_{11} & a_{02}{-}a_{12} & \cdots & a_{0n}{-}a_{1n} \\ a_{01}{-}a_{21} & a_{02}{-}a_{22} & & a_{0n}{-}a_{2n} \\ \vdots & & \ddots & \vdots \\ a_{01}{-}a_{n1} & a_{02}{-}a_{n2} & \cdots & a_{0n}{-}a_{nn} \\ \end{bmatrix} \begin{bmatrix} 2x_1 \\ 2x_2 \\ \vdots \\ 2x_n \end{bmatrix} = \begin{bmatrix} \abs{p_0}^2{-}\abs{p_1}^2 \\ \abs{p_0}^2{-}\abs{p_2}^2 \\ \vdots \\ \abs{p_0}^2{-}\abs{p_n}^2 \end{bmatrix}\]

ซึ่งทำให้ได้คำตอบพิกัดต่างๆ ดังนี้

\[2x_i = \frac{ \det\begin{bmatrix} a_{01}{-}a_{11} & \cdots & a_{0,i-1}{-}a_{1,i-1} & \abs{p_0}^2{-}\abs{p_1}^2 & a_{0,i+1}{-}a_{1,i+1} & \cdots & a_{0n}{-}a_{1n} \\ \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{01}{-}a_{n1} & \cdots & a_{0,i-1}{-}a_{n,i-1} & \abs{p_0}^2{-}\abs{p_n}^2 & a_{0,i+1}{-}a_{n,i+1} & \cdots & a_{0n}{-}a_{nn} \\ \end{bmatrix} }{ \det\begin{bmatrix} a_{01}{-}a_{11} & \cdots & a_{0n}{-}a_{1n} \\ \vdots & \ddots & \vdots \\ a_{01}{-}a_{n1} & \cdots & a_{0n}{-}a_{nn} \\ \end{bmatrix} } \tag{4} \label{eq:sub-det}\]

แม้ว่าสมการ $\eqref{eq:full-det}$ กับ $\eqref{eq:sub-det}$ ที่เป็นการหารกันของดีเทอร์มิแนนต์จะมีรายละเอียดภายในดีเทอร์มิแนนต์ที่ไม่เหมือนกันเลยก็ตาม แต่คำตอบทั้งสองสมการของมันต้องออกมาเท่ากันแน่ๆ ถ้าเราสนใจเพียงแค่ดีเทอร์มิแนนต์ที่เป็นตัวส่วนจากทั้งสองสมการ เราอาจเดาได้ว่ามันควรจะมีค่าเท่ากัน (หรือไม่งั้นก็อาจติดตัวคูณอะไรซักอย่างที่ตัดกับฝั่งตัวเศษได้พอดี เช่นตัวคูณ $-1$) ดังนั้นเราจะตั้งข้อคาดการณ์ว่า

ข้อคาดการณ์ 1: ให้เวกเตอร์ $\color{red}\vec{u}$ และเมทริกซ์ $M=[\vec{v}_1,\cdots,\vec{v}_n]$ เราจะได้

\[\det\left[\begin{array}{cccc:c} \color{red}u_1 & \color{red}u_2 & \color{red}\cdots & \color{red}u_n & 1 \\ \hdashline v_{11} & v_{12} & \cdots & v_{1n} & 1 \\ v_{21} & v_{22} & & v_{2n} & 1 \\ \vdots & & \ddots & \vdots & \vdots \\ v_{n1} & v_{n2} & \cdots & v_{nn} & 1 \end{array}\right] = \det\begin{bmatrix} {\color{red}u_1}{-}v_{11} & {\color{red}u_2}{-}v_{12} & \cdots & {\color{red}u_n}{-}v_{1n} \\ {\color{red}u_1}{-}v_{21} & {\color{red}u_2}{-}v_{22} & & {\color{red}u_n}{-}v_{2n} \\ \vdots & & \ddots & \vdots \\ {\color{red}u_1}{-}v_{n1} & {\color{red}u_2}{-}v_{n2} & \cdots & {\color{red}u_n}{-}v_{nn} \\ \end{bmatrix}\]

การจะพิสูจน์ว่าข้อคาดการณ์นี้จริงนั้นค่อนข้างซับซ้อนเล็กน้อย ดังนั้นเราจะเริ่มจากการกลับไปทบทวนสมบัติบางประการของดีเทอร์มิแนนต์กันก่อน

สมบัติ 2: เพื่อความสะดวก เราจะให้สัญลักษณ์ $M(k:\vec{u})$ แทนการเขียนทับเมทริกซ์ $M$ ในหลักที่ $k$ ด้วยเวกเตอร์หลัก $\vec{u}$ (และในทำนองเดียวกัน $M(k:c) = M(k:c{\cdot}\vec{1})$ เมื่อ $c$ เป็นสเกลาร์)

1. ดึงตัวคูณสเกลาร์จากหนึ่งหลัก: $r{\cdot}\det M = \det M(k:r{\cdot}\vec{v}_k)$ สำหรับจำนวนจริง $r$ ใดๆ
2. กระจายผลบวกในหนึ่งหลัก: $\det M(k:\vec{u}{+}\vec{w}) = \det M(k:\vec{u}) + \det M(k:\vec{w})$
3. สองหลักเหมือนแล้วดีเทอร์มิแนนต์เป็นศูนย์: $\det M(i: \vec{u}, j: \vec{u}) = 0$
4. สลับสองหลักแล้วดีเทอร์มิแนนต์ติดลบ: $\det M = -\det M(i:\vec{v}_j,j:\vec{v}_i)$

บทตั้ง 3: $\det M + \det M(k:c) = \det M(k:\vec{v}_k{+}c)$

บทตั้ง 4: $\det M + \det M(i:c_i) + \det M(j:c_j) = \det M(i:\vec{v}_i{+}c_i,j:\vec{v}_j{+}c_j)$

พิสูจน์ ก่อนอื่น สังเกตว่าจากสมบัติ 2.1 และ 2.3 เรามี

\[\det M(i:c_i,j:c_j) = c_ic_j \det M(i:\vec{1},j:\vec{1}) = 0\]

ดังนั้น

\[\begin{align} &\det M + \det M(i:c_i) + \det M(j:c_j) \\ &\qquad= \det M(i:\vec{v}_i{+}c_i) + \det M(j:c_j) \\ &\qquad= \det M(i:\vec{v}_i{+}c_i) + \det M(j:c_j) + \det M(i:c_i,j:c_j) \\ &\qquad= \det M(i:\vec{v}_i{+}c_i) + \det M(i:\vec{v}_i{+}c_i,j:c_j) \\ &\qquad= \det M(i:\vec{v}_i{+}c_i,j:\vec{v}_j{+}c_j). \tag*{$\blacksquare$} \end{align}\]

ผลพลอยได้ 5: $\det M + \sum_{k\in K}\det M(k:c_k) = \det M(i:\vec{v}_k{+}c_k \mid k\in K)$ สำหรับทุกเซตดัชนี $K$

ถึงตอนนี้เราก็มีข้อมูลเพียงพอต่อการกลับไปพิสูจน์ข้อคาดการณ์ 1 แล้ว

พิสูจน์ (ของข้อคาดการณ์ 1) จากการกระจาย Laplace เราสามารถเขียนกระจายดีเทอร์มิแนนต์ให้อยู่ในรูปของผลบวกดีเทอร์มิแนนต์ที่มีมิติเล็กลงหนึ่งขั้นได้ ดังนี้

\[\det\left[\begin{array}{cccc:c} \color{red}u_1 & \color{red}u_2 & \color{red}\cdots & \color{red}u_n & \color{blue}1 \\ \hdashline v_{11} & v_{12} & \cdots & v_{1n} & 1 \\ v_{21} & v_{22} & & v_{2n} & 1 \\ \vdots & & \ddots & \vdots & \vdots \\ v_{n1} & v_{n2} & \cdots & v_{nn} & 1 \end{array}\right] = {\color{red}u_1} \det\begin{bmatrix} v_{12} & \cdots & v_{1n} & 1 \\ \vdots & \ddots & \vdots & \vdots \\ v_{n2} & \cdots & v_{nn} & 1 \end{bmatrix} - \cdots \pm {\color{blue}1} \det\begin{bmatrix} v_{11} & \cdots & v_{1n} \\ \vdots & \ddots & \vdots \\ v_{n1} & \cdots & v_{nn} \end{bmatrix}\]

สังเกตว่าแต่ละพจน์ (ยกเว้นพจน์สุดท้าย) จะมีหลักที่เป็นเวกเตอร์หนึ่งติดอยู่เสมอ เราจะสลับให้หลักนั้นไปอยู่ในหลักที่เวกเตอร์ $\vec{v}_k$ หายไป (จากการกระจายไมเนอร์) ซึ่งแต่ละพจน์ก็จะต้องสลับหลักเป็นจำนวนครั้งไม่เท่ากัน เช่น ที่พจน์รองสุดท้ายไม่ต้องสลับเลย ไล่ไปจนถึงพจน์แรกสุดที่ต้องสลับ $n{-}1$ ครั้ง เสร็จแล้วเราจะรวบพจน์ให้เหลือดีเทอร์มิแนนต์ตัวเดียว (ด้วยผลพลอยได้ 5) ซึ่งก็คือ

\[\begin{align} \det\left[\begin{array}{c:c} \color{red}\vec{u} & 1 \\ \hdashline M & \vec{1} \end{array}\right] &= (-1)^{n-1} {\color{red}u_1}\det M(1:\vec{1}) + \cdots + (-1)^{n-1} {\color{red}u_n}\det M(n:\vec{1}) + (-1)^n \det M \\ &= (-1)^n \Big( \det M(1:{\color{red}-u_1}) + \cdots + \det M(n:{\color{red}-u_n}) + \det M \Big) \\ &= (-1)^n \det M(k:\vec{v}_k{\color{red}-u_k} \mid k \in \lbrace 1,\cdots,n \rbrace) \\ &= (-1)^n \det\begin{bmatrix} v_{11}{\color{red}-u_1} & v_{12}{\color{red}-u_2} & \cdots & v_{1n}{\color{red}-u_n} \\ v_{21}{\color{red}-u_1} & v_{22}{\color{red}-u_2} & & v_{2n}{\color{red}-u_n} \\ \vdots & & \ddots & \vdots \\ v_{n1}{\color{red}-u_1} & v_{n2}{\color{red}-u_2} & \cdots & v_{nn}{\color{red}-u_n} \end{bmatrix} \end{align}\]

สังเกตว่าทุกหลักในเมทริกซ์นั้นเขียนว่า $\vec{v}_{k}{\color{red}-u_k}$ ทั้งที่ข้อคาดการณ์ที่เราอยากได้คือ ${\color{red}u_k}{-}\vec{v}_k$ ตรงนี้แก้ได้ง่ายๆ แค่กระจาย $(-1)^n$ จากนอกดีเทอร์มิแนนต์เข้าไปในแต่ละแถวนั่นเอง ซ.ต.พ.